
令和4年度上期 機械科目 問8 電験3種過去問
問題

考え方
単相変圧器の短絡試験に関する問題である。回路図を書いて考えることで、問題の内容を整理できる。そのため、回路図を書いて考えていく。短絡試験の回路は、図1に示すような回路になる。
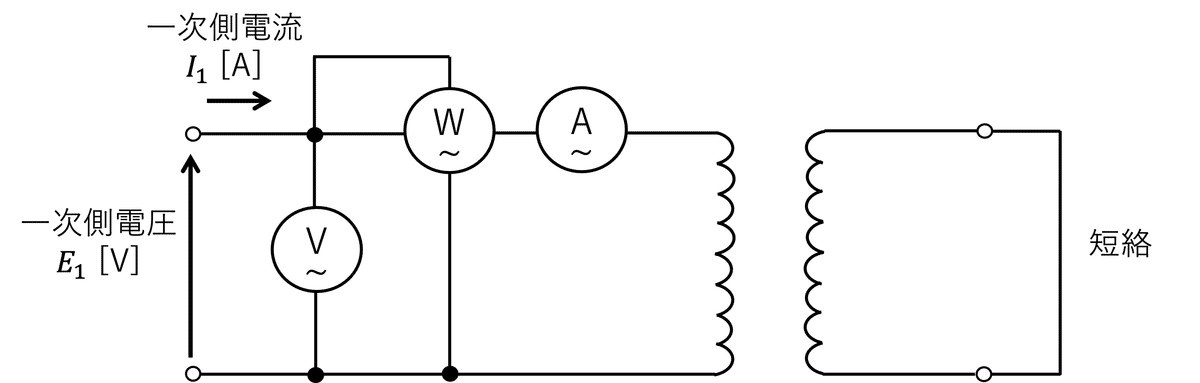
解答例
問題文で励磁回路は無視、および計器が理想的であるとしているので、図1のL型等価回路は、図2のようになる。

図2より、一次側端子からみた合成インピーダンス$${\dot{Z}_{0}}$$は、
$$
\dot{Z_{0}} = \left(R_{1}+a^{2}R_{2}\right)+j\left(x_{1}+a^{2}x_{2}\right)\tag{1}
$$
となる。また、合成インピーダンス$${\dot{Z}_{0}}$$の大きさ$${Z_{0}}$$は、
$$
Z_{0} = \sqrt{\left(R_{1}+a^{2}R_{2}\right)^{2}+\left(x_{1}+a^{2}x_{2}\right)^{2}}\tag{2}
$$
となる。短絡試験の結果から、合成インピーダンスの大きさ$${Z_{0}}$$は、
$$
Z_{0} = \frac{E_{1}}{I_{1}} = \frac{80}{40} = 2 \,{\rm{Ω}} \tag{3}
$$
と求まる。また、電力計が計測している電力は、一次巻線抵抗$${R_{1}}$$と一次側に換算した二次巻線抵抗$${a^{2}R_{2}}$$の合計なので、
$$
\begin{align}
\left(R_{1}+a^{2}R_{2}\right) &= \frac{P_{1}}{{I_{1}}^{2}} \notag\\
&= \frac{1000}{40^2} = 0.625 \,{\rm{Ω}} \tag{4}
\end{align}
$$
よって、一次側から見た漏れリアクタンス$${\left(x_{1}+a^{2}x_{2}\right)}$$は、式(2)より、
$$
\begin{align}
{Z_{0}}^{2} &=\left(R_{1}+a^{2}R_{2}\right)^{2}+\left(x_{1}+a^{2}x_{2}\right)^{2}\notag\\
2^{2}&= 0.625^{2}+\left(x_{1}+a^{2}x_{2}\right)^{2} \notag\\
\left(x_{1}+a^{2}x_{2}\right) &= \sqrt{4-0.625^{2}} = 1.90 \,{\rm{Ω}} \tag{5}
\end{align}
$$
となる。よって答えは(3)である。
関連記事
電験三種機械科目等価回路まとめ
https://note.com/elemag/n/n18cc2be15e6a?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
