
ニューラルネットワーク 単純モデル
ニューラルネットワークとは
ニューラルネットワークは、人間の脳の神経細胞(ニューロン)の構造と機能を模倣して設計されたアルゴリズムである。
人間の脳は物事を認識し、情報処理を行うことができる。これを再現することができれば、ファイルの内容を要約したり、資料を作成してくれたり、画像の加工を行ってくれたりといったことが可能となる。
単純モデル
人間の脳は、ニューロンと呼ばれる神経細胞によって情報を伝達しており、ニューロンの役目は、他のニューロンから受け取った電気信号を自分の中で計算し、次のニューロンに電気信号として送ることである。
図1のような場合を考える。

図1において、〇印で表しているものがニューロンである。また、矢印は電気信号を表す。
図1では入力が2つの場合を考えている。
左側のニューロンは入力$${x_{1},x_{2}}$$をそれぞれ受け取り、そのまま次のニューロンに伝達している。
右側のニューロンは、左側のニューロンが出力したものをそのまま受け取るのではなく、それぞれの入力に対して重みを付けている。
図1の場合、入力$${x_{1}}$$の方には、$${w_{1}}$$、入力$${x_{2}}$$の方には、$${w_{2}}$$の重みがついている。
重みは、ニューロン間の結合の強さを表すためのパラメータである。
したがって、右側のニューロンが受け取る電気信号は
$$
w_{1}x_{1}+w_{2}x_{2}
$$
となる。
電気回路において、情報は$${0}$$か$${1}$$で表現される。
図2の電気回路を考える。

図2において、電球の光が情報であるとする。
スイッチを入れていないとき、回路が繋がっていないため、電球は光らない。この状態を$${0}$$とする。
次にスイッチを入れたとき、回路が繋がるため、電球が光る。この状態を$${1}$$として表現する。
このように$${0}$$と$${1}$$で表現するものを2進数という。
つまり、図2の回路では、電球が光るか光らないの2つの状態(情報)を持つことができる。
電球の明るさを半分にすれば3つの状態を持つことができるが、スイッチだけでは明るさを半分にすることができない。また、「明るさが半分」という程度を確実に判断することは難しい。
そのため、回路の構成が簡単で、情報の判別がしやすい2進数が使用される。コンピュータの中においても、情報は$${0}$$か$${1}$$でやり取りされている。
図1に話を戻す。
右側のニューロンが$${0}$$か$${1}$$のどちらの出力を出すかは、出力信号の閾値$${\theta}$$を決めればよい。閾値以上になると$${1}$$を出力するとすれば、図1の単純モデルの出力信号$${y}$$は、
$$
y=
\begin{cases}
\,1 & (w_{1}x_{1}+w_{2}x_{2} \geq \theta)\\
\,0 &(w_{1}x_{1}+w_{2}x_{2} < \theta)
\end{cases} \tag{1}
$$
となる。
論理回路を学習してみる
実際に出力が$${0}$$か$${1}$$のみの論理回路をこの単純モデルによって学習してみる。
ニューラルネットワークが論理回路を学習するには式(1)において、$${w_{1},\, w_{2},\, \theta}$$の3つを決めることができればよい。
では、どのようにして3つのパラメータを決めるのか。
1つの方法として、適当な入力を与え、その時にモデルが出力した値と、正解の出力の値を比較し、値が違えば重みや閾値を調整していくやり方がある。これを誤り訂正学習法という。
正解の出力を$${t}$$、モデルの出力を$${y}$$とすると、以下のように修正を行っていく。
・モデルが正解の出力と同じ値を出したとき($${t=y}$$)
正しい出力を出しているので修正をしない。
・モデルの出力が正解の出力よりも大きいとき($${t=0, y =1}$$)
入力が正なら、重みを小さく
入力が負なら、重みを大きくする。
閾値を大きくする。
・モデルの出力が正解の出力よりも小さいとき($${t=1, y =0}$$)
入力が正なら、重みを大きく
入力が負なら、重みを小さくする。
閾値を小さくする。
修正分を$${\Delta w_{1},\, \Delta w_{2},\, \Delta \theta}$$とし、$${k}$$回目の試行における重みと閾値を$${{w_{1}}^{(k)},\, {w_{2}}^{(k)},\, {\theta}^{(k)}}$$とすると、誤り訂正学習法の式は、
$$
\begin{align}
\Delta w_{1} &= (t-y)x_{1}\notag\\
\Delta w_{2} &= (t-y)x_{2}\notag\\
\Delta \theta &= -(t-y)\notag\\
&\notag\\
{w_{1}}^{(k+1)}&= {w_{1}}^{(k)}+\Delta w_{1} \notag\\
{w_{2}}^{(k+1)} &= {w_{2}}^{(k)}+\Delta w_{2} \notag\\
{\theta}^{(k+1)}&= {\theta}^{(k)}+\Delta \theta\notag\\
\end{align}
$$
となる。
ANDゲート
ANDゲートは、図3に示すような図記号で表される。
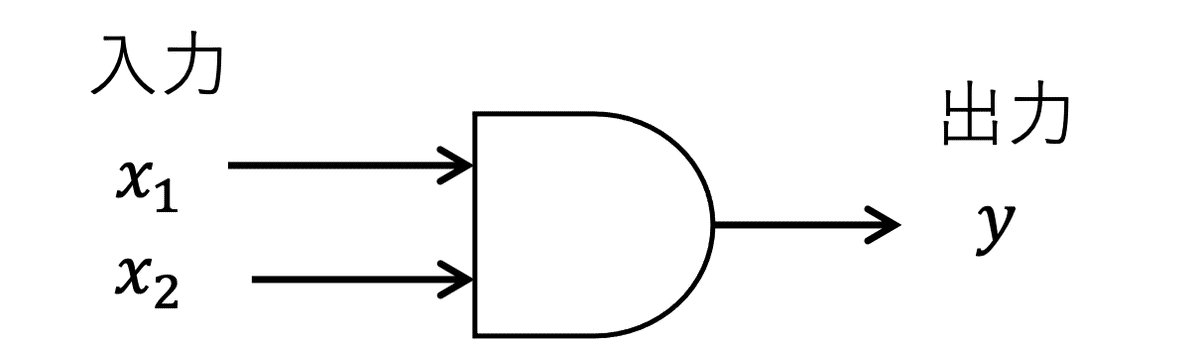
ANDゲートの動作は、図4に示すように入力がどちらも$${1}$$の場合に$${1}$$を出力し、それ以外の場合には$${0}$$を出力する。

Pythonでプログラムを作成し、学習させた結果は図5に示す通りである。プログラムについては、関連記事のANDゲート ニューラルネットワークを参照してください。

図5より誤り訂正学習法で学習させた結果、赤枠で囲った部分では、モデルがANDゲートを学習できていることがわかる。
ORゲート
ORゲートは、図6に示すような図記号で表される。

ORゲートの動作は、図7に示すように入力のどちらかが$${1}$$の場合に$${1}$$を出力し、それ以外の場合には$${0}$$を出力する。

Pythonでプログラムを作成し、学習させた結果は図8に示す通りである。プログラムについては、関連記事のORゲート ニューラルネットワークを参照してください。

図8より誤り訂正学習法で学習させた結果、赤枠で囲った部分では、モデルがORゲートを学習できていることがわかる。
NOTゲート
NOTゲートは、図9に示すような図記号で表される。

NOTゲートの動作は、入力が1つであり、図10に示すように入力が$${1}$$の場合に$${0}$$を出力し、入力が$${0}$$の場合には$${1}$$を出力する。

Pythonでプログラムを作成し、学習させた結果は図11に示す通りである。プログラムについては、関連記事のNOTゲート ニューラルネットワークを参照してください。

図11より誤り訂正学習法で学習させた結果、赤枠で囲った部分では、モデルがNOTゲートを学習できていることがわかる。
関連記事
ANDゲート ニューラルネットワーク
https://note.com/elemag/n/n3f46cb1c551c?sub_rt=share_pw
ORゲート ニューラルネットワーク
https://note.com/elemag/n/nef5db843258a?sub_rt=share_pw
NOTゲート ニューラルネットワーク
https://note.com/elemag/n/nf38706957b07?sub_rt=share_pw
参考文献
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
