
Y結線
Y結線

図1に示すような結線方式をY結線という。スター結線やワイ結線と呼ばれる。単相のものを三相交流に用いる場合に主に用いられる。特徴として、各単相の1つの端子がそれぞれ接続される。この接続点を中性点という。Y結線はベクトル図を書くことで、その特性を理解できる。今回は、単相変圧器をY結線した場合を例に見ていくが、抵抗やインピーダンスなどのY結線も特性は同じである。
Y結線のベクトル図
Y結線のベクトル図を書いていく。
図1において、$${\dot{V_{a}}}$$を基準ベクトルとする。三相交流なので、$${\dot{V_{a}}}$$、$${\dot{V_{b}}}$$、$${\dot{V_{c}}}$$は図2に示すように$${120\degree}$$の位相差を持つ。なお、相順は$${a→b→c}$$とする。

次に線間電圧$${\dot{V}_{ab}}$$を見ていく。線間電圧$${\dot{V}_{ab}}$$から見た回路は、図3に示すように相電圧$${\dot{V}_{a}}$$と相電圧$${\dot{V}_{b}}$$の2つのベクトルを足せばいいことがわかる。

したがって、線間電圧$${\dot{V}_{ab}}$$は、
$$
\dot{V}_{ab} = \dot{V}_{a} + (-\dot{V}_{b}) \tag{1}
$$
で求められる。ベクトルの足し算は矢印の方向を揃えれば良い。図3で相電圧$${\dot{V}_{b}}$$が逆方向を向いているので、マイナスをつけて図4のようにする。

式(1)の結果を図2のベクトル図に書き加えると、図5になる。まず相電圧$${\dot{V}_{b}}$$がマイナスなので、$${-\dot{V}_{b}}$$を書く、その後相電圧$${\dot{V}_{a}}$$と相電圧$${-\dot{V}_{b}}$$をベクトル合成する。その結果として得られるベクトルが線間電圧$${\dot{V}_{ab} }$$である。

ここで、相電圧$${\dot{V}_{a}}$$と線間電圧$${\dot{V}_{ab} }$$の間の角度$${\theta}$$を求める。図5にオレンジ色で示した$${\angle \alpha}$$は、$${\dot{V}_{b}}$$と$${-\dot{V}_{b}}$$がなす線分の角度が$${180\degree}$$、$${\dot{V}_{a}}$$と$${\dot{V}_{b}}$$の間の角度が$${120\degree}$$なので、
$$
\angle \alpha = 180\degree-120\degree = 60\degree \tag{2}
$$
となる。相電圧$${\dot{V}_{a}}$$と相電圧$${-\dot{V}_{b}}$$の大きさ(矢印の長さ)は等しいので、破線で示した図形はひし形になる。ひし形の半分を抜き出したものを図6に示す。ひし形の場合、対角線は図6に示すように垂直に交わる。図6は二等辺三角形であるため、底辺に垂直に交わる線は、$${\angle 60\degree}$$を2等分する。よって、$${\theta}$$は$${30\degree}$$となる。このことから、相電圧$${\dot{V}_{a}}$$と線間電圧$${\dot{V}_{ab} }$$の間には、$${30\degree}$$の位相差があることが分かる。

次にベクトルの大きさの関係をみていく。図7に直角三角形の三角比を示す。緑色の部分の大きさ$${V_{g}}$$は、青色の相電圧$${\dot{V}_{a}}$$の大きさを$${V_{a}}$$とすれば、
$$
\begin{align}
V_{a}:V_{g} &= 2:\sqrt{3} \notag \\
V_{g} &= \frac{\sqrt{3}}{2}V_{a} \tag{3}
\end{align}
$$
と求まる。$${V_{g}}$$は半分を抜き出したものであるから、線間電圧$${\dot{V}_{ab} }$$の大きさ$${V_{ab} }$$は$${V_{g}}$$を2倍すればよい。よって、
$$
V_{ab} = 2\times V_{g} = 2\times\frac{\sqrt{3}}{2}V_{a} = \sqrt{3}V_{a} \tag{4}
$$
となり、線間電圧は相電圧の$${\sqrt{3}}$$倍となっていることが分かる。

最後に他の線間電圧のベクトルも同様にして、
$$
\begin{align}
\dot{V}_{bc} &= \dot{V}_{b} + (-\dot{V}_{c}) \tag{5} \\
\dot{V}_{ca} &= \dot{V}_{c} + (-\dot{V}_{a}) \tag{6}
\end{align}
$$
の関係から、ベクトル図を書くと図8のようになる。

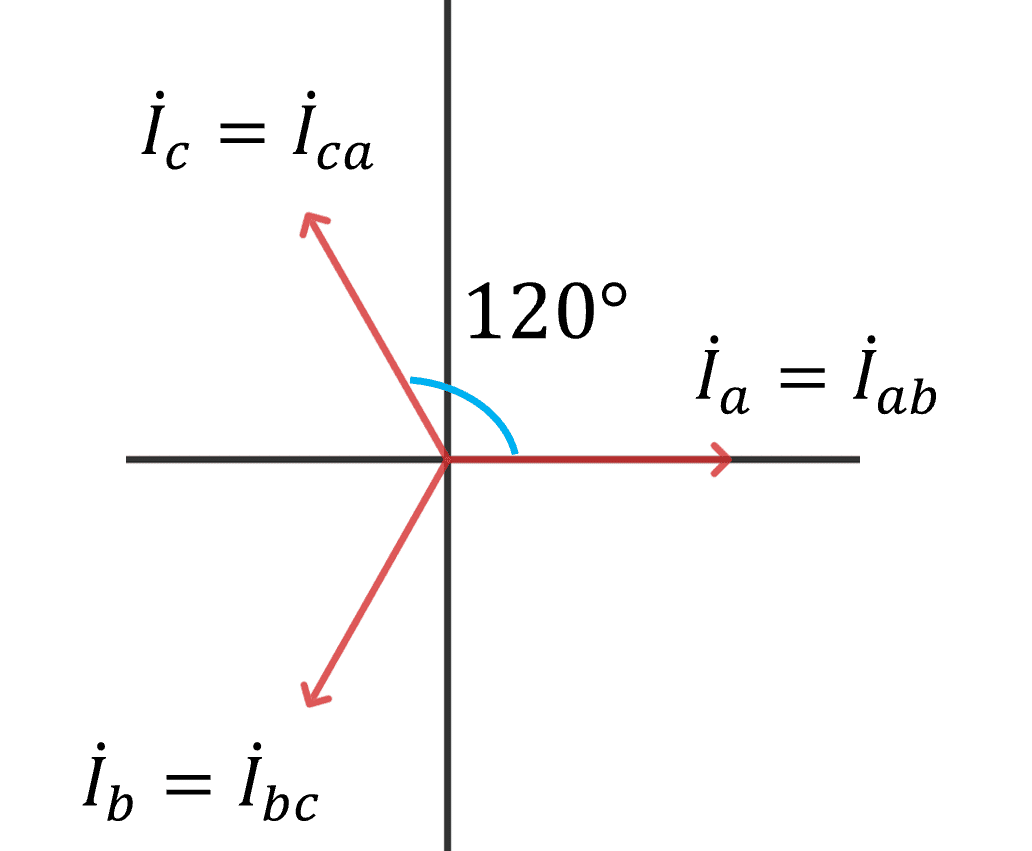
Y結線における電流は、図1より相電流と線電流は同じ電流であるため、大きさは等しい。また、三相交流なので、各相に$${120\degree}$$の位相差を持つ。そのため、図9のようになる。
相電圧と相電流を同相とした場合のベクトル図は図10(a)のようになり、線間電圧と相電流を同相とした場合のベクトル図は図(b)となる。

Y結線の相と線間の関係まとめ
最後にY結線の重要事項をまとめる。
Y結線では、相電圧と線間電圧の間に$${30\degree}$$の位相差をもつ。
相電圧を基準に見れば、線間電圧は$${30\degree}$$進んでおり、
線間電圧を基準に見れば、相電圧は$${30\degree}$$遅れている。
また、線間電圧の大きさは、相電圧の大きさの$${\sqrt{3}}$$倍である。
電流のベクトルは、相電流と線電流は大きさが等しく、位相差もない。
関連記事
Δ結線
https://note.com/preview/nbd92bde1cdcd?prev_access_key=8dc5f4d9f4833fa0e877ba64b42a0b84
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
