同期発電機の並行運転

2023年12月20日 18:44

並行運転

同期発電機を複数台並列にして、運転する方法を並行運転という。図1に2台の同期発電機で運転する場合の回路図を示す。並行運転する際には、後発投入する側(後で投入される側)は、同期を取る必要がある。

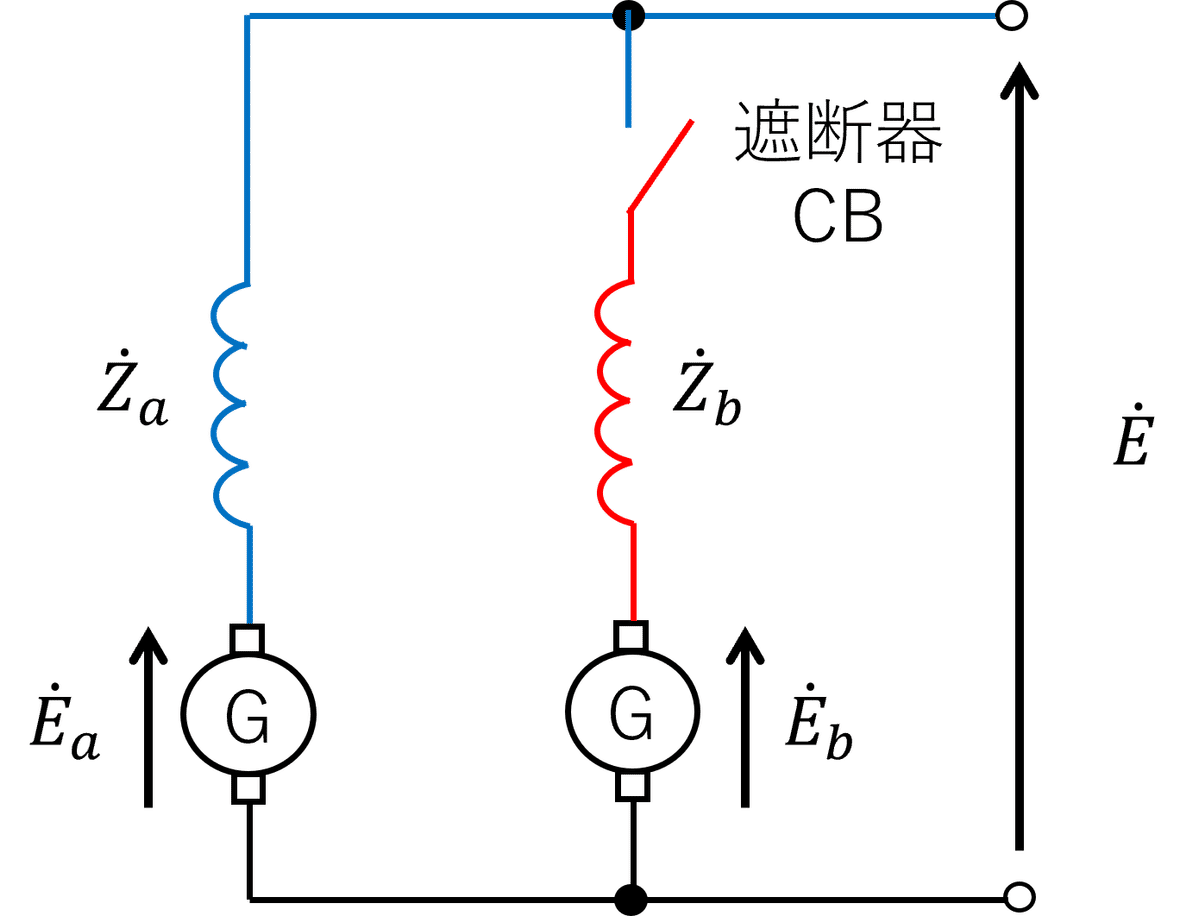
例として、図2の状況を考える。今、発電機Aが先発(先に投入される側)投入され、発電機Aのみで負荷に電力を供給している。負荷が増加し、発電機Aだけでは容量不足になるため、発電機Bを投入したい。この時、発電機Bは発電機Aが供給している電圧波形と一致するように、原動機の回転速度や励磁を調整しないといけない。この電圧波形を一致させることを同期をとるという。電圧波形が一致しないといけない理由は、後で述べる。発電機Bが同期をとれた場合のみ、遮断機CBが投入され、図1のように2台で運転することができる。図2の状況を系統図としてみると、図3のようになる。

電圧の大きさが異なる場合

並行運転する際には、後発側が同期を取らないといけない。ここからは、なぜ同期が必要かを見ていく。図4は、発電機Aと発電機Bが同期をとれた状態である。

ここで、発電機Aの電圧が発電機Bより大きい場合を図5に示す。図5では、発電機Aと発電機Bの間に、電位差が生じていることが確認できる。

発電機Aと発電機Bの間で電位差があるということは、図6に示すように、発電機間に電流が流れる。これを循環電流という。循環電流$${\dot{I_{c}}}$$は、

$$
\dot{I_{c}} = \frac{\dot{E}_{a}-\dot{E}_{b}}{\dot{Z}_{a}+\dot{Z}_{b}} \tag{1}
$$

で求まる。

循環電流は、有効分と無効分で役割が異なる。
今、電圧の大きさのみを変化させることを考える。
電圧の大きさは、$${E_{a}>E_{b}}$$、電圧の差分を$${\dot{E}_{c}}$$、インピーダンスは、電機子抵抗が十分小さいとして、$${\dot{Z}_{a}=\dot{Z}_{b}=jx_{s}}$$とすれば、循環電流$${\dot{I}_{c}}$$は、式(1)より

$$
\begin{align}
\dot{I_{c}} &= \frac{\dot{E}_{a}-\dot{E}_{b}}{\dot{Z}_{a}+\dot{Z}_{b}} \notag\\
&= \frac{\dot{E}_{c}}{j x_{s}+j x_{s}}\notag\\
&= -j\frac{\dot{E}_{c}}{2x_{s}}\tag{2}\\
\end{align}
$$

となる。

図7に電圧の大きさが異なる場合のベクトル図を示す。今変化させているのは、大きさのみであるので、ベクトルの向きは同じで、長さが異なる状況である。また、循環電流$${\dot{I}_{c}}$$は、電圧の差分$${\dot{E}_{c}}$$に対して$${\frac{\pi}{2}}$$遅れとなる。
発電機Aでは、循環電流$${\dot{I}_{c}}$$は、流れ出る方向である。よって、発電機Aの電圧より$${\frac{\pi}{2}}$$遅れの電流になる。一方で、図6に示すように、発電機Bは、循環電流$${\dot{I}_{c}}$$が流れ込んでくるので、$${-\dot{I}_{c}}$$となる。そのため、循環電流$${\dot{I}_{c}}$$は、発電機Bの電圧より$${\frac{\pi}{2}}$$進みの電流になる。発電機Aでは、減磁作用により、界磁が弱まる。発電機Bでは、増磁作用で界磁が強まるため、発電機間で誘導起電力が等しくなるように働く。この時の循環電流は、無効分であり、横流または、無効横流とよぶ。実際には、自動電圧調整器(AVR)で横流補償を行うことで、迅速に電圧の大きさが一致するように調整する。

位相差がある場合

電位差を生じさせるのは、電圧の大きさが異なるときだけではない。図8のように、位相差がある場合も電位差が生じる。

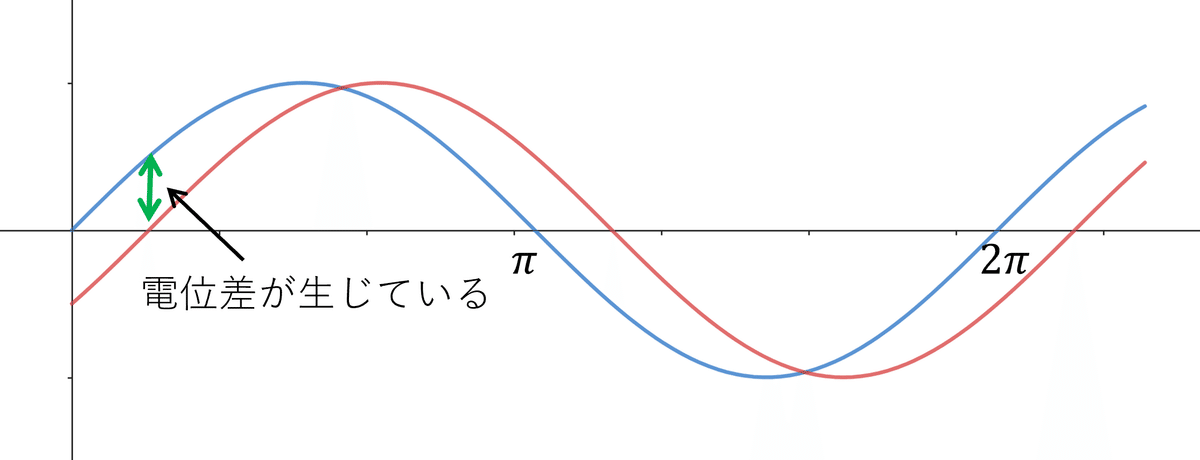
図8の状況においても、電位差が生じるため循環電流$${\dot{I}_{c}}$$が流れる。位相差が生じる場合のベクトル図は、図9のようになる。発電機Bが発電機Aより位相が$${\delta}$$だけ遅れている場合を示している。

電圧の差分を$${\dot{E}_{c}}$$、インピーダンスは、電機子抵抗が十分小さいとして、$${\dot{Z}_{a}=\dot{Z}_{b}=jx_{s}}$$とすれば、循環電流$${\dot{I}_{c}}$$は、式(2)と同様に、

$$
\begin{align}
\dot{I_{c}} &= \frac{\dot{E}_{a}-\dot{E}_{b}}{\dot{Z}_{a}+\dot{Z}_{b}} \notag\\
&= \frac{\dot{E}_{c}}{j x_{s}+j x_{s}}\notag\\
&= -j\frac{\dot{E}_{c}}{2x_{s}}\tag{3}\\
\end{align}
$$

となり、$${\dot{E}_{c}}$$に対して$${\frac{\pi}{2}}$$遅れとなるので、図10のようになる。

ここで、図11に示すように、電圧の差分ベクトル$${\dot{E}_{c}}$$と循環電流$${\dot{I}_{c}}$$を原点に移動させる。

原点に移動させると、図12のベクトル図ができる。

発電機電圧$${\dot{E}_{a}}$$、$${\dot{E}_{b}}$$の電圧の大きさを$${E_{0}}$$とすれば、図13のような二等辺三角形ができることが分かる。電圧の差分ベクトル$${\dot{E}_{c}}$$と循環電流$${\dot{I}_{c}}$$が、直角に交わることは、図10で見た通りである。

二等辺三角形の性質の1つとして、二等辺三角形の頂角の二等分線は底辺と直角に交わるというものがある。循環電流$${\dot{I}_{c}}$$は、頂角から出て、底辺と直角に交わっているため、循環電流$${\dot{I}_{c}}$$の線分は、二等分線となっている。よって、図14のように循環電流$${\dot{I}_{c}}$$と各発電機電圧の間には、$${\frac{\delta}{2}}$$の位相差がある。

循環電流$${\dot{I}_{c}}$$によって、発生する電力を考える。
電圧の差分ベクトル$${\dot{E}_{c}}$$は、図9と図14から、$${\dot{E}_{a}}$$の$${\sin}$$成分を2倍すれば良い。発電機Aの電圧$${\dot{E}_{a}}$$の大きさは$${E_{0}}$$なので、

$$
\dot{E}_{c} = j2E_{o}\sin\left(\frac{\delta}{2}\right)\tag{4}
$$

となる。よって、式(3)で求めた循環電流$${\dot{I}_{c}}$$は、

$$
\begin{align}
\dot{I_{c}} &= -j\frac{\dot{E}_{c}}{2x_{s}}\notag\\
&=-j\frac{\left(j2E_{o}\sin\left(\frac{\delta}{2}\right)\right)}{2x_{s}}\notag\\
&= \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\tag{5}
\end{align}
$$

となる。これは、電圧の大きさが異なるときの循環電流と異なり、有効分の電流となっている。
循環電流$${\dot{I}_{c}}$$によって、各発電機で発生する電力$${P}$$は、

発電機A
発電機Aの電圧$${\dot{E}_{a}}$$の大きさは$${E_{0}}$$、循環電流$${\dot{I}_{c}}$$の大きさは、$${\frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)}$$なので、

$$
\begin{align}
P_{A}&= E_{0}I_{c}\cos\left(\frac{\delta}{2}\right)\notag\\
&= E_{0} \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left(\frac{\delta}{2}\right)\tag{6}\\
\end{align}
$$

ここで、加法定理より、

$$
\begin{align}
\sin(a+b)&= \sin(a)\cos(b)+\cos(a)\sin(b) \tag{7}\\
\sin(a-b)&= \sin(a)\cos(b)-\cos(a)\sin(b) \tag{8}\\
\end{align}
$$

であるが、式(7)と式(8)を足すと、

$$
\begin{align}
\sin(a+b)+\sin(a-b)&= 2\sin(a)\cos(b)\notag\\
\sin(a)\cos(b) &= \frac{\sin(a+b)+\sin(a-b)}{2}\notag\\
\sin\left(\frac{\delta}{2}\right)\cos\left(\frac{\delta}{2}\right) &= \frac{\sin\left(\frac{\delta}{2}+\frac{\delta}{2}\right)+\sin\left(\frac{\delta}{2}-\frac{\delta}{2}\right)}{2}\notag\\
&= \frac{\sin\left(\delta\right)}{2} \tag{9}
\end{align}
$$

となる。式(9)を式(6)に代入すると、

$$
\begin{align}
P_{A}&= E_{0} \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left(\frac{\delta}{2}\right)\notag\\
&= \frac{{E_{0}}^{2}}{x_{s}}\frac{\sin\left(\delta\right)}{2} \notag\\
&= \frac{{E_{0}}^{2}}{2x_{s}}\sin\left(\delta\right)\tag{10}
\end{align}
$$

となり、これが循環電流$${\dot{I}_{c}}$$によって、発電機Aで発生する電力である。

発電機B

発電機Bは、循環電流$${\dot{I}_{c}}$$が流れ込むので、$${-\dot{I}_{c}}$$となる。図15に示すように$${-\dot{I}_{c}}$$は、発電機Bの電圧$${\dot{E}_{b}}$$と$${\left(\pi - \frac{\delta}{2}\right)}$$の位相差がある。よって、循環電流$${\dot{I}_{c}}$$によって、発電機Bに発生する電力$${P_{B}}$$は、発電機Bの電圧$${\dot{E}_{b}}$$の大きさが$${E_{0}}$$、循環電流$${\dot{I}_{c}}$$の大きさが、$${\frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)}$$なので、

$$
\begin{align}
P_{B}&= E_{0}I_{c}\cos\left(\pi - \frac{\delta}{2}\right)\notag\\
&= E_{0} \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left(\pi - \frac{\delta}{2}\right)\tag{11}\\
\end{align}
$$

となる。$${\cos\left(\pi - \frac{\delta}{2}\right)}$$は、加法定理より

$$
\begin{align}
\cos\left(\pi - \frac{\delta}{2}\right) &= \cos(\pi)\cos\left( \frac{\delta}{2}\right)+\sin(\pi)\sin \left( \frac{\delta}{2}\right)\notag\\
&= -\cos\left( \frac{\delta}{2}\right)\tag{12}
\end{align}
$$

となるので、式(11)は、

$$
\begin{align}
P_{B} &= E_{0} \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left(\pi - \frac{\delta}{2}\right)\notag\\
&= E_{0} \frac{E_{0}}{x_{s}}\sin\left(\frac{\delta}{2}\right) \left(-\cos\left( \frac{\delta}{2}\right)\right)\notag\\
&= - \frac{{E_{0}}^{2}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left( \frac{\delta}{2}\right)\tag{13}
\end{align}
$$

となるが、式(13)は、式(6)にマイナスを掛けただけなので、

$$
\begin{align}
P_{B} &= - \frac{{E_{0}}^{2}}{x_{s}}\sin\left(\frac{\delta}{2}\right)\cos\left( \frac{\delta}{2}\right)=-P_{A}\tag{14}
\end{align}
$$

となる。

よって、循環電流によって、発電機Aでは、$${P_{A}}$$だけ電力が増えるので、速度が遅れる。発電機Bでは、$${P_{A}}$$だけ電力が減るので、速度が増加する。したがって、この有効分の循環電流は、発電機間の速度を一致させるように働き、電圧の位相を保つように働く。この時の電流を同期化電流という。