
令和5年度上期 機械科目 問13 電験3種過去問
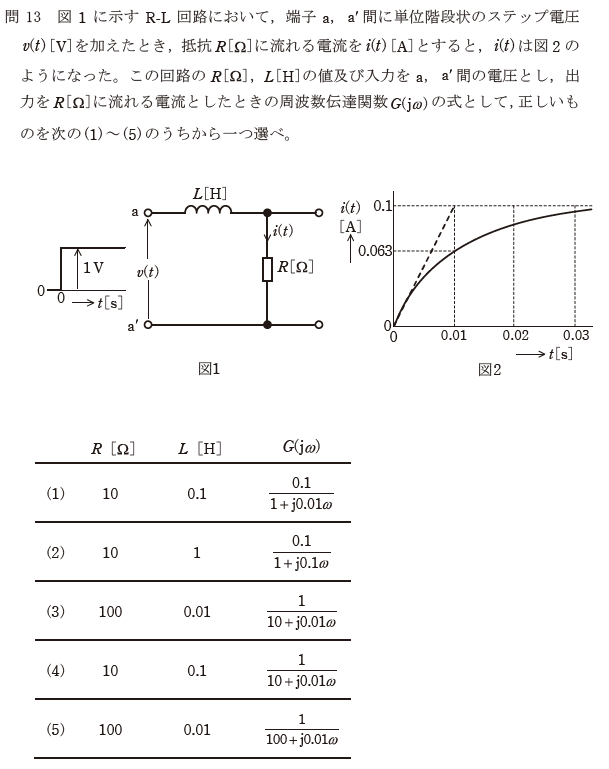
問題
考え方
この問題は、制御工学を学ぶとよく出てくる伝達関数についての問題である。周波数伝達関数は、$${s}$$領域の伝達関数$${G(s)}$$を周波数領域$${j\omega}$$で考えたものである。そのため、まずは$${s}$$領域の伝達関数$${G(s)}$$を求める。
解答例
問題文で入力とされている$${a,a^\prime}$$間の電圧$${v(t)}$$は、
$$
v(t) = L\frac{{\rm{d}}}{{\rm{d}}t}i(t)+Ri(t) \tag{1}
$$
である。電流の初期値は、問題のグラフから0である。よって、式(1)をラプラス変換すると、
$$
\begin{align}
\mathcal{L}\left[v(t)\right] &= \mathcal{L}\left[L\frac{{\rm{d}}}{{\rm{d}}t}i(t)+Ri(t)\right] \notag\\
V(s) &= LsI(s)+RI(s) \tag{2}
\end{align}
$$
となる。出力は、電流$${I(s)}$$である。式(2)を変形すると、
$$
\begin{align}
V(s) &= LsI(s)+RI(s) \notag\\
V(s) &= \left(Ls+R\right)I(s) \notag\\
\frac{I(s)}{V(s)} &=\frac{1}{\left(Ls+R\right)} \tag{3}
\end{align}
$$
となるので、1次遅れ伝達関数$${G(s)}$$の標準形
$$
G(s) = \frac{K}{Ts+1} \tag{4}
$$
$${T}$$:時定数、$${K}$$:ゲイン
に、変形すると、
$$
\begin{align}
G(s) = \frac{I(s)}{V(s)} &= \frac{1}{\left(Ls+R\right)} \notag\\
&= \frac{1}{\left(Ls+R\right)} \times \frac{\frac{1}{R}}{\frac{1}{R}} \notag\\
&= \frac{\frac{1}{R}}{\left(\frac{L}{R}s+1\right)} \tag{5}
\end{align}
$$
と求まる。時間$${t}$$が$${t= T}$$となるとき、出力の大きさが、$${63.2\%}$$になる。問題のグラフから、出力の大きさが$${63.2\%}$$の時の時間は、$${0.01}$$である。これより、
$$
\frac{L}{R} = 0.01 \tag{6}
$$
の関係が成り立つ。また、問題のグラフの最終値は、入力したステップ電圧とゲイン$${K}$$の積になる。ステップ電圧の大きさが$${1}$$、グラフの最終値は$${0.1}$$であるから、
$$
\frac{1}{R} = 0.1 \tag{7}
$$
の関係が成り立つ。よって、式(6)および式(7)から、$${R=10}$$、$${L=0.1}$$と求まる。また、周波数伝達関数$${G(j\omega)}$$は、式(5)の$${s}$$を$${j\omega}$$に置き換えたものであるから、
$$
G(j\omega)= \frac{\frac{1}{R}}{\left(j\frac{L}{R}\omega+1\right)} \tag{8}
$$
となり、式(6)および式(7)の値を代入すると、
$$
G(j\omega)= \frac{0.1}{\left(1+j0.01\omega\right)} \tag{9}
$$
と求まる。よって、答えは、(1)である。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
