
等価回路でみる直流発電機
直流発電機の直巻、分巻、他励の3種類について、等価回路から読み取れることをみていく。式はもちろんのこと、式から読み取れることも多くある。等価回路を理解して、暗記を減らしましょう。
定義されている式
誘導起電力$${E}$$
$$
E = \frac{p}{a}Z \Phi \frac{N}{60} = K_{g}\Phi N \tag{1}
$$
$${p}$$:極数 $${a}$$:並列回路数
$${Z}$$:電機子導体数 $${\Phi}$$:毎極の磁束
$${N}$$:回転速度
直巻発電機の等価回路

図1に示した直巻発電機の等価回路から導かれる式をみていく。
電流の関係
直巻の場合、電機子電流$${I_{a}}$$、界磁電流$${I_{f}}$$、負荷電流$${I}$$は、図1から明らかなように、次式が成り立つ。
$$
I_{a} = I_{f} = I \tag{2}
$$
端子電圧$${V}$$
$$
\begin{align}
V &= E-R_{a}I_{a} - R_{f}I_{f} - v_{b} \notag \\
&= E-\left(R_{a}+R_{f}\right)I -v_{b}\tag{3}
\end{align}
$$
分巻発電機の等価回路

電流の関係
分巻の場合、電機子電流$${I_{a}}$$、界磁電流$${I_{f}}$$、負荷電流$${I}$$は、図2から次式が成り立つ。
$$
\begin{align}
I_{a} &= I_{f} + I \tag{4} \\
I_{a} &\propto I \tag{5}
\end{align}
$$
界磁抵抗$${R_{f}}$$を変化させないとき、界磁電流$${I_{f}}$$は変化しないので、式(4)において、負荷電流と電機子電流は比例する。
端子電圧$${V}$$
$$
\begin{align}
V &= R_{f}I_{f}\tag{6} \\
&= E-R_{a}I_{a} -v_{b}\tag{7}
\end{align}
$$
他励発電機の等価回路
電流の関係
他励の場合、界磁電流$${I_{f}}$$は外部電源から作られる。電機子電流$${I_{a}}$$と負荷電流$${I}$$は、図3から次式が成り立つ。
$$
I_{a} =I \tag{8}
$$
端子電圧$${V}$$
$$
\begin{align}
V &= E-R_{a}I -v_{b} \tag{9} \\
\end{align}
$$
界磁電圧$${V_{f}}$$
$$
V_{f} = R_{f}I_{f} \tag{10}
$$
各式から読み取れること
無負荷飽和曲線
無負荷飽和曲線とは、定格回転数を保ちながら、無負荷運転した時の界磁電流と誘導起電力との関係を表すものである。
直巻は界磁電流と負荷電流が等しいので、負荷電流により常に端子電圧および誘導起電力が変化する。そのため、発電機には向いていない。よって、無負荷飽和曲線を考えても実用的でない。
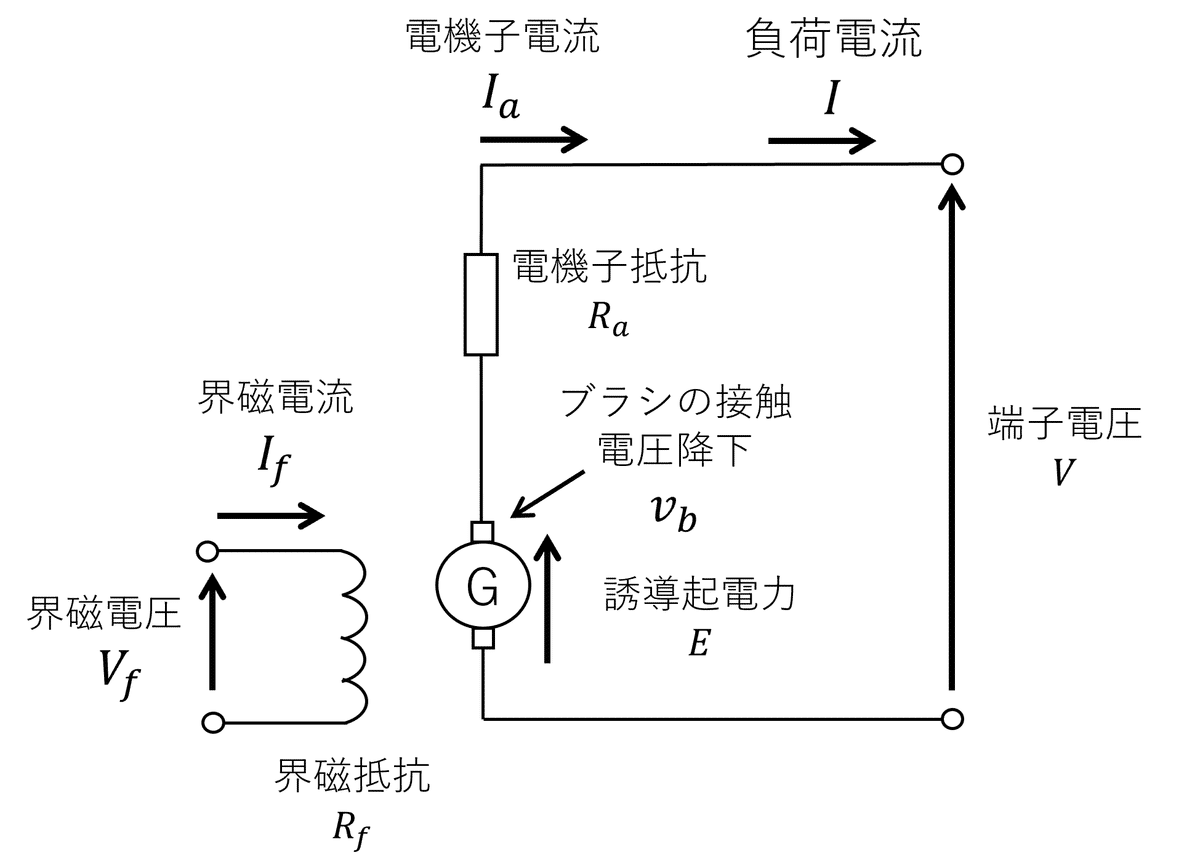
他励の場合、図3より界磁電流は外部電源で調整できる。また、式(1)より、誘導起電力は回転数一定であれば、界磁磁束に比例する。界磁磁束は界磁電流に比例するので、誘導起電力は界磁電流に比例する。よって、図4に示すように界磁電流に比例して、誘導起電力は増加する。界磁電流は無限に増加するわけではない。界磁鉄心の磁気飽和により、界磁磁束が増加しにくくなる。そのため、磁気飽和が始まると、誘導起電力の増加も緩やかになっていく。また、誘導起電力は界磁鉄心の残留磁束により、必ず回転させると残留電圧を発生する。
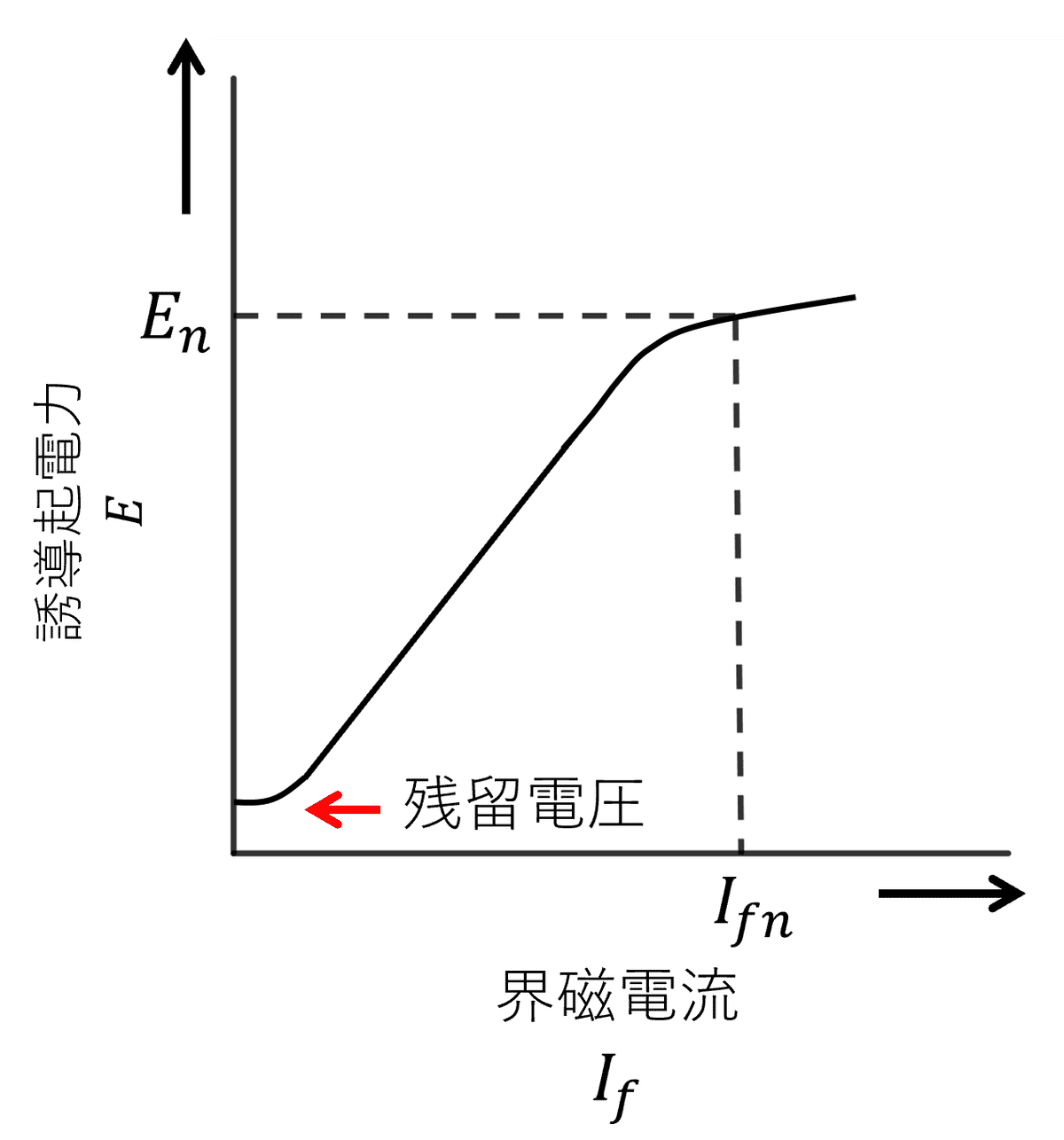
界磁電流を増加させ、その後減少させると、図5に示すようにヒステリシス特性を示す。そのため、無負荷飽和特性試験をする際には、界磁電流を上げ下げせずに、一方向のみに界磁電流を操作することが必要である。
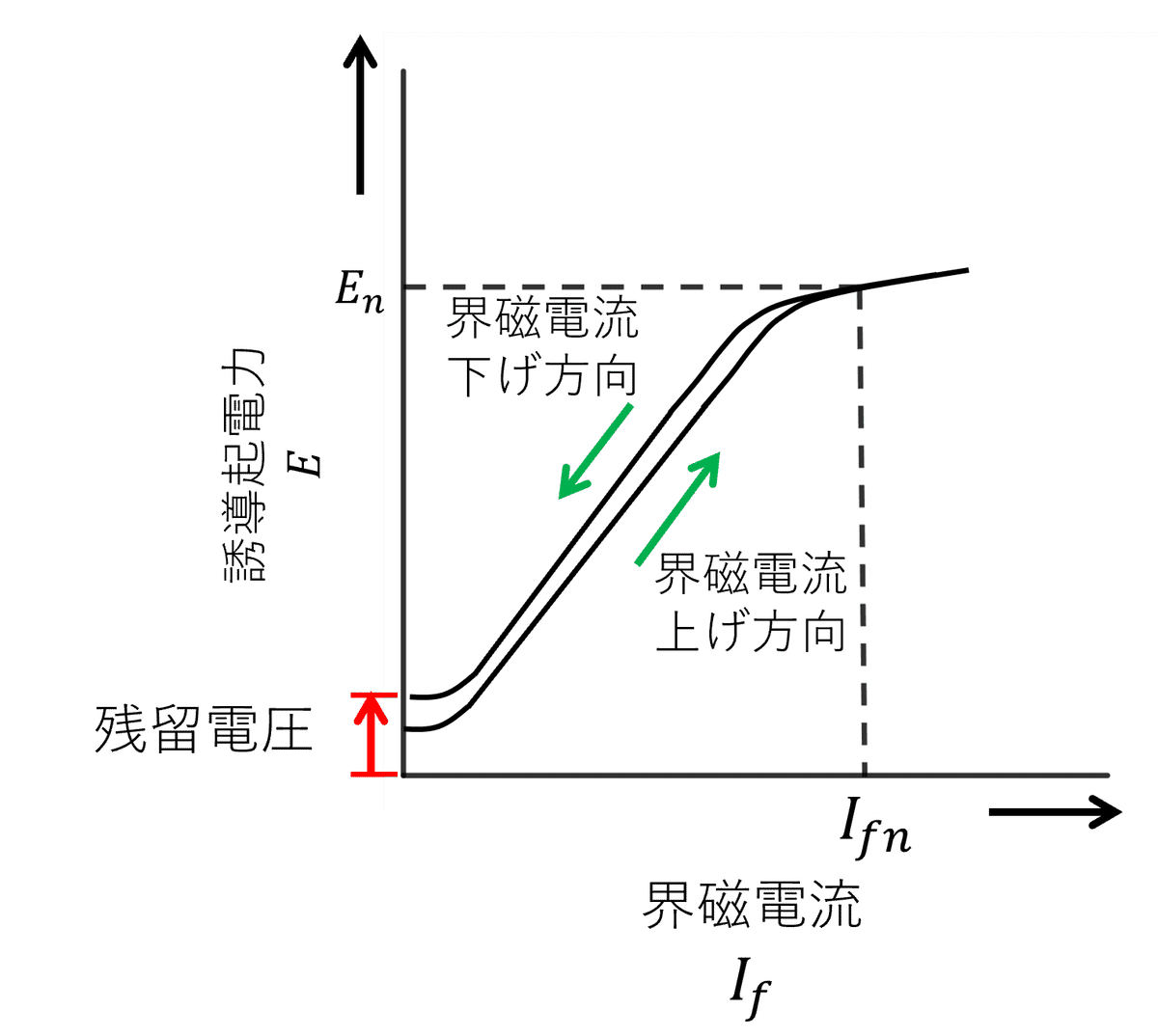
分巻の場合は、発電機電圧が発生しないと界磁電流が流れない。しかし、残留磁束が存在しているため、発電機を回転させることで、式(1)から誘導起電力は発生する。図6に示すように、誘導起電力が発生すれば、界磁電流が流増加する。界磁電流が増加すると、さらに誘導起電力が増加する。このサイクルを繰り返すことで、定格電圧まで上昇していく。誘導起電力は無限に上昇するわけではなく、界磁鉄心の磁気飽和により、界磁磁束が増加しにくくなる。そのため、無負荷飽和曲線と界磁抵抗線$${R_{f}I_{f}}$$の交点で安定した電圧になる。

外部特性曲線
外部特性曲線とは、定格回転数で運転した時の端子電圧と負荷電流の関係を表すものである。
直巻は、界磁電流と負荷電流が等しいので、負荷電流により常に端子電圧および誘導起電力が変化する。そのため、発電機には向いていない。よって、外部特性曲線を考えても実用的でない。
他励の式(9)は、端子電圧を表す式である。ブラシの接触電圧降下$${v_{b}}$$および誘導起電力$${E}$$は一定とすると、負荷電流$${I}$$の増加に対して、端子電圧$${V}$$は図7のように低下することがわかる。

分巻の端子電圧を表す式(7)において、ブラシの接触電圧降下$${v_{b}}$$および誘導起電力$${E}$$は一定とすると、端子電圧$${V}$$は電機子電流$${I_{a}}$$に比例する。また電機子電流$${I_{a}}$$は、式(5)より$${I_{a} \propto I }$$であるから、端子電圧は負荷電流に比例する。図8に示すように負荷電流が増加すると、出力できる電力は同じであるため、端子電圧が低下する。これに伴って、式(6)から界磁電流も低下する。界磁電流が低下すると、式(1)から誘導起電力も低下するため、分巻発電機の端子電圧は、他励に比べて端子電圧の低下は大きくなる。また、定格電流以上に負荷電流が大きくなると、端子電圧の低下と界磁電流の低下がさらに進み、ある限界点を示す。限界点以降は、電流が減少し、最終的には、$${I_{s0}}$$になる。この電流は、残留電圧で流れる短絡電流である。

関連記事
電験3種機械科目等価回路まとめ
https://note.com/elemag/n/n18cc2be15e6a
等価回路でみる三相誘導電動機
https://note.com/elemag/n/n1453fa715769?sub_rt=share_pw
等価回路でみる直流電動機
https://note.com/elemag/n/n28872c3b3273?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
この記事が気に入ったらサポートをしてみませんか?
