令和4年度下期　機械科目　問5　電験3種過去問

2023年12月5日 17:28

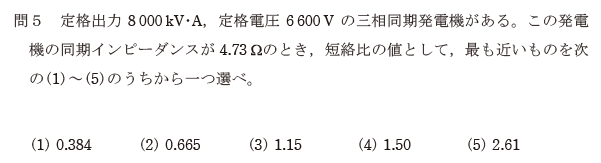
問題

この問題は短絡比を求める問題だが、短絡比を求める式は、

$$
\begin{align}
\rm{k} &= \frac{1}{\%z \,[\rm{p.u.}]} \tag{1}\\
\rm{k} &= \frac{I_{\rm{s}}}{I_{\rm{n}}} \tag{2}
\end{align}
$$

の2通りがある。今回与えられている情報では、短絡電流$${I_{\rm{s}}}$$は求めようがないため、式(1)を用いるしかない。そのため、百分率インピーダンス$${\%z}$$を求めていく。

百分率インピーダンスは、定格電圧$${\rm{V_{n}}}$$、定格容量$${\rm{P_{n}}}$$、同期インピーダンス$${Z}$$とすれば、次式で求まる。

$$
\%z = \frac{\rm{P_{n}}Z}{\rm{V_{n}}^{2}} \times 100 \quad [\%] \tag{3}
$$

式(3)より、

$$
\%z = \frac{8000\times10^{3}\times4.73}{6600^{2}} \times 100 = 86.87 \% \tag{4}
$$

よって、短絡比$${\rm{k}}$$は、式(4)の結果を単位法に戻して、式(1)に代入すると、

$$
\rm{k} = \frac{1}{\%z \,[p.u.]} = \frac{1}{0.8687} = 1.15 \tag{5}
$$

となり、答えは(3)となる。