
交流回路のベクトル図
交流回路の表し方
交流を表す方法の1つとして、複素平面上にベクトルを取り、複素数で表す方法がある。これを複素数表示という。

図1のベクトル$${\dot{E}}$$は、実部を$${E_{\rm{R}}}$$、虚部を$${jE_{\rm{i}}}$$とすれば、
$$
\dot{E} = E_{\rm{R}}+jE_{\rm{i}} \tag{1}
$$
と表せる。ベクトル$${\dot{E}}$$の大きさを$${E}$$、位相角を$${\theta}$$とすれば、
$$
\dot{E} = E\angle \theta \tag{2}
$$
と表す方法もある。これを極座標表示、またはフェーザ表示という。極座標表示の場合、位相角$${\theta}$$の単位は[$${\degree}$$]である。
ベクトル$${\dot{E}}$$の実部$${E_{\rm{R}}}$$、虚部$${jE_{\rm{i}}}$$はそれぞれ、
$$
\begin{align}
E_{\rm{R}} &= E\cos(\theta) \tag{3} \\
jE_{\rm{i}} &= jE\sin(\theta) \tag{4}
\end{align}
$$
で求めることができるから、式(1)は、
$$
\begin{align}
\dot{E} &= E\cos(\theta)+ jE\sin(\theta)\notag \\
&= E\left(\cos(\theta)+ j\sin(\theta)\right) \tag{5}
\end{align}
$$
とも表すことができ、オイラーの公式を用いれば、
$$
\dot{E} = Ee^{j\theta} \tag{6}
$$
となる。
基本要素のベクトル図
電気回路の基本素子としては、抵抗、コイル、コンデンサの3つがある。まずは、これら基本素子のベクトル図を見ていき、その後にそれぞれを組み合わせた場合を見ていく。また、交流回路のベクトル図は、フェーザ図と言われることもある。
抵抗

図2に示すように抵抗のみの回路における電圧$${\dot{V}}$$、電流$${\dot{I}}$$を考える。
電圧と電流の関係は、
$$
\dot{V} = R\,\dot{I} \tag{7}
$$
であるから、電圧と電流は同相である。よって、ベクトル図は電圧を基準とすると、図3のようになる。

コイル

図4に示したコイルのみの回路を考える。電圧と電流の関係は、
$$
\dot{V} = j\omega L\,\dot{I} \tag{8}
$$
である。ここで$${j}$$は、指数関数表示すると、
$$
e^{j\frac{\pi}{2}} = \cos\left(\frac{\pi}{2}\right)+j\sin\left(\frac{\pi}{2}\right) = j \tag{9}
$$
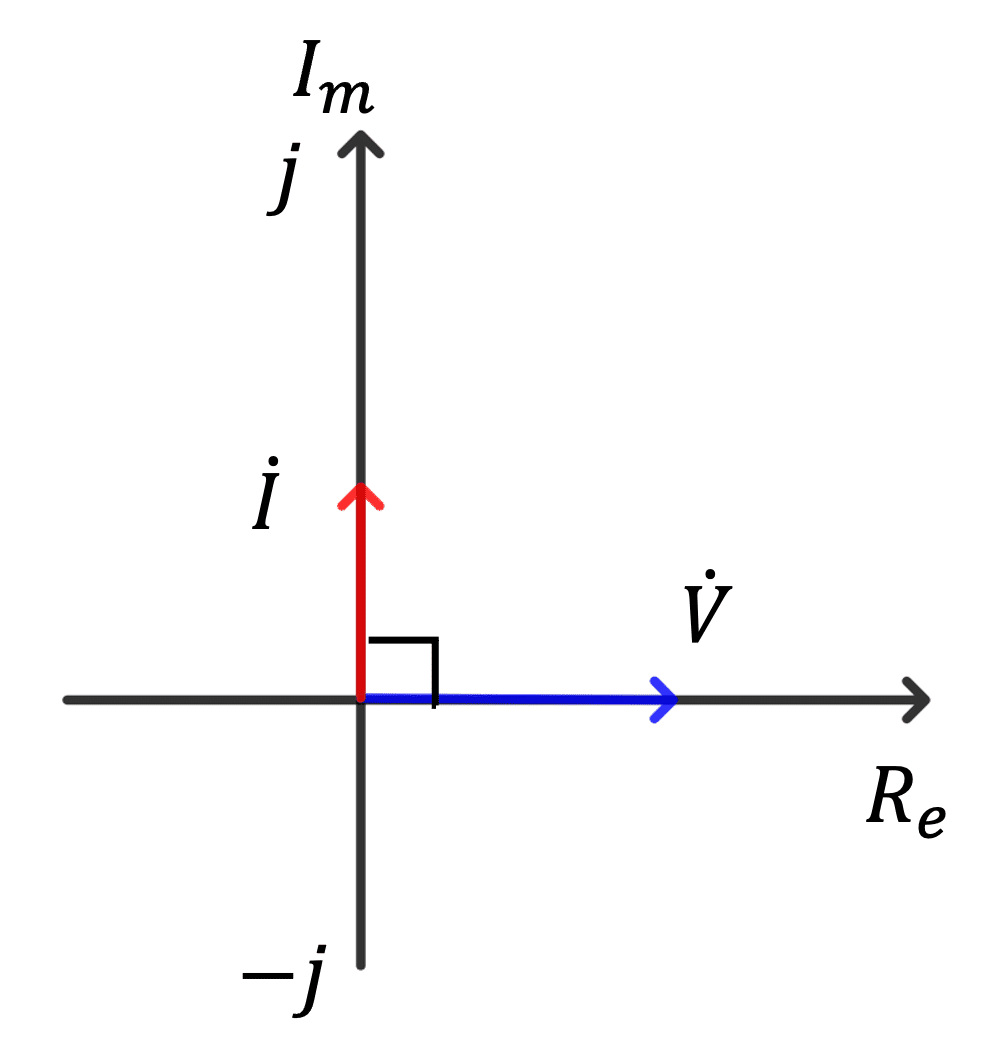
より、位相を$${90\degree}$$進める働きを持っている。よって、式(8)より、コイルの電圧$${\dot{V}}$$は、電流$${\dot{I}}$$より$${90\degree}$$進んでいる。電圧ベクトルを基準にすると、電流は$${90\degree}$$遅れるので、ベクトル図は、図5のようになる。

コンデンサ

図6に示したコンデンサのみの回路を考える。電圧と電流の関係は、
$$
\begin{align}
\dot{V} &= \frac{1}{j\omega C}\,\dot{I} \notag \\
&= -j\frac{1}{\omega C}\,\dot{I} \tag{10}
\end{align}
$$
である。ここで$${-j}$$は、指数関数表示すると、
$$
e^{j-\frac{\pi}{2}} = \cos\left(-\frac{\pi}{2}\right)+j\sin\left(-\frac{\pi}{2}\right) = -j \tag{11}
$$
より、位相を$${90\degree}$$遅らせる働きを持っている。よって、式(10)より、コイルの電圧$${\dot{V}}$$は、電流$${\dot{I}}$$より$${90\degree}$$遅れるので、ベクトル図は、図7のようになる。
基本素子の組み合わせによるベクトル図
基本素子のベクトル図をもとに基本素子を組み合わる時のベクトル図を考える。
図8の回路において、ベクトル図を図示していく。

ベクトル図を書く際には、基準を決めることが必要である。今回は、$${\dot{I}}$$を基準にしてベクトル図を書いていく。最初に図9に示すように基準となるベクトルを書く。

次に、抵抗の電圧ベクトル$${\dot{V}_{\rm{R}}}$$を書いていく。式(7)で見たように抵抗の電圧と電流は同相であるから、図10のようになる。

次に、コイルの電圧ベクトル$${\dot{V}_{\rm{L}}}$$を書いていく。式(8)で見たようにコイルの電圧は電流に対して、$${90\degree}$$進みであるから、図11のようになる。

最後に電圧ベクトル$${\dot{V}}$$は、$${\dot{V}_{\rm{R}}}$$と$${\dot{V}_{\rm{L}}}$$の足し算であるから、図12のようになる。

このように基準ベクトルを決めて、各要素ごとにベクトルを追加していけば全体のベクトル図がかける。コンデンサが回路にあった場合でも、各要素ごとに書いていけば良い。ただし、コンデンサとコイルが両方ある場合は、その長さに注意する必要がある。どちらの方が大きいのかによって、ベクトルの長さを変えないといけない。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
