
同期発電機のベクトル図
同期発電機の等価回路
同期発電機の1相分の等価回路は、図1に示すような回路となる。

図1より、
$$
\dot{E} = \dot{V}+\left(R_{a}+jx_{s}\right)\dot{I}\tag{1}
$$
が成り立つことがわかる。
同期発電機のベクトル図
式(1)を端子電圧$${\dot{V}}$$を基準ベクトルとして、ベクトル図で表すと、図2のようになる。なお、端子電圧$${\dot{V}}$$と負荷電流$${\dot{I}}$$の位相差を$${\theta}$$としている。
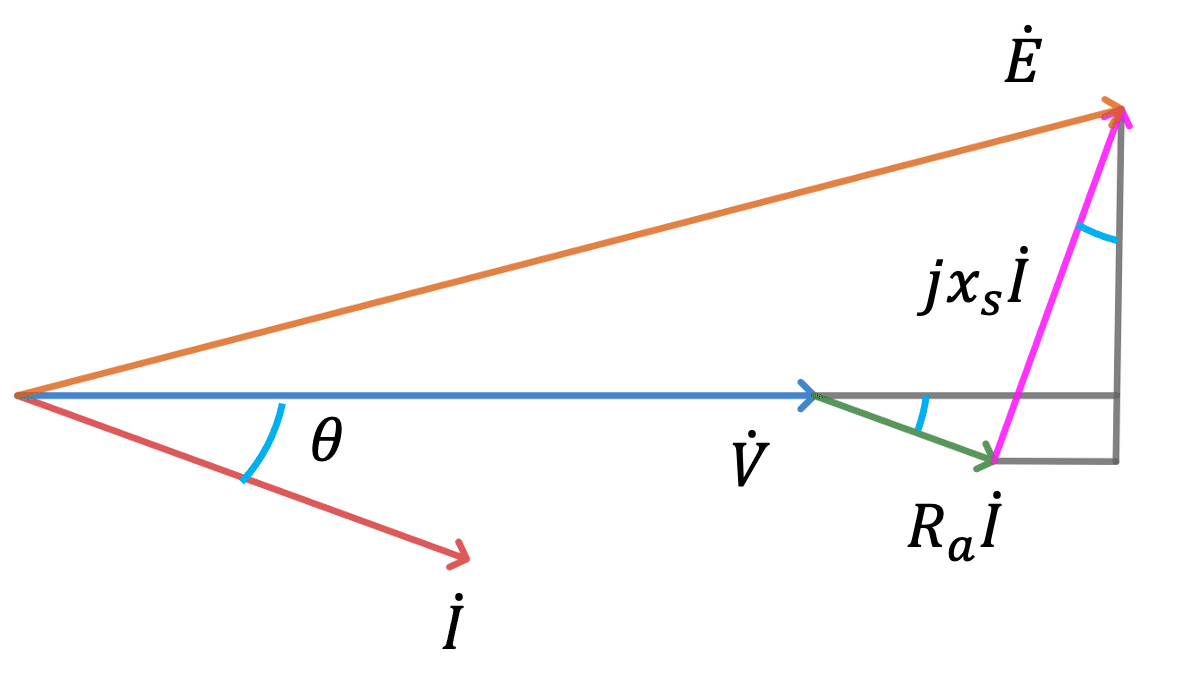
図2のベクトル図において、電機子抵抗$${R_{a}}$$で発生する電圧$${R_{a}\dot{I}}$$は、負荷電流$${\dot{I}}$$と同相なので、端子電圧$${\dot{V}}$$となす角度は、$${\theta}$$になる。
図2の右側に着目したものを図3に示す。

図3において、三角形abcと三角形efcに着目すると、$${\angle \rm{abc}}$$と$${\angle \rm{efc}}$$は、$${90\degree}$$である。$${\angle \rm{acb}}$$と$${\angle \rm{ecf}}$$は、対頂角なので等しい。よって、残った角度$${\angle \rm{bac}}$$と$${\angle \rm{fec}}$$は、等しくなり、その角度は$${\theta}$$である。
式(1)の内部誘導起電力$${\dot{E}}$$の大きさ$${E}$$は、図4に示す三角形で求めれる。

図4では、線分afと線分efの大きさが分かっていない。
そこで、図5からその大きさを求める。

図5から線分afは、線分agと線分gfを足せば良いことが分かる。
線分agは、負荷電流の大きさを$${I}$$とすれば、
$$
line_{ag} = R_{a}I\cos(\theta)\tag{2}
$$
で求まる。
線分gfは、線分bdと同じ長さなので、
$$
line_{gf} = x_{s}I\sin(\theta)\tag{3}
$$
となる。
よって、線分afは、
$$
line_{af} = line_{ag}+line_{gf} = R_{a}I\cos(\theta)+x_{s}I\sin(\theta)\tag{4}
$$
となる。
次に図5から、線分efは、線分edから線分fdを引けば求まることが分かる。
線分edは、
$$
line_{ed} = x_{s}I\cos(\theta)\tag{5}
$$
となる。
線分fdは、線分gbと同じ長さなので、
$$
line_{fd} = R_{a}I\sin(\theta)\tag{6}
$$
となる。
よって、線分efは、
$$
line_{ef}=line_{ed}-line_{fd}=x_{s}I\cos(\theta)-R_{a}I\sin(\theta)\tag{7}
$$
と求まる。
線分afと線分efがわかったので、端子電圧の大きさを$${V}$$とすれば、図4から、内部誘導起電力の大きさ$${E}$$は、
$$
E=\sqrt{\left(V+R_{a}I\cos(\theta)+x_{s}I\sin(\theta)\right)^{2}+\left(x_{s}I\cos(\theta)-R_{a}I\sin(\theta)\right)^{2}}\tag{8}
$$
となる。
なお、視覚的にイメージしやすいように式(8)を導出したが、式(1)において、負荷電流$${\dot{I}=I(\cos(\theta)-j\sin(\theta))}$$となることおよび、端子電圧を基準ベクトルとすることに気をつけると、
$$
\begin{align}
\dot{E} &= \dot{V}+\left(R_{a}+jx_{s}\right)\dot{I}\notag\\
&= V+\left(R_{a}+jx_{s}\right)I(\cos(\theta)-j\sin(\theta))\notag\\
&= V+R_{a}I\cos(\theta)+x_{s}I\sin(\theta)+j(x_{s}I\cos(\theta)-R_{a}I\sin(\theta))\notag\\
E &= \sqrt{\left(V+R_{a}I\cos(\theta)+x_{s}I\sin(\theta)\right)^{2}+\left(x_{s}I\cos(\theta)-R_{a}I\sin(\theta)\right)^{2}}\tag{9}
\end{align}
$$
と直接、式(1)から導出できる。
電機子抵抗を考慮しない場合は、$${R_{a}=0}$$となるので、
$$
E = \sqrt{\left(V+x_{s}I\sin(\theta)\right)^{2}+\left(x_{s}I\cos(\theta)\right)^{2}}\tag{10}
$$
となる。
関連記事の変圧器の電圧変動率でも同様の結果が得られるが、
これは、図6に示すように回路状況的に電圧2つの間に、抵抗とリアクタンスが入るという状況が同じためである。

電験2種や電験1種取得を目指している人向けに書くと、図7に示すような電力系統の計算でも同じ式が出てくる。

すなわち、電圧が2つあって、その間に抵抗やリアクタンスがある場合は、すべて式(1)や式(9)の式で、同じように考えることができる。
これで記憶することが少なくなった。
関連記事
変圧器の電圧変動率
https://note.com/elemag/n/n5dbd65775cbd?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
