
配電方式
配電方式
発電所で作られた電気は特別高圧で送電され、配電用変電所にて高圧($${6.6\,\rm{kV}}$$など)に変換される。一般に配電用変電所から各需要家(各家庭やビルなど)までの電力系統を配電系統という。配電系統において、低圧需要家に電気を送るには、高圧を低圧へと変換しなければならない。この変換する際の電線接続の仕方について見ていく。
また、単相と三相は理解している方を対象としている。
単相2線式
単相2線式は、図1に示すような配電方式である。

単相なので、線が2本あれば電力を送ることができる。
単相2線式の電力損失を考えていく。図2には、図1の2次側のみを示す。

電線の抵抗を$${R}$$、負荷の電力を$${P}$$、力率を$${\cos(\theta)}$$、電流を$${I}$$とする。
負荷の電力$${P}$$は、
$$
P=VI\cos(\theta)
$$
で求まる。
電線には、負荷の電流$${I}$$が流れる。電線は2本分あるので、線路損失$${P_{\rm{L}}}$$は、
$$
P_{\rm{L}} = 2RI^{2}
$$
と求まる。
単相3線式
単相3線式を図3に示す。

単相3線式は、変圧器の中性点を接地し、中性線を取り出した方式である。
これにより、図3に示すように大きさが異なる電圧を得ることができる。
単相3線式の電力損失を考える。図3の2次側を図4に示す。

各端子間が同じ大きさの電力を持っているとき、これを平衡状態という。図4では、単相負荷が、それぞれ$${P}$$である。
また、単相3線式の全体の合計電力$${P_{0}}$$は、
$$
P_{0} = 2P=2VI\cos(\theta)
$$
となる。
ここで、各負荷が平衡状態であるとき、図4の赤線で示した電流と青線で示した電流は大きさが同じで逆向きに流れるので、中性線には見かけ上、電流が流れない。
よって、単相3線式の線路損失$${P_{\rm{L}}}$$は、中性線以外の電線の抵抗を考えれば良いので、
$$
\begin{align}
&\notag\\
P_{\rm{L}} &= 2RI^{2}\notag\\
\end{align}
$$
となる。
注) 負荷が平衡状態でない場合は、中性線にも電流が流れるため、その場合は、中性線の抵抗も考える必要がある。
単相2線式と比較すると、線路損失が同じまま2倍の電力を送れるようになっている。
また、単相2線式で単相3線式と同じ電力を送るには、電流をより多く流す必要があるため、電線を太くする必要がある。これは通常、電力系統では電圧は一定に制御されるためである。
電流は、電力の式から、
$$
\begin{align}
2VI_{3}\cos(\theta)&=VI_{2}\cos(\theta)\notag\\
I_{2} = 2I_{3}\tag{1}
\end{align}
$$
となる。ここで、$${I_{2}}$$は、単相2線式の電流、$${I_{3}}$$は、単相3線式の電流を表す。
線路損失は、同じなので、
$$
\begin{align}
2R_{2}{I_{2}}^{2} &= 2R_{3}{I_{3}}^{2}\notag\\
\frac{R_{3}}{R_{2}}&=\frac{{I_{2}}^{2}}{{I_{3}}^{2} }\notag\\
&=\left(\frac{2I_{3}}{I_{3}}\right)^{2}=4\tag{2}
\end{align}
$$
となる。途中で式(1)の関係を使用した。
電線の抵抗$${R}$$は、断面積$${A}$$、抵抗率$${\rho}$$、長さ$${l}$$とすると、
$$
R=\rho\frac{l}{A}
$$
で求まる。今、電線の長さ$${l}$$および、抵抗率$${\rho}$$は同じとして、単相2線式の抵抗$${R_{2}}$$と単相3線式の抵抗$${R_{3}}$$の比を考えると、
$$
\begin{align}
\frac{R_{3}}{R_{2}} &= \frac{\rho\frac{l}{A_{3}}}{\rho\frac{l}{A_{2}}}\notag\\
&= \frac{A_{2}}{A_{3}}\notag\\
\end{align}
$$
となる。式(2)の関係から、
$$
\begin{align}
\frac{R_{3}}{R_{2}} &= \frac{A_{2}}{A_{3}}=4\tag{3}\\
\end{align}
$$
と求まる。
電線の単位体積あたりの質量を$${\sigma}$$、体積を$${V}$$とすれば、電線の質量$${W}$$は、
$$
W = \sigma V
$$
で求まる。
体積$${V}$$は、図5に示すように断面積$${A}$$と長さ$${l}$$をかければ良い。

よって、電線の質量$${W}$$は、
$$
W = \sigma Al
$$
となる。
単相2線式の電線の質量$${W_{2}}$$と単相3線式の電線の質量$${W_{3}}$$の比は、
$$
\begin{align}
\frac{W_{3}}{W_{2}}&= \frac{3\sigma A_{3}l}{2\sigma A_{2}l}\notag\\
&= \frac{3}{2}\frac{A_{3}}{A_{2}}\tag{4}\\
\end{align}
$$
となる。単相2線式は、電線が2本なので2倍、単相3線式は3本なので3倍する必要がある。
ここに、式(3)の関係を使うと、
$$
\begin{align}
\frac{W_{3}}{W_{2}}&= \frac{3}{2}\frac{A_{3}}{A_{2}}=\frac{3}{2}\frac{1}{4} = \frac{3}{8}= 0.375\notag\\
\end{align}
$$
となる。なお、単相3線式の中性線の断面積も他の線と同じ断面積としている。
よって、単相2線式と単相3線式が同じ電力を送るとき、単相3線式は、単相2線式の$${37.5\%}$$の電線質量で送れるということになる。つまり、$${62.5\%}$$電線量が節約できている。
三相3線式
三相3線式を図6に示す。

三相3線式は、図6に示すように単相変圧器3台をΔ結線する方法や、Y結線する方法、三相変圧器を使用する方法がある。
三相3線式が送電できる電力$${P_{3}}$$は、Δ結線やY結線によらず、
$$
P_{3} = \sqrt{3}VI\cos(\theta)
$$
となる。
関連記事を参照してほしい。
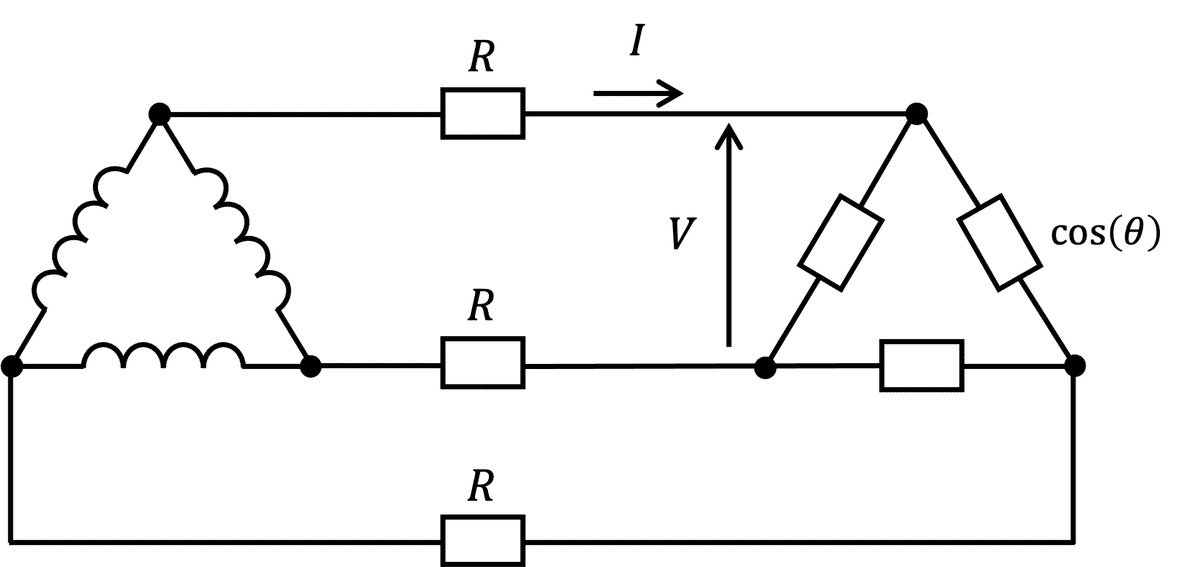
三相3線式の線路損失を考える。図7に図6の2次側を示す。
電線の抵抗$${R}$$を流れる電流は$${I}$$なので、線路損失$${P_{\rm{L}}}$$は、
$$
\begin{align}
&\notag\\
P_{\rm{L}} &= 3RI^{2}\notag\\
\end{align}
$$
となる。
単相2線式と比較していく。
単相2線式の電線質量を$${W_{2}}$$、三相3線式の電線質量を$${W_{3}}$$とすると、式(4)より、
$$
\begin{align}
\frac{W_{3}}{W_{2}}&= \frac{3\sigma A_{3}l}{2\sigma A_{2}l}\notag\\
&= \frac{3}{2}\frac{A_{3}}{A_{2}}\notag\\
\end{align}
$$
となる。
断面積の比を求めるために、電流の比を求める。
電力の式
$$
\begin{align}
\sqrt{3}VI_{3}\cos(\theta)&=VI_{2}\cos(\theta)\notag\\
I_{2} = \sqrt{3}I_{3}\notag
\end{align}
$$
線路損失の式
$$
\begin{align}
2R_{2}{I_{2}}^{2} &= 3R_{3}{I_{3}}^{2}\notag\\
\frac{R_{3}}{R_{2}}&=\frac{2}{3}\frac{{I_{2}}^{2}}{{I_{3}}^{2} }\notag\\
&=\frac{2}{3}\left(\frac{\sqrt{3}I_{3}}{I_{3}}\right)^{2}=2\notag
\end{align}
$$
式(3)から
$$
\begin{align}
\frac{R_{3}}{R_{2}} &= \frac{A_{2}}{A_{3}}=2\notag\\
\end{align}
$$
よって、電線質量の比は、
$$
\begin{align}
\frac{W_{3}}{W_{2}}&= \frac{3\sigma A_{3}l}{2\sigma A_{2}l}\notag\\
&= \frac{3}{2}\frac{A_{3}}{A_{2}}\notag\\
&= \frac{3}{2}\frac{1}{2} = 0.75\notag
\end{align}
$$
となる。
したがって、単相2線式が三相3線式と同じ電力を送る場合、三相3線式は単相2線式の$${75\%}$$の電線質量で送ることができる。つまり、$${25\%}$$の質量を削減できる。
三相4線式
三相4線式を図8に示す。

三相4線式は、中性点を接地し、中性線を取り出すことで、単相電力も取り出せるようにした方式である。
単相3線式と三相3線式を組み合わせたような方式と考えるとわかりやすい。
三相4線式は、図9に示すように、V結線を用いることもある。
単相電力は、電灯負荷などに使用し、三相電力は、電動機などの負荷に使用する。

三相4線式の線路損失を考える。図10に図8の2次側を示す。

この状態では、単相と三相が混在しているので、1相分の回路で考える。図11に1相分の回路を示す。

三相4線式の場合、中性線があるが、単相3線式と同様に負荷が平衡状態であれば、中性線には見かけ上、電流が流れないため、中性線の抵抗を考える必要がない。
線路損失は三相3線式の時と同様に、
$$
P_{\rm{L}} = 3RI^{2}
$$
となる。
図11から電力を求める。
単相電力$${P_{1}}$$
$$
P_{1} = V_{1}I_{1}\cos(\theta)
$$
三相電力$${P_{3}}$$
$$
P_{3} = \frac{V_{3}}{\sqrt{3}}I_{3}\cos(\theta)
$$
ここで、$${\frac{V_{3}}{\sqrt{3}}=V_{1}}$$なので、
$$
P_{3} = \frac{V_{3}}{\sqrt{3}}I_{3}\cos(\theta)=V_{1}I_{3}\cos(\theta)
$$
よって、合計電力は3つ分を考慮して、
$$
\begin{align}
P &= 3(P_{1}+P_{3})\notag\\
&=3(V_{1}I_{1}\cos(\theta)+V_{1}I_{3}\cos(\theta))\notag\\
&=3V_{1}(I_{1}+I_{3})\cos(\theta)\notag\\
\end{align}
$$
となる。また、図11より$${I = I_{1}+I_{3}}$$であり、$${V_{1}}$$を単相2線式と同様に$${V}$$で表すと、
$$
\begin{align}
P &= 3V_{1}(I_{1}+I_{3})\cos(\theta)\notag\\
&= 3VI\cos(\theta)\notag\\
\end{align}
$$
となる。
単相2線式の電線質量を$${W_{2}}$$、三相4線式の電線質量を$${W_{4}}$$とすると、三相4線式は電線が4本なので、
$$
\begin{align}
\frac{W_{4}}{W_{2}}&= \frac{4\sigma A_{4}l}{2\sigma A_{2}l}\notag\\
&= 2\frac{A_{4}}{A_{2}}\notag\\
\end{align}
$$
となる。
断面積の比を求めるために、電流の比を求める。
電力の式
$$
\begin{align}
3VI_{4}\cos(\theta) &=VI_{2}\cos(\theta)\notag\\
I_{2} = 3I_{4}\notag\\
\end{align}
$$
線路損失の式
$$
\begin{align}
2R_{2}{I_{2}}^{2} &= 3R_{4}{I_{4}}^{2}\notag\\
\frac{R_{4}}{R_{2}}&=\frac{2}{3}\frac{{I_{2}}^{2}}{{I_{4}}^{2} }\notag\\
&=\frac{2}{3}\left(\frac{3I_{4}}{I_{4}}\right)^{2}=6 \notag
\end{align}
$$
式(3)から
$$
\begin{align}
\frac{R_{4}}{R_{2}} &= \frac{A_{2}}{A_{4}}=6\notag\\
\end{align}
$$
よって、電線質量の比は、
$$
\begin{align}
\frac{W_{4}}{W_{2}}&= \frac{4\sigma A_{4}l}{2\sigma A_{2}l}\notag\\
&= \frac{4}{2}\frac{A_{4}}{A_{2}}\notag\\
&= \frac{4}{2}\frac{1}{6} = 0.333\notag
\end{align}
$$
となる。
したがって、単相2線式が三相4線式と同じ電力を送る場合、三相4線式は単相2線式の$${33.3\%}$$の電線質量で送ることができる。つまり、$${66.7\%}$$の質量を削減できる。
なおここで示した、電線質量の計算はあくまで1例であるため、負荷の状況や接続の仕方によっては、成り立たないこともある。
特に、負荷が不平衡の場合はそれぞれの条件を考慮して計算する必要がある。
関連記事
直流と交流の電力
https://note.com/elemag/n/n8243e21d941f?sub_rt=share_pw
Δ結線
https://note.com/elemag/n/nbd92bde1cdcd?sub_rt=share_pw
Y結線
https://note.com/elemag/n/n69982181d762?sub_rt=share_pw
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
