
令和元年度 理論科目 問16 電験3種過去問
問題
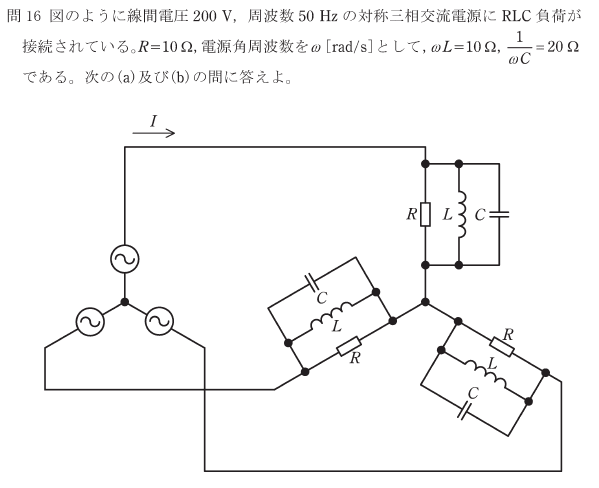

考え方
(a)は、1相分の回路で考える。
(b)は、1相分の有効電力を3倍して3相分にする。
解答例
(a)
1相分の回路は図1に示すようになる。

図1の合成インピーダンス$${\dot{Z}}$$は、
$$
\begin{align}
\dot{Z} &= \frac{1}{\frac{1}{10}+\frac{1}{j10}+\frac{1}{-j20}} \notag\\
&= \frac{1}{0.1-j0.1+j0.05}\notag\\
&= \frac{1}{0.1-j0.05}\notag\\
&= \frac{1}{0.0125}(0.1+j0.05)\notag\\
&= 8+j4 \, Ω\tag{1}
\end{align}
$$
となる。電源電流$${\dot{I}}$$は、
$$
\begin{align}
&\notag\\
\dot{I} &= \frac{\frac{200}{\sqrt{3}}}{8+j4}\notag\\
&= \frac{200}{\sqrt{3}\times 80}(8-j4)\notag\\
&= 11.54 - j 5.77 \,\rm{A}\tag{2}
\end{align}
$$
と求まる。電源電流$${\dot{I}}$$の大きさ$${I}$$は、
$$
I = \sqrt{11.54^{2} + 5.77^{2}} = 12.9\, \rm{A}\tag{3}
$$
となる。よって、(a)の答えは(3)である。
(b)
式(2)より図1の回路の電力は、
$$
\begin{align}
&\notag\\
P+jQ &= \frac{200}{\sqrt{3}}\overline{(11.54 - j 5.77)}\notag\\
&= \frac{200}{\sqrt{3}}(11.54 + j 5.77)\notag\\
&= 1332.5 + j666.3\, \rm{V\cdot A}\tag{4}
\end{align}
$$
と求まる。よって、三相負荷の有効電力は、式(4)の実部を3倍すれば良いので、$${1332.5\times 3 = 3.99 \, \rm{kW}}$$と求まる。
したがって、(b)の答えは(4)である。
サイト
https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0
