変圧器の等価回路

理想変圧器

実際の変圧器をいきなり考えるのは難しいので、まずは理想的な変圧器において、どのような関係が成り立つのかをみていく。理想的な変圧器は図1に示すように、巻線の抵抗が無視でき、一次側コイルで発生する磁束が、全て二次巻線を通過する変圧器である。また、鉄心で生じる鉄損などの損失も全て無視する。

図1 理想変圧器

理想変圧器の一次側端子に正弦波電圧$${\dot{V}_{1}}$$を与えると、一次巻線では、一次電流$${\dot{I}_{1}}$$が流れ、図2のように一次巻線に磁束$${\Phi}$$が発生する。磁束$${\Phi}$$の向きは、右ねじの法則から、上向きになる。

図2 理想変圧器の一次側

一次巻線に磁束$${\Phi}$$が発生すると、一次巻線では磁束の変化による起電力が生じる。起電力の向きは、レンツの法則から電流の変化を妨げる向きに発生する。したがって、図3のような起電力$${\dot{E}_{1}}$$が発生する。これにより、下向きの磁束ができる。

図3 一次巻線に発生する電圧

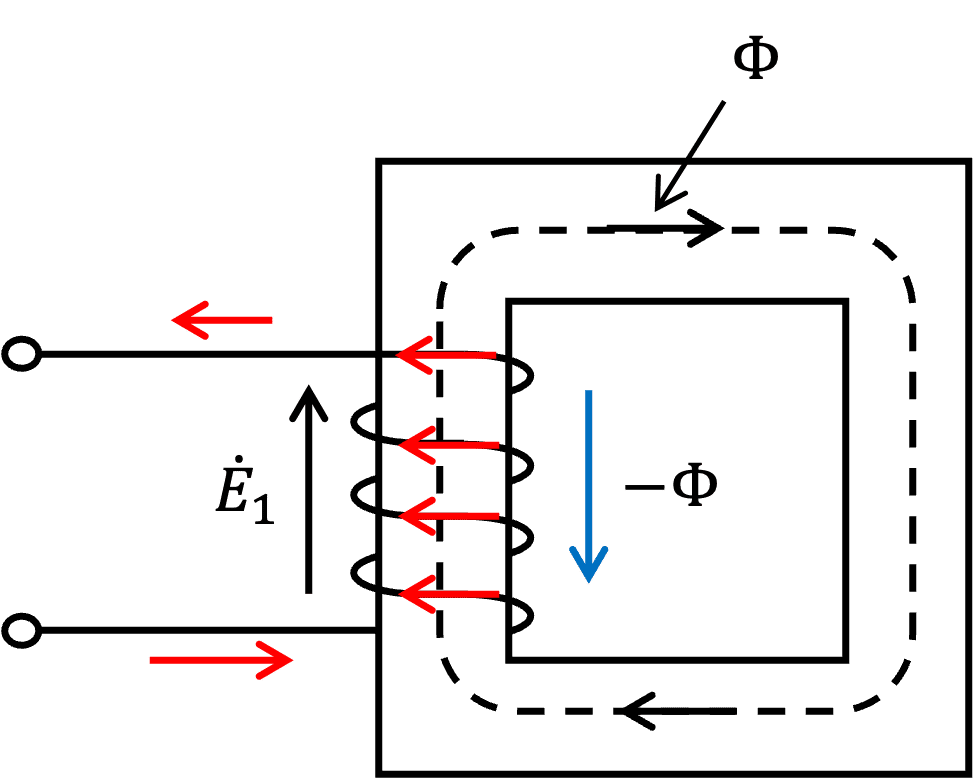
一次巻線の起電力のイメージは、図4のような回路を考えることと同じである。
すなわち一次巻線から、一次側に電流を供給するような状態になる。
基本的に、変化をなくそうとするので、図4のような起電力が発生すれば、一次電流$${\dot{I}_{1}}$$を弱めることになり、変化を無くそうと作用することが分かる。

図4 一次巻線の起電力のイメージ

次に二次巻線側を考える。図5に示すように磁束$${\Phi}$$を打ち消す方向に磁束を作ろうとすると、電流は、図5に示すような流れとなる。二次巻線の起電力の向きは、一次巻線の時と同様に考えると、二次巻線から、二次側に電流を供給するような状態になる。したがって、起電力の向きは、上向きになる。二次巻線の起電力のイメージは、図6のような回路を考えることと同じである。

図5 二次巻線に発生する電圧

図6 二次巻線の起電力のイメージ

よって、図1に示すような起電力の向きになる。
次に図1に示す理想変圧器において、図7の回路図で無負荷時を考える。

図7 理想変圧器の無負荷時

ファラデーの電磁誘導の法則より、巻線に発生する起電力の大きさは、

$$
E=-N\frac{{\rm{d}}\Phi}{{\rm{d}}t}\tag{1}
$$

であるから、一次巻線と二次巻線の電圧は、

$$
\begin{align}
E_{1}&=-N_{1}\frac{{\rm{d}}\Phi}{{\rm{d}}t}\tag{2}\\
E_{2}&=-N_{2}\frac{{\rm{d}}\Phi}{{\rm{d}}t}\tag{3}\\
\end{align}
$$

となる。
一次側端子に正弦波電圧を与えているため、磁束も正弦波になるとすると、
磁束$${\Phi}$$は、最大値を$${\Phi_{m}}$$として、

$$
\Phi=\Phi_{m}\sin(\omega t)\tag{4}
$$

となることから、式(4)を式(2)および式(3)に代入すると、

$$
\begin{align}
E_{1}&=-N_{1}\frac{{\rm{d}}\Phi}{{\rm{d}}t}\notag\\
&= -N_{1}\frac{{\rm{d}}\Phi_{m}\sin(\omega t)}{{\rm{d}}t}\notag\\
&= -\omega N_{1} \Phi_{m}\cos(\omega t)\notag\\
&= \omega N_{1} \Phi_{m}\sin\left(\omega t-\frac{\pi}{2}\right)\tag{5}\\
E_{2}&=-N_{2}\frac{{\rm{d}}\Phi}{{\rm{d}}t}\notag\\
&= -N_{2}\frac{{\rm{d}}\Phi_{m}\sin(\omega t)}{{\rm{d}}t}\notag\\
&= -\omega N_{2} \Phi_{m}\cos(\omega t)\notag\\
&= \omega N_{2} \Phi_{m}\sin\left(\omega t-\frac{\pi}{2}\right)\tag{6}\\
\end{align}
$$

となる。
式(5)および式(6)より、実効値は、

$$
\begin{align}
E_{1}&= \frac{1}{\sqrt{2}}\omega N_{1} \Phi_{m}\notag\\
&= \frac{1}{\sqrt{2}}2\pi f N_{1} \Phi_{m}\notag\\
&= 4.44 f N_{1} \Phi_{m}\tag{7}\\
E_{2}&= \frac{1}{\sqrt{2}}\omega N_{2} \Phi_{m}\notag\\
&= \frac{1}{\sqrt{2}}2\pi f N_{2} \Phi_{m}\notag\\
&= 4.44 f N_{2} \Phi_{m}\tag{8}\\
\end{align}
$$

となる。
一次巻線と二次巻線の電圧の比を取ると、

$$
\frac{E_{1}}{E_{2}}=\frac{4.44 f N_{1} \Phi_{m}}{4.44 f N_{2} \Phi_{m}}=\frac{N_{1}}{N_{2}}\tag{9}
$$

となる。$${\frac{N_{1}}{N_{2}}}$$を巻数比といい$${a}$$で表す。
次に図8に示すように負荷がある場合を考える。

図8 理想変圧器の負荷時

二次電流$${\dot{I}_{2}}$$が流れるため、図9に示したような磁束が発生する。

図9 二次電流による磁束

そのため、一次巻線では、図10に示すように、一次電流がこの磁束を打ち消すためにさらに流れることになる。

図10 二次電流による磁束が発生した時の一次側

この時、どのくらいの一次電流が流れるかを見ていく。
図9で二次電流$${\dot{I}_{2}}$$によって、作られる磁束$${\Phi}$$は、磁気回路の考え方をすると、鉄心の磁気抵抗を$${R_{l}}$$として、

$$
\Phi=\frac{N_{2}I_{2}}{R_{l}}\tag{10}
$$

となる。よって、二次電流$${\dot{I}_{2}}$$によって、作られる磁束$${\Phi}$$を打ち消すには、一次電流による起磁力と、二次電流による起磁力が等しくないといけないので、

$$
N_{1}I_{1}=N_{2}I_{2}\tag{11}
$$

となる。巻数比で考えると式(11)を変形して、

$$
\frac{N_{1}}{N_{2}}=\frac{I_{2}}{I_{1}}\tag{12}
$$

となる。
よって、巻数比$${a}$$は、次の関係がある。

$$
a=\frac{N_{1}}{N_{2}}=\frac{E_{1}}{E_{2}}=\frac{I_{2}}{I_{1}}\tag{13}
$$

変圧器の等価回路

ここからは、理想変圧器をもとにして、実際の変圧器を考えていく。
実際の変圧器では、巻線に抵抗がある。図示すると図11のようになる。

図11 巻線の抵抗を追加

次に図1では、一次巻線で発生した磁束が、全て二次巻線を通過するように考えたが、実際には、図12に示すように二次巻線を通過しない磁束もある。同様に二次巻線で発生する磁束も、全てが一次巻線を通過することはない。これを漏れ磁束という。漏れ磁束は、それぞれの巻線のみにしか作用しないため、それぞれの巻線の自己インダクタンスの成分を、主磁束を作るための自己インダクタンスと漏れの自己インダクタンスに分けることができる。

図12 漏れ磁束のイメージ

よって、各巻線には漏れインピーダンスがある。図11は、図13のようになる。

図13 漏れインピーダンスを追加

最後に、磁束を作るための励磁回路を見ていく。
鉄心の中を磁束が通る際、鉄心では、ヒステリシスや渦電流による損失が生じる。これを鉄損という。これにより、励磁回路は鉄損を生じる抵抗成分と、磁束を作るインダクタンス成分とに分けて考えることができる。また、二次側が開放状態でも、図2で見たように、一次側には、電流が流れる。したがって、図13の一次巻線と並列に接続する必要がある。よって、図14のような等価回路が成り立つ。
磁気回路のインピーダンスは、通常、アドミタンスとして表す。これは、インピーダンスとして表すと、値が大きくなるためである。

図14 現実的な等価回路

T型等価回路

図14では、理想変圧器の部分が残っているため、これを取り除くことを考える。
理想変圧器の部分では、式(13)の巻数比を考えることができるため、二次側の値を一次側に換算することができる。二次電流$${\dot{I}_{2}}$$、二次巻線抵抗$${r_{2}}$$、二次漏れインピーダンス$${x_{2}}$$、二次端子電圧$${\dot{V}_{2}}$$は式(13)より、一次側に換算すると、

$$
\begin{align}
\dot{I_{1}}^{\prime} &= \frac{\dot{I}_{2}}{a}\tag{14}\\
\dot{V_{2}}^{\prime} &= a\dot{V}_{2}\tag{15}\\
{r_{2}}^{\prime} &= a^{2}r_{2}\tag{16}\\
{x_{2}}^{\prime} &= a^{2}x_{2}\tag{17}\\
\end{align}
$$

となる。式(16)と式(17)においては、

$$
\begin{align}
r^{\prime} &= \frac{V_{1}}{I_{1}}\notag\\
&= \frac{aV_{2}}{\frac{I_{2}}{a}}\notag\\
&= a^{2}r_{2}\tag{18}
\end{align}
$$

となることを用いている。
よって、理想変圧器を取り除いて、一次側に換算した等価回路は図15のようになる。これをT型等価回路という。

図15 T型等価回路

L型等価回路

T型等価回路では、励磁回路が間に入っているため、計算を行う際に複雑になってしまう。そこで、励磁回路を電源側に移動した等価回路を考える。
励磁回路を電源側に移動すると、図16に示すような等価回路になる。これをL型等価回路という。

図16 L型等価回路

このようなことができるのは、一次側のインピーダンス降下が一次電圧に比べて、十分に小さいこと、かつ励磁電流が一次電流に比べて十分小さいことが成立する場合である。幸いにも現実的には、L型等価回路で計算を行っても、十分な精度を保てることがほとんどである。そのため、通常はL型等価回路が使用される。
しかし、精密に変圧器を取り扱う必要がある場合は、T型等価回路を用いる必要がある。

サイト

https://sites.google.com/view/elemagscience/%E3%83%9B%E3%83%BC%E3%83%A0