お題：カットケーキを3等分せよ！計算した後で調査したら数学選手権で凄いのが出てきた

糖質カット75%のチーズケーキを買ってみた。高いものではないけれども、家族分買って失敗したくない。前回あまり同じ店で買った商品の評価がよくなったので。

それで、自分で味見しようと思って１つだけ買ったものの、やはり評価を聞こうかと。3等分しよう。

お題：カットケーキを３等分せよ！

全体３６０度の３０度分もないカットケーキ。１０度ずつ切るのも難しいし、細すぎて倒れたのを食べるのは味気ない。

いい方法はないものか！そうだ、三角に小さく切って、残りを2等分すれば簡単に切れそうだ。

しかし、どの当たりで切ればいいものか。。。計算してみた。

ホールケーキの中心から半径をｒとして、面積計算。30度（１／１２）として、半径のどれだけの比率にすればいいかを計算してみた。

まぁ、計算してみて当たり前だが、半径も角度も関係ない。

　1/√3　≒　0.577　

倍の長さで扇形にくり抜けばよい。よし、どうだ！

一つ大きいぞ？錯覚か？

うーむ、明らかに三角が多く見える。錯覚じゃないかな？色が違うだけで同じ円の大きさも違って見えるからね。

検証だ！

じゃ、ちゃんと図で書いて比べてみる。

やっぱり三角が大きく見える。

自分の計算を信じて家族に勧める。理系の娘が、「重さ量ってみれば？」

確かに。２ｇしか違わない。切り取り線の内側・外側ぐらいの違いだろう。誤差の範囲だ。計算は間違ってなさそう。めでたしめでたし。

数学好きが考える3等分が凄い！

さて、これだけでは終わらない。せっかくなので3等分の仕方を調べてみた。カットケーキは出てこなかったが、円の３等分で凄いのが出てきた。ホールケーキと思えばいい。

「数学を愛する会」なる会で選手権をしたらしい。その名も「円を3等分する方法選手権」！

まずは入賞作品です。もともとは円なので、ケーキとかイメージした切り方になってません。

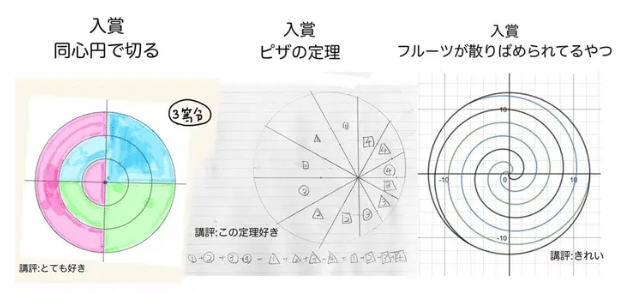
ケーキに載っているトッピング場所によってはメチャメチャ差がでそう。

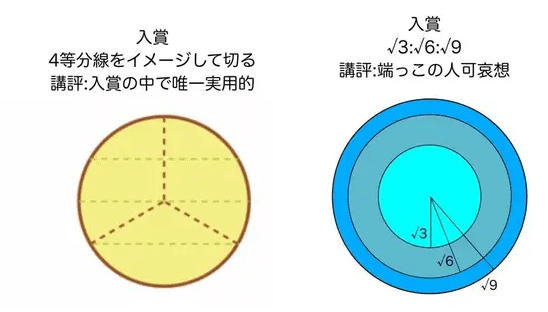
次は入賞した中で実用的な３等分。左は受験数学で３０度の場合の比率を思い出しますね。

そして、最優秀賞がこちら。

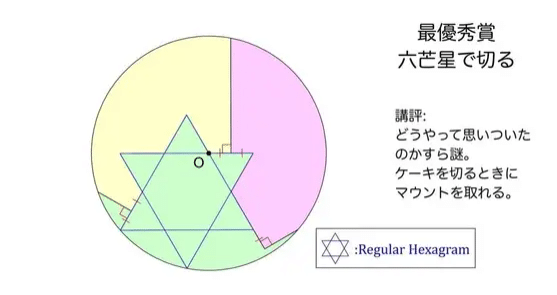
「六芒星」が出るかぁ。どういう比率でどこから切ればいいんだ～？

いずれにせよ、ケーキ３等分から始まって、六芒星まで、楽しませていただきました。

えっ？ケーキの味はどうだったかって？

75％糖質カットを考慮すれば、軽めのチーズケーキだけどおいしゅうございました！