
エスカレーター、どっちに立つ?
皆さんはエスカレーターに乗るとき、右側と左側どっち側に立ちますか?
東京では左側に立って右側を歩きますよね。大阪ではその逆で、右側に立って左側を歩く。
他方で仙台では先に立った人の数で決まるようです。右側に立っている人が多ければ右に、左側に立っている人が多ければ左に立つという具合です。
このエスカレーターの右側と左側どちらに立つかという現象はどのように決まるのでしょうか。
今回はそれを進化ゲーム理論の力を借りて説明していきます。
進化ゲーム理論とは
進化ゲーム理論は、ゲーム理論の概念や手法を生物の進化に適用した理論です。ゲーム理論は、複数の意思決定者(プレイヤー)が互いに影響を及ぼし合う状況を分析する理論です。
進化ゲーム理論とゲーム理論の違いは、先読みの有無です。ゲーム理論では、プレイヤーは自分の行動の結果を他のプレイヤーの行動などと照らし合わせて予測し、自分にとって最も都合のよさそうな戦略を取ると仮定します。一方、進化ゲーム理論では先読みを仮定せず、実際にある戦略を取った後に、それがうまくいったかどうかによって戦略のシェアが増減する、という仮定をおきます。
進化ゲーム理論の最大の特徴であり、画期的な点は、人々の相互作用によって変化する戦略の割合とそれがどう変化するか、つまり「ダイナミクス」を捉えられることです。
進化ゲーム理論の開発の過程で、集団中の戦略頻度の時間変化を微分方程式で表す方法が考案されました。これは「レプリケーター・ダイナミクス」と呼ばれています。また、レプリケーター・ダイナミクスの結果として、ある一つの戦略が集団中に生き残ることがありますが、この戦略は「進化的に安定な戦略(Evolutionarily Stable Strategy,ESS)」と呼ばれます。
進化ゲーム理論の設定
では、エスカレーターの右側と左側どちらに立つかという現象を進化ゲーム理論のモデルで考えていきます。
大量の人がいたるところで 2 人ゲームを行うことを想定します。
2つの戦略:右に立つ or 左に立つ
効用:同じ側に立ったときのみ1の利得が生じる (別の側に立つと互いに邪魔になるので)
ちなみにこのように「他人と同じ行動を選ぶことがよい」とされるゲームは「調整ゲーム」「協調ゲーム」と呼ばれます。
各人の利得は以下の利得表のようになると仮定します。

時刻 𝑡の右に立つ人の割合: 𝑥(𝑡)
割合なので 0≤𝑥(𝑡)≤1
「右側に立つ」の利得:期待利得
𝑢(右)=𝑥(𝑡)×1+(1−𝑥(𝑡))×0=𝑥(𝑡)
「左側に立つ」の利得:期待利得
𝑢(左)=𝑥(𝑡)×0+(1−𝑥(𝑡))×1=1−𝑥(𝑡)
全体の平均利得:期待利得
𝑢=𝑥(𝑡)𝑢(右)+(1−𝑥(𝑡))𝑢(左)
=𝑥(𝑡)^2+(1−𝑥(𝑡))^2
「右」の利得−全体の平均利得
=𝑢(右)−𝑢
=𝑥(𝑡)−𝑥(𝑡)^2−(1−𝑥(𝑡))^2
=(1−𝑥(𝑡))(2𝑥(𝑡)−1)
時刻の変化をどうとらえるか?
わずかな時間: Δ𝑡
わずかな時間の間の割合の変化: Δ𝑥(𝑡)
Δ𝑥(𝑡)=𝑥(𝑡+Δ𝑡)−𝑥(𝑡)
戦略の割合について以下の法則が成立します。
法則1:戦略の割合は、その戦略が全体の平均より多くなったら増える
全体の平均より少なくなったら減る
法則2:割合の変化は、その戦略が得る利得に比例する
この法則に従うと、わずかな時間の間の割合の変化、すなわち、Δ𝑥(𝑡)を以下のように記述できます。
わずかな時間の間の割合の変化=(「右」の利得−全体の平均利得)(時刻 𝑡の右に立つ人の割合)(わずかな時間)
Δ𝑥(𝑡)=(u(右)-u) 𝑥(𝑡)Δ𝑡
例えば、ここで(「右」の利得−全体の平均利得)が1、(時刻 𝑡の右に立つ人の割合)が0.7、(わずかな時間)を0.01(秒)として考えます。
すると、0.01秒の間に1×0.7×0.01=0.007 だけ「右側に立つ」戦略の割合が増えることになります。
つまり、0.01秒後の「右側に立つ」戦略の割合は 0.7×(1+0.007)=0.7049 となります。
基本的に、
「右」の利得−全体の平均利得 >0
である限り、
「右側に立つ」戦略の割合は増える
逆に、
「右」の利得−全体の平均利得 <0
である限り、
「右側に立つ」戦略の割合は減る
Δ𝑥(𝑡)=(u(右)-u) 𝑥(𝑡)Δ𝑡
を変形すると、
Δ𝑥(𝑡)/Δ𝑡=(u(右)-u) 𝑥(𝑡)
となります。
Δ𝑡を限りなく0に近づけた場合にこの式が微分方程式になることに注目します。
Δ𝑡を限りなく0に近づけた場合にΔ𝑥/Δ𝑡が限りなく近づく値が𝑑𝑥(𝑡)/𝑑𝑡です。
つまり、Δ𝑥(𝑡)/Δ𝑡=(u(右)-u) 𝑥(𝑡) は
微分方程式として以下のように表すことができます。
𝑑𝑥(𝑡)/𝑑𝑡=(u(右)-u)𝑥(𝑡)
(u(右)-u)=(1−𝑥(𝑡))(2𝑥(𝑡)−1) でしたから
𝑑𝑥(𝑡)/𝑑𝑡= (1−𝑥(𝑡))(2𝑥(𝑡)−1)𝑥(𝑡) ー(1)
となります。
このように戦略頻度の時間変化を微分方程式で表す方法を「レプリケーター・ダイナミクス」と呼びます。
微分は「傾き」、すなわち、ある瞬間における増加率を求める行為ですから、
次の瞬間、戦略の割合は(1)式の右辺に従って増減することになります。
(1)式の右辺は3次関数であり、グラフで表すと以下のようになります。

このグラフを見ると、ある瞬間において戦略の割合がどう変化するか、つまり、ダイナミクスがわかります。
曲線が𝑥軸と交わる点、すなわち、y=0 となる点は定常点と呼ばれ、ダイナミクスが動かない点です。今回では、(0, 0)、(0.5, 0)、(1, 0) の三つの点が定常点です。
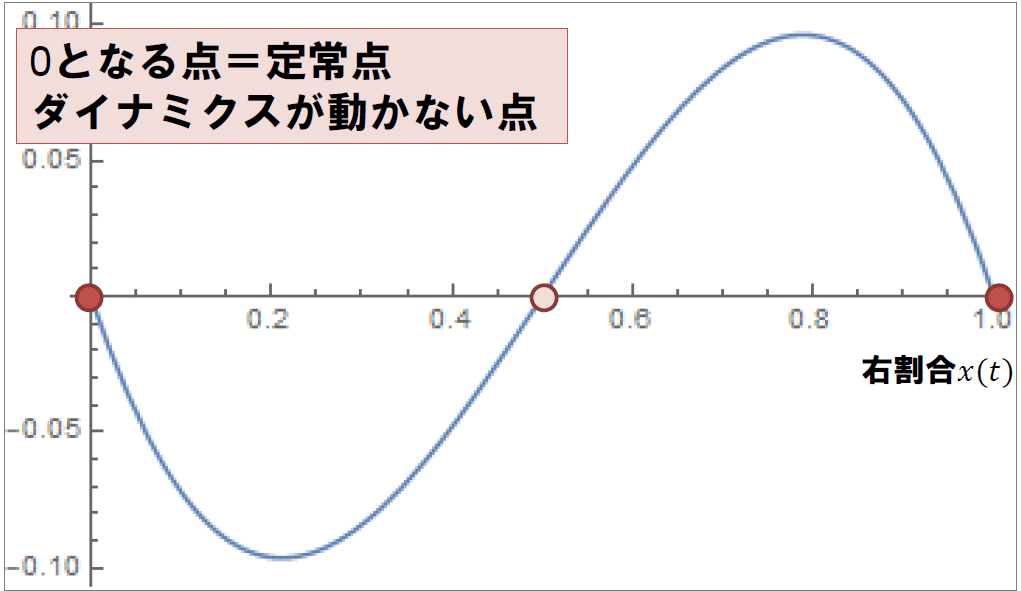
曲線が𝑥軸より上にある時、右側に立つ戦略の割合、すなわち、𝑥(𝑡)は増加します。
逆に曲線が𝑥軸より下にある時、𝑥(𝑡)は減少します。

レプリケーター・ダイナミクスの結果として、ある一つの戦略が集団中に生き残ることがあり、それをESS(進化的に安定な戦略)と呼ぶと述べました。今回取り上げた事象では、ESSは二つあり、進化的に安定的な状態が二つあります。全員が右側に立つ戦略を選ぶ状態(𝑥(𝑡)=1)と全員が左側に立つ戦略を選ぶ状態(𝑥(𝑡)=0)です。この二つの状態はとても安定的な状態です。たとえ𝑥の値が少し変化したとしても、元の位置に戻る力が働きます。𝑥=0.5 の時も定常点ですが、この点から少しでも右にずれると、戦略の割合は増加し続け、最終的に𝑥=1の点で止まります。左にずれた場合は、戦略の割合は減少し続け、最終的に𝑥=0の点で止まります。進化的に安定的な点と不安定な定常点の違いは少しずれても元に戻るか、少しずれると元に戻らないというところにあります。

以上の分析結果をまとめると、
𝑥=0:全員左(東京式)
𝑥=1:全員右(大阪式)
このどちらかが実現していることになります。
また、不安定な状態が一つありました。
𝑥=0.5:右と左が半々
この状態だと少しでもバランスが崩れるとそちらに集中し、やがて全員右か全員左になります。
つまり、仙台で、もし右側に立つ人と左側に立つ人の割合が半々になる場合があったとしても、やがて全員右か全員左の状態になることを意味します。
また、全員右になるか全員左になるかは𝑥(𝑡)の初期値の違いとして説明できるでしょう。
𝑥(0)の位置が 0.5 よりも大きいか小さいかによって𝑥(𝑡)の値が1と0のどちらに帰結するかが決まります。
今回はモデルと現実の乖離が少なく、上手く事象を説明することができたようです。
