品質管理検定 #26-08-001
[問8]
抜き取り検査に関する次の文章において、$${\boxed{\space}}$$内に入るもっとも適切なものを下欄のそれぞれの選択肢からひとつ選びなさい。ただし、各選択肢を複数回用いることはない。なお、回答にあたって必要であれば付表を用いよ。
① 次の条件でJIS Z 9002-1956 計数規準型一回抜取検査を考える。
なるべく合格させたいロットの不適合品率の上限 $${p_0=0.6\%}$$
なるべく不合格にしたいロットの不適合品率の下限 $${p_1=6.5\%}$$
生産者危険 $${{\alpha\fallingdotseq}{\space}0.05}$$
消費者危険 $${{\beta\fallingdotseq}{\space}0.10}$$
抜取方法は、サンプルの大きさ $${n=\boxed{(45)}}$$、合格判定個数 $${c=\boxed{(46)}}$$ となる。また、図8.1においてこのときのOC曲線は$${\boxed{(47)}}$$ である。

② 図8.1において合格判定個数を変えずにサンプルの大きさを増加させると、OC曲線は$${\boxed{(48)}}$$。また、サンプルの大きさを変えずに合格判定個数を増加させると、OC曲線は$${\boxed{(49)}}$$。
$${\boxed{(45)}{\space}\boxed{(46)}}$$の選択肢
ア . 0 イ. 1 ウ. 2 エ. 3 オ. 4
カ. 30 キ. 40 ク. 60 ケ. 80 コ. 100
$${\boxed{(47)}}$$の選択肢
ア. a イ. b ウ. c
$${\boxed{(48)}\space\boxed{(49)}}$$の選択肢
ア. $${\Iota}$$に近づく イ. $${\Iota\Iota}$$に近づく ウ. 変わらない
正解
(45) ク. 60
(46) イ. 1
(47) イ. b
(48) ア. $${\Iota}$$に近づく
(49) イ. $${\Iota\Iota}$$に近づく
製品の合否はロット単位で考えます。「ロット」とは、品質が同等と考えることが出来る塊です。もちろん、ロット内でもある程度のばらつきがあり、単体で見れば適合品も不適合品もあります。そのロットから一部をサンプルとして検査をして全体で合格か不合格かを決めます。
問題文から
なるべく合格させたいロットの不適合品率の上限 $${p_0=0.6\%}$$
なるべく不合格にしたいロットの不適合品率の下限 $${p_1=6.5\%}$$
生産者危険 $${{\alpha\fallingdotseq}{\space}0.05}$$
消費者危険 $${{\beta\fallingdotseq}{\space}0.10}$$
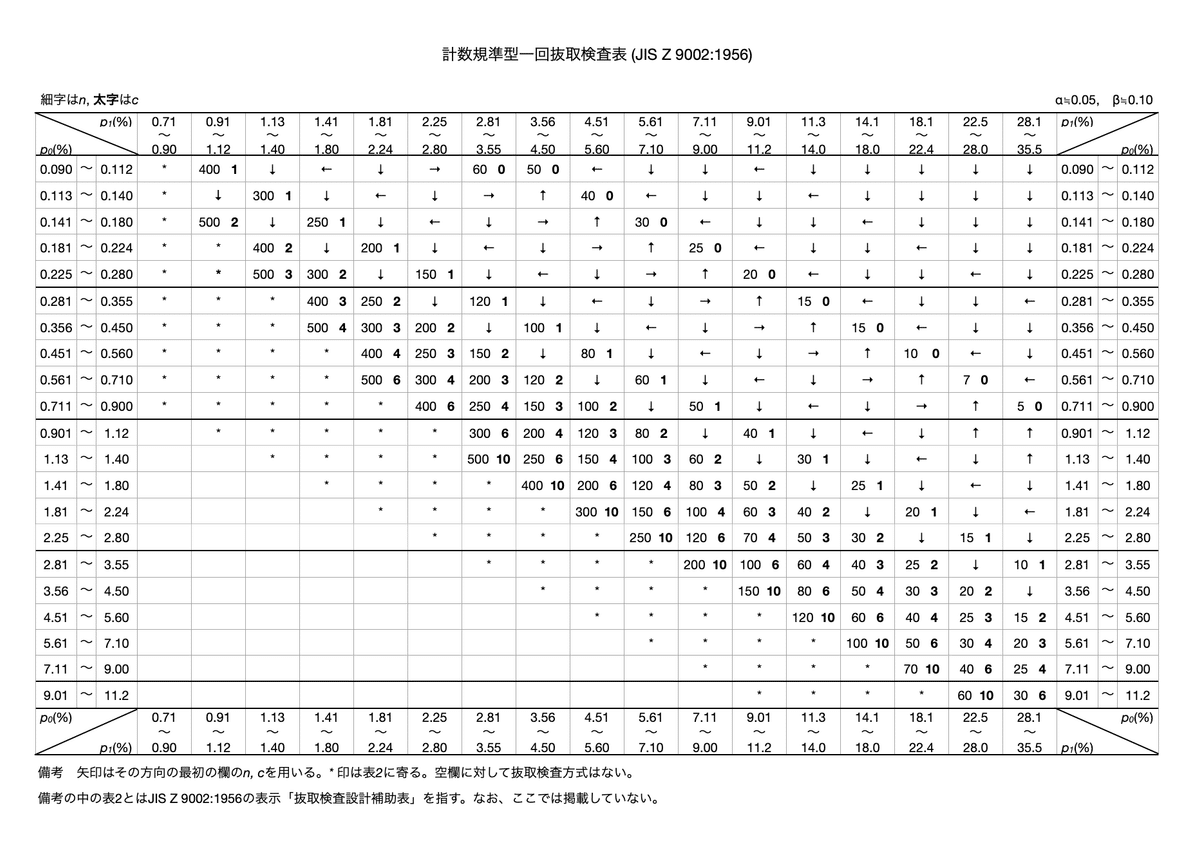
これをもとに計数規準型一回抜取検査表を調べます。付表は、$${{\alpha\fallingdotseq}{\space}0.05}$$、$${{\beta\fallingdotseq}{\space}0.10}$$のものしかありません。右上に書いてありますので、念のため確認します。
$${p_0=0.6\%}$$ と $${p_1=6.5\%}$$ の交点の数字です。矢印の場合は、数字になるまで矢印の方向に進みます。
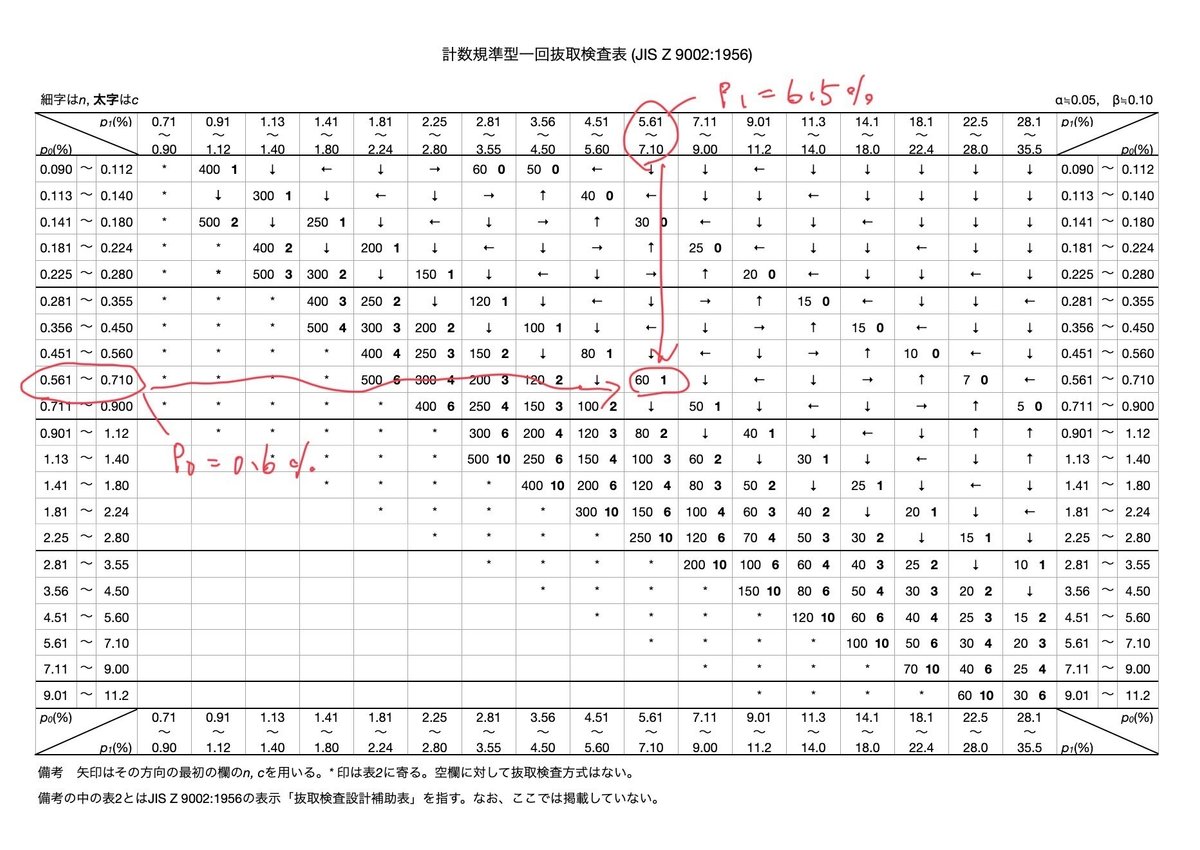
n=60(サンプル数), c=1(合格判定個数<何個の不良までなら合格にするか>)が分かります。(45) (46)
現実の検査員で、「厳しい分には良い」と考えて、勝手にサンプル数を増やす人がいます。これは品質過剰でコスト上昇につながったり、生産が出来なくなったりしますので、検査員の教育、指導は理由を説明して、正しく行うように理解してもらわなければなりません。
OC曲線問題。Operating Characteristic Curveといいます。

生産した製品は全数を検査しないことがほとんどです。一部を検査して、ロット全体の合否を決定します。そのため、サンプルも適合品を拾うか、不適合品を拾うかのばらつきが生じます。
横軸は「ロットの不適合品率」、縦軸は「ロットの合格する確率」です。「不適合品率」が高い(右側ほど不適合品率が高い)ほど、「ロットの合格率」は下がります。全体に不適合品が多いほど、サンプルにも不適合品は多くなるからです。
なるべく合格させたいロットの不適合品率の上限 $${p_0=0.6\%}$$
があります。それでも全数検査じゃないですから、不適合品率が0.6%以下でもロットが不合格になる可能性はあります。これが生産者危険で、ここでは$${{\alpha}{\fallingdotseq\space}0.5}$$ですね。曲線の上側が不合格範囲です。縦軸の一番上が合格確率1なので、そこから0.5下がって、右に進んだOC曲線との交点がロットの不適合品率0.6%(横軸)になります。細かいので、問題の解答としては判断しにくいです。
なるべく不合格にしたいロットの不適合品率の下限 $${p_1=6.5\%}$$
があります。こちらも不適合品率が6.5%以上でも合格になってしまう可能性があります。消費者に不良品が回ってくる可能性が高まるので、それを消費者危険$${\beta{\fallingdotseq\space}0.10}$$ としています。
曲線の下側が合格範囲なので、縦軸の0から0.1上勝手、右に進んだOC曲線との交点が6.5%になります。そのOC曲線は「b」ですね。(47)
生産者危険$${\alpha}$$を「あわて者の危険($${{\alpha}watemono}$$」、消費者危険を「ぼんやり者の危険($${{\beta}onyarimono}$$」とかいいますが、そんな言い方をしてもどっちがどっちか分かるとも思えません😅 単にアルファベットの順番で、($${\alpha}$$)生産してから、($${\beta}$$)消費者へ、と考えたほうが良いと思います。
合格判定個数を変えないでサンプル数を増やした場合、検査の数が増えるので、不適合品を見つける可能性も増えます。つまり不合格になりやすくなります。縦軸はロットの合格する確率ですから、OC曲線は下がります。OC曲線よりも下側が合格、OC曲線よりも上側が不合格なので、下側(合格側)の面積が減って、上側(不合格側)の面積が増えます。OC曲線は$${\Iota}$$ に近づきます。(48)
サンプルの大きさを変えずに合格判定個数を増加させると、不適合品が多く検出されても合格判定個数内である可能性が高くなりますから、ロットの合格する確率は上がります。OC曲線の下側(合格側)の面積が増えて、OC曲線の上側(不合格側)の面積が減りますから、OC曲線は$${\Iota\Iota}$$ に近づきます。(49)
この問題は解きかただけじゃなく、一回は抜取検査表とOC曲線の意味を理解しておけば正答できると思います。何となく、の理解ではちょっと怪しいです。また、実務においても生産数から検査数と合格判定個数を正しく決めることができます。意味も分からずに過去の他製品の実績から検査数や合格判定個数を決めることは、事情が異なる場合もありますからやめたほうが良いです。数字の根拠を訊かれても、「前と同じにしました」じゃ、前の設定は大丈夫なの?と訊かれたらお終いです🥲 試験に合格することはメリットがありますが、正しく運用できることはとても意義があり、あなたへの信頼度は上がるでしょうし、その所属全体でのメリットにもなります。
ではー。
