時系列分析入門【第１章】Rデータセットの時系列データをPythonでプロットする

2023年10月30日 19:45

この記事は、テキスト「RとStanではじめる心理学のための時系列分析入門」の第１章「心理学と時系列データ分析」のRスクリプトをお借りして、Pythonで「実験的」に実装する様子を描いた統計ドキュメンタリーです。

取り扱いテーマは、時系列データのグラフ描画です。
時系列データの特徴をビジュアルで楽しみましょう！

テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。

テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。

第１章心理学と時系列データ分析

インポート

この章で用いるライブラリをインポートします。

### インポート

# 基本
import numpy as np
import pandas as pd

# Rデータセット・一般化線形モデル・時系列分析
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.tsa.seasonal import seasonal_decompose

# wavファイル操作
import soundfile

# WEBアクセス
import requests

# グラフ描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')

【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。

### インストール

## statsmodels
# anaconda
conda install -c conda-forge statsmodels
# pip
pip install statsmodels

## soundfile
# pip
pip install soundfile

## requests
# anaconda
conda install -c anaconda requests
# pip
pip install requests

1.2.1 時系列データの条件

R言語の標準データセットから２つの時系列データを取得して、時系列推移をグラフに描画します。

■ R標準データセットをPythonで利用
「statsmodels」ライブラリの「get_rdataset」関数を用いて、R の標準データセットを取得します。
次のリンクはRdatasetsサイトです。
このサイトで「Package」と「Item」の２項目を確認して、データ利用します。

① ナイル川の流量データ（Nileデータ）
Rデータセットを読み込みます。

### データセットの読み込み
# 第１引数：Item, 第２引数：Package
data_nile = sm.datasets.get_rdataset('Nile', 'datasets')

データセットの説明を見てみましょう。

### データセットの説明
print(data_nile.__doc__)

【実行結果】
データセットの簡単な説明書きを確認できました。

データを見てみましょう。
「.data」でpandasのデータフレームに格納されたNileデータを表示できます。

### データセットの表示
data_nile.data

【実行結果】
time列に「年」、value列に「流量」がセットされています。
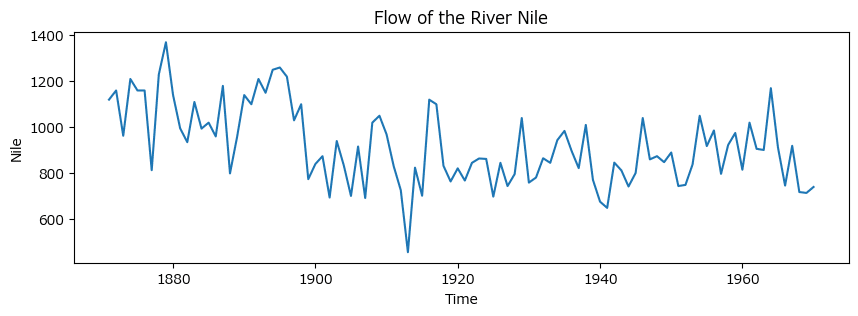
1871年～1970年にエジプト・アスワンで計測されたナイル川の流量です。

図1.2(a)のナイル川の流量のグラフを描画します。

### 時系列グラフの描画
plt.figure(figsize=(10, 3))
plt.plot(data_nile.data.time, data_nile.data.value)
plt.title(data_nile.title)
plt.xlabel('Time')
plt.ylabel('Nile');

【実行結果】

② 販売時系列データ（BJsalesデータ）
Rデータセットを読み込みます。

### データセットの読み込み
data_bjsales = sm.datasets.get_rdataset('BJsales', 'datasets')

データを見てみましょう。

### データセットの表示
data_bjsales.data

【実行結果】
time列に「時系列番号」、value列に「売上高」がセットされています。
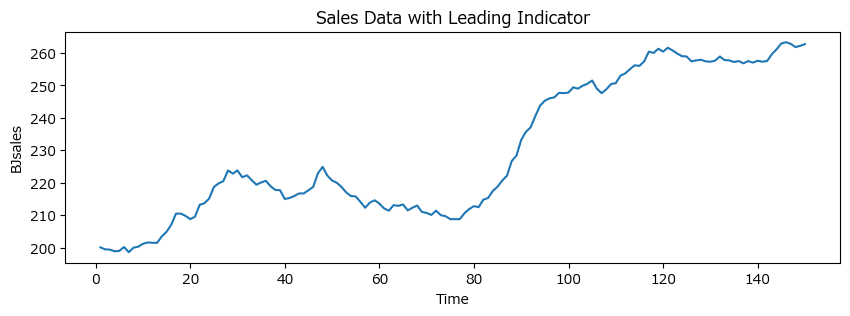
150か月の売上データです。

図1.2(b)の販売データのグラフを描画します。

### 時系列グラフの描画
plt.figure(figsize=(10, 3))
plt.plot(data_bjsales.data.time, data_bjsales.data.value)
plt.title(data_bjsales.title)
plt.xlabel('Time')
plt.ylabel('BJsales');

【実行結果】

1.4.1 時系列データの分解

この節にRコードはありませんが、時系列データを成分分解するイメージがあると、以後のコードの理解が進むのでは？と考えてテキストの図1.6の計算式を引用いたします。

時系列の観測値＝レベル成分＋トレンド成分＋季節成分＋外因性成分＋誤差

テキスト11ページの図1.6の内容を改変して引用

1.4.2 レベル成分とトレンド成分

レベル成分は切片、トレンド成分は傾きに相当します。
レベル・トレンド成分を取り出してグラフ描画します。

$${CO_2}$$濃度のRデータセットを読み込みます。

### データセットの読み込み
data_co2 = sm.datasets.get_rdataset('co2', 'datasets')

データを見てみましょう。

### データセットの表示
data_co2.data

【実行結果】
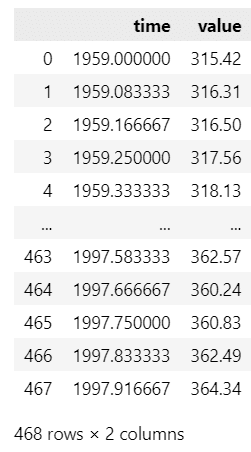
time列に「年月」、value列に「濃度」がセットされています。
1959年1月～1997年12月の$${CO_2}$$濃度データのようですが、月が小数（月/12）になっています。

レベル・トレンド成分を取得しましょう。
statsmodelsのseasonal_decomposeを用いて、トレンド変動（レベルを含む）・季節変動・不規則変動に分離して、result_co2に格納します。
12か月周期を仮定して、period=12を指定します。

### トレンド成分・季節成分・不規則変動成分に分離
result_co2 = seasonal_decompose(data_co2.data.value, model='additive',
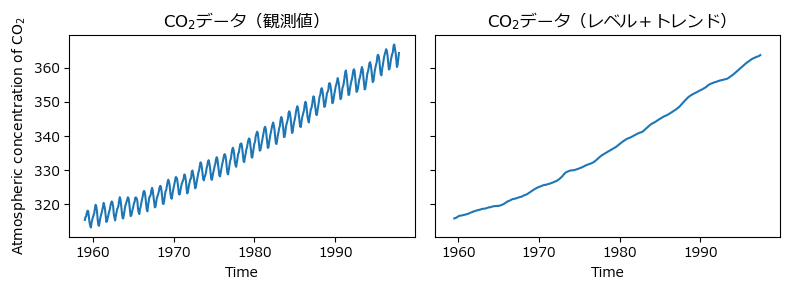
                                period=12, two_sided=True)

図1.7の２つのグラフを描画しましょう。
レベル＋トレンド成分は「result_co2.trend」で取得できます。

### 時系列グラフの描画
fig, ax = plt.subplots(1, 2, figsize=(8, 3), sharex=True, sharey=True)
# 観測値を描画
ax[0].plot(data_co2.data.time, data_co2.data.value)
ax[0].set_title('$CO_2$データ（観測値）')
ax[0].set_xlabel('Time')
ax[0].set_ylabel('Atmospheric concentration of $CO_2$')
# トレンド成分を描画
ax[1].plot(data_co2.data.time, result_co2.trend)
ax[1].set_title('$CO_2$データ（レベル＋トレンド）')
ax[1].set_xlabel('Time')
plt.tight_layout();

【実行結果】
滑らかな右肩上がりのトレンドを確認できました。

result_co2に格納した「トレンド成分」・「季節成分」・「不規則変動成分」を描画しましょう。
１行で描けます！

### おまけ：トレンド成分・季節成分・不規則変動成分のプロット
result_co2.plot();

【実行結果】

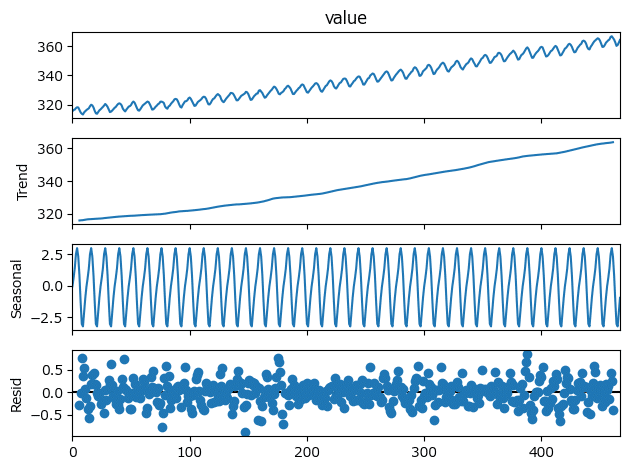
1.4.3 季節成分

季節成分は周期的に繰り返す成分です。
季節成分を取り出してグラフ描画します。

太陽黒点のRデータセットを読み込みます。

### データセットの読み込み
data_sunspot = sm.datasets.get_rdataset('sunspot.year', 'datasets')

データを見てみましょう。

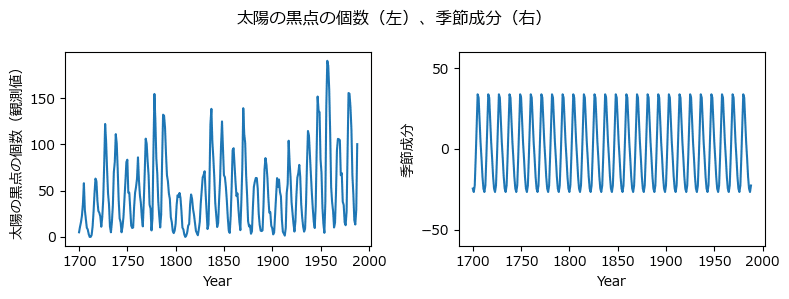
### データセットの表示
data_sunspot.data

【実行結果】
time列に「年」、value列に「黒点の個数」がセットされています。
1700年～1988年の太陽黒点の個数データです。

季節成分を取得しましょう。
11年周期を仮定して、period=11を指定します。

### トレンド成分・季節成分・不規則変動成分に分離
result_sunspot = seasonal_decompose(data_sunspot.data.value, model='additive',
                                    period=11, two_sided=True)

図1.8の２つのグラフを描画しましょう。
季節成分は「result_sunspot.seasonal」で取得できます。

### 時系列グラフの描画
fig, ax = plt.subplots(1, 2, figsize=(8, 3), sharex=True)
# 観測値を描画
ax[0].plot(data_sunspot.data.time, data_sunspot.data.value)
ax[0].set_xlabel('Year')
ax[0].set_ylabel('太陽の黒点の個数（観測値）')
# 季節成分を描画
ax[1].plot(data_sunspot.data.time, result_sunspot.seasonal)
ax[1].set_xlabel('Year')
ax[1].set_ylabel('季節成分')
ax[1].set_ylim(-60, 60)
ax[1].set_yticks([-50, 0, 50])
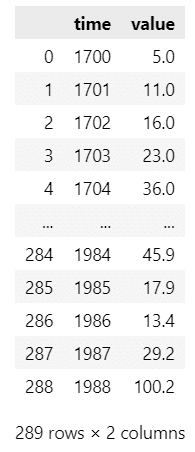
fig.suptitle('太陽の黒点の個数（左）、季節成分（右）')
plt.tight_layout();

【実行結果】
右側のグラフできれいな11年周期を確認できました。

result_sunspotに格納した「トレンド成分」・「季節成分」・「不規則変動成分」を描画しましょう。

### おまけ：トレンド成分・季節成分・不規則変動成分のプロット
result_sunspot.plot();

【実行結果】

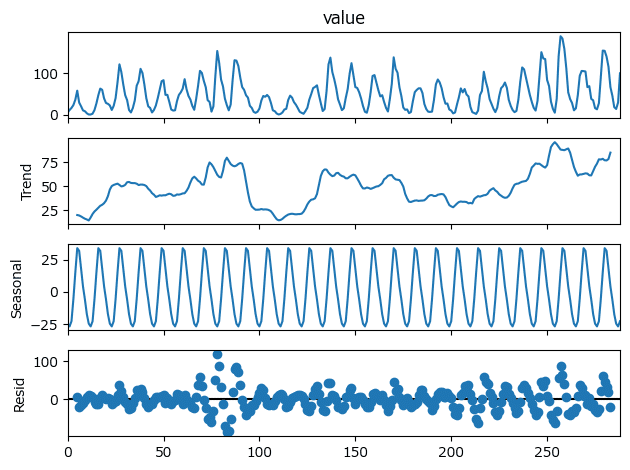
1.4.4 外因性成分

外因性成分は「介入」などの外部からの影響による変化です。
説明変数（exog）だと思います。
線形回帰分析を行い、切片と傾きを取得して、グラフ描画します。

では、図1.9を目指しましょう！
Nileデータは「1.2.1 時系列データの条件」で読み込み済みです。

アスワンハイダムの完成が1902年です。
ダムという外因によって、目的変数の流量が変化しています。
1902年前後での流量変化の赤い線を算出します。
statsmodelsのformula API を用いて一般化線形モデル（GLM）を構築します。
質的説明変数 x には、流量変化前の年＝0、流量変化後の年＝1を設定します。

### 流量変化（赤線）の取得
# x:流量変化前の年0, 流量変化後の年1を設定
x = [0] * (1902-1871+1) + [1] * (1970 - 1902)
# y:流量を設定
y = data_nile.data.value
# x, yをデータフレームに格納
data = pd.DataFrame({'y': y, 'x': x})
# GLMで流量変化線を算出
model = smf.glm(formula='y ~ x', data=data, family=sm.families.Gaussian()).fit()

GLMの分析結果を表示します。

### GLMの分析概要
print(model.summary())

【実行結果】
下段の「Intercept」約$${1060}$$は切片であり、流量変化前の流量を示します。
xの回帰係数（coef：傾き）約$${-207}$$は流量変化後の変化分であり、流量変化後の流量は「Intercept + xのcoef」で計算できます。

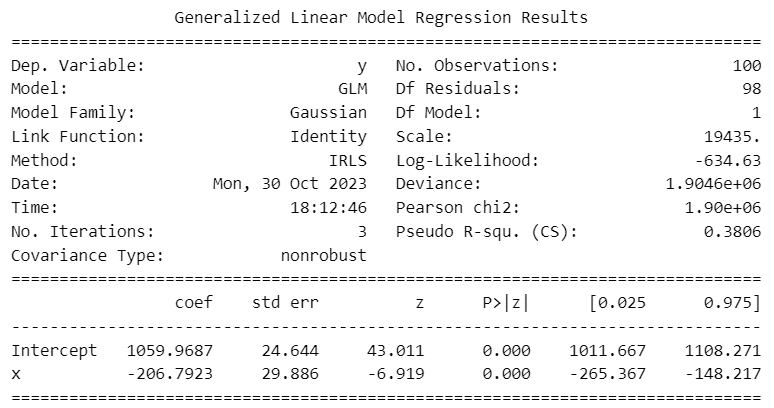
図1.9のグラフを描画しましょう。

### 時系列グラフの描画

plt.figure(figsize=(8, 4))
# 流量の観測値の描画
plt.plot(data_nile.data.time, data_nile.data.value)
# 流量変化の推定値の描画
plt.plot(data_nile.data.time, model.fittedvalues, color='red')
# 修飾
plt.title(data_nile.title)
plt.xlabel('Time')
plt.ylabel('Flow')
plt.ylim(0, 1550)
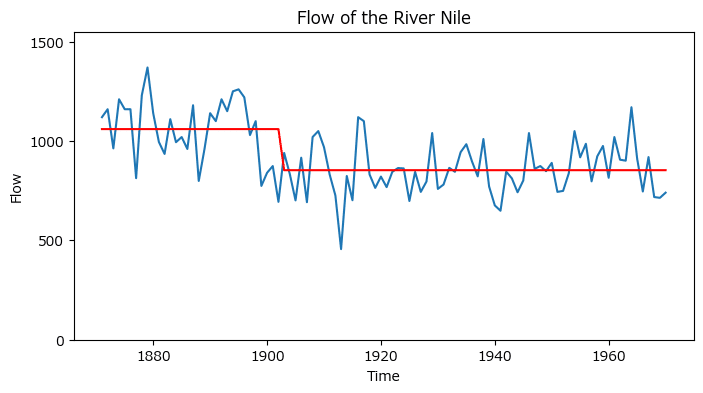
plt.yticks([0, 500, 1000, 1500]);

【実行結果】
statsmodelsで求めた流量変化を示す赤い線が入りました。

1.4.5 どの成分に興味を持つのか

図1.10の音声波形のグラフ描画に取り組みます。
まず、Webサイトから音声データ（wavファイル）をダウンロードしましょう。
「#設定」のfilenameにて、保存するファイルをパス付きで指定します。
コード例では作業フォルダにファイル名「bdl.wav」でダウンロードします。

### 音声データのダウンロード

# 設定：ダウンロードファイルの格納先パス＋ファイル名
filename = r'./bdl.wav'

# ダウンロードの実行
url = 'https://raw.githubusercontent.com/komorimasashi/time_series_book/' \
      '937bb1e53a8747a3d9b0838a50ee053e341b77ac/data/bdl.wav'
res = requests.get(url)
with open(filename, mode='wb') as f:
  f.write(res.content)

続いて、wavファイルに格納された波形を描画します。
soundfileを用います。
波形の値は$${-1~1}$$に正規化されており、テキストの値とは異なっています。

### wavファイルの波形データを描画 ※波形データは-1～1に正規化されている

# waveファイルを読み込んで、波形データとサンプリングレートfsを取得
sound_data, fs = soundfile.read(filename)

# 描画
plt.figure(figsize=(10, 4))
plt.plot(np.arange(len(sound_data)) / fs, sound_data, lw=0.3)
plt.xlabel('time')
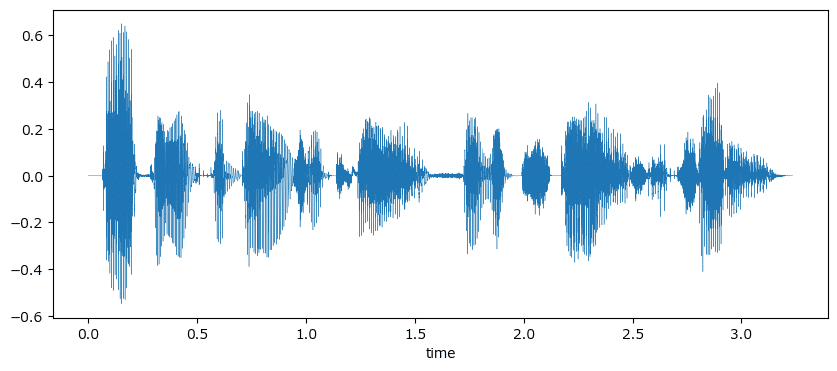
plt.show()

【実行結果】
簡単に描画できました！

【補足】
音声ファイルを扱う場合、librosaパッケージを用いることが多いです。
ただ、なぜだか自環境でlibrosaがうまく動かなかったので、代替案のsoundfileを用いました。
librosaのサンプルコードを置いておきます。

import librosa
y, sr = librosa.load(filename)
librosa.display.waveplot(y, sr=sr);

第２章へ続く

■次回の取り組みテーマ
ラグ、階差、移動平均、移動相関

次の記事

ブログの紹介

note で４つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．実験！たのしいベイズモデリングをPyMC Ver.5で

書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。

４．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

最後までお読みいただきまして、ありがとうございました。

時系列分析入門【第１章】Rデータセットの時系列データをPythonでプロットする

第１章 心理学と時系列データ分析

インポート

1.2.1 時系列データの条件

1.4.1 時系列データの分解

1.4.2 レベル成分とトレンド成分

1.4.3 季節成分

1.4.4 外因性成分

1.4.5 どの成分に興味を持つのか

第２章へ続く

ブログの紹介

いいなと思ったら応援しよう！

第１章心理学と時系列データ分析