
6-7 Xの二乗の期待値 ~ 分散の公式の本気度をEXCEL・Pythonで計算して確かめる
今回の統計トピック
分散の公式$${V[X]=E[X^2]-E[X]^2}$$をフル活用します。
実データを使って分散の公式を検証(実験)します!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
標本分布の分野
問7 $${X^2}$$の期待値(データなし)
試験実施年月
調査中(類似問題:統計検定2級 2016年11月 問11(回答番号21)
問題
公式問題集をご参照ください。
解き方
題意
平均と分散を手がかりにして、確率変数の二乗の期待値を計算します。
平均$${\mu}$$、分散$${\sigma^2}$$の分布に従う確率変数$${X}$$について、$${X^2}$$の期待値を求めます。
分散の公式
この問題は分散の公式に問題文の各値を当てはめて、答えを導きます。
分散$${V[X]=E[X^2]-E[X]^2}$$
($${Xの分散=X^2の期待値-Xの期待値^2}$$)
解きます
①分散の公式を整理します。
⇒$${E[X^2]=V[X]+E[X]^2}$$
②問題文から得られる確率変数$${X}$$の分散と平均を①の式に当てはめます。
・期待値$${E[X]}$$は確率変数$${X}$$の平均です。
・確率変数$${X}$$は平均$${\mu}$$、分散$${\sigma^2}$$の分布に従います。
つまり、確率変数$${X}$$の平均$${E[X]=\mu}$$、分散$${V[X]=\sigma^2}$$です。
⇒$${E[X^2]=\sigma^2+\mu^2}$$
答えは、$${X^2}$$の期待値$${E[X^2]=\sigma^2+\mu^2}$$です。
まとめ
今回の問題で「$${X}$$の分散+$${X}$$の平均の二乗は、$${X^2}$$の平均と等しい」ことが数式を展開して示されました。
え?数式を展開しただけでは等しさが伝わってこないですって?
解答
③ $${\mu^2+\sigma^2}$$ です。
難易度 やさしい
・知識:分散の公式
・計算力:数式組み立て(低)、数式計算(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、公式問題集で提示された「$${\boldsymbol{X}}$$の平均の二乗+$${\boldsymbol{X}}$$の分散は、$${\boldsymbol{X^2}}$$の平均と等しい」ことの正しさを実験して確かめます!
実験方法
実験の概念を図にしました。

Pythonでシミュレーションします
Pythonのコードを追いかけて、実験の臨場感を高めていきましょう!
①インポート
計算の得意な「NumPy」(ナンパイ)と、統計を頑張る「SciPy.stats」(サイパイ・スタッツ)の出番です。
「matplotlib.pyplot」(マットプロットリブ・パイプロット)はグラフ描画のスペシャリスト!
import numpy as np
from scipy.stats import norm
import matplotlib.pyplot as plt②確率変数$${X}$$データの生成
平均5、標準偏差100の正規分布$${N(5, 100^2)}$$の乱数を100個作成します。
# Xデータの生成(正規分布)
np.random.seed(1)
X = norm.rvs(5, 100, size=100)
# Xデータ概要の表示
print('Xのデータ型', type(X), ', 形状', X.shape)
print('Xの要素1~3番目の値', X[:3])【正規分布の乱数生成の解説】
norm.rvs(5, 100, size=100) を解体します。
・norm.rvs:正規分布の乱数を生成します。
・ 5 :平均です。
・100:標準偏差です。
・size=100:データ100個作ります。
【出力イメージ】
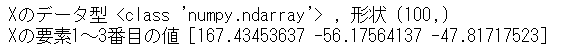
変数 X はNumPyの配列(ndarray)です。
NumPyの配列は柔軟に演算ができるので、使い勝手が良いです。
変数 X の二乗もしやすいのです!
形状 100 は、配列の中に100個のデータが入っていることを示しています。
③確率変数$${X}$$から$${X^2}$$データの生成
X2 = X**2 の1行で、Xの中の100個のデータ全てを二乗して、変数 X2 に代入しています。
X2が$${X^2}$$データです。
# XデータからX^2データを作成
X2 = X**2 # Numpy配列Xの全ての要素を二乗してX2に代入
# X2データ概要の表示
print('X2のデータ型', type(X2), ', 形状', X2.shape)
print('X2の要素1~3番目の値', X2[:3])【出力イメージ】

変数 X2 もNumPy配列であり、配列の中に100個のデータが入っています。
④$${E[X]}$$、$${V[X]}$$、$${E[X]^2+V[X]}$$、$${E[X^2]}$$ の計算
いよいよ核心に迫ります!
# 計算
X_mean = np.mean(X) # E[X] :Xの平均
X_var = np.var(X, ddof=0) # V[X] :Xの分散(不偏分散ではない)
X2_mean_est = X_mean**2 + X_var # E[X]^2 + V[X]
X2_mean = np.mean(X2) # E[X^2] :X^2の平均計算式の上から順に、$${E[X]}$$、$${V[X]}$$、$${E[X]^2+V[X]}$$、$${E[X^2]}$$を計算して、それぞれ新しい変数に計算結果を格納しています。
計算結果は、未だ表示しません!
⑤$${E[X]^2+V[X]}$$と$${E[X^2]}$$の比較、ヒストグラムの描画
# ヒストグラムをプロット(タイトルに各種数値を表示)
plt.figure(figsize=(6, 4))
plt.hist(X, bins='auto', ec='lightblue', density=True)
plt.title(f'$E[X]={X_mean:.4f},\ V[X]={X_var:.4f}$\n'
f'$E[X]^2+V[X]={X2_mean:.4f}\ vs.\ E[X^2]={X2_mean:.4f}$\n'
f'$Diff.:{X2_mean_est-X2_mean:.4f}$')
plt.show()まず plt.hist で、変数 X のヒストグラムを作成します。
次に plt.title で、ヒストグラムのタイトルに$${E[X]}$$、$${V[X]}$$、$${E[X]^2+V[X]}$$、$${E[X^2]}$$、差(Diff.)$${E[X]^2+V[X]-E[X^2]}$$を表示します。
さて、差(Diff.)$${E[X]^2+V[X]-E[X^2]}$$は 0 になったのでしょうか?
【出力イメージ】

やりました!
$${E[X]^2+V[X]}$$と$${E[X^2]}$$は同じ値になり、差がほぼ 0 になりました。
小数点の丸めなど、計算誤差が若干ありますが、両者は一致しているようです。

分散の公式(変形)のとおり、$${E[X]^2+V[X]=E[X^2]}$$になることを実データを用いて確認できました。
他のデータでも一致を確認できます。
Pythonを使える人は、ぜひ実験してみてください。
また、「Pythonで作成してみよう!」のコーナーで、他の分布に従う乱数の実験結果をご紹介いたします。

実践する
一緒に実験してみよう
「知る」の実験を別のデータで実施してみませんか?
この記事ではEXCEL、Pythonの実践をサポートいたします。
CSVファイルのダウンロード
こちらのリンクから乱数データのCSVファイルをダウンロードできます。
「EXCELで作成してみよう!」「Pythonで作成してみよう!」の利用データと同じ内容です。
【EXCELをお使いの方へ】
EXCELサンプルファイルに上記データを含めていますので、CSVファイルのダウンロードは不要です。
【Pythonをお使いの方へ】
Pythonコード内で乱数データを生成するので、ダウンロードしなくてもコードの実行は可能です。
電卓・手作業で作成してみよう!
今回の実験を手作業で遂行するのは少し厳しいかもしれません。
手作業で実験を再現する場合には、「EXCELで作成してみよう!」「Pythonで作成してみよう!」の内容をお読みいただき、CSVファイルのデータを用いて、計算作業を実施してください。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
実験用データシート
実験用データをEXCELに貼り付けして計算を行ったシートです。
6つの分布に従う乱数データと連続番号データの計7種類のデータを予めセットしています。

左下の【Xデータ】の箇所にデータを設定すると、左上の【計算】フォームで$${E[X]}$$、$${V[X]}$$、$${E[X]^2+V[X]}$$、$${E[X^2]}$$、差$${E[X]^2+V[X]-E[X^2]}$$を計算します。
薄ピンクの行が差を示しています。全て差が0になっています。
分散の公式は堅牢です!
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、さまざまな確率分布のデータで$${\boldsymbol{E[X]^2+V[X]=E[X^2]}}$$を確かめる実験に取り組みます。
①インポート
scipy.statsでさまざまな確率分布に従う乱数を生成しています。
import numpy as np
from scipy.stats import norm, binom, uniform, chi2, dweibull, f
import matplotlib.pyplot as plt②計算と描画処理を関数化
「実践する」のコードを関数化しました。
def X2_mean_calc(X):
# Xの平均と分散の計算
X_mean = np.mean(X)
X_var = np.var(X, ddof=0) # 不偏分散ではない
# E[X]^2 + V[X]の計算
X2_mean_est = X_mean**2 + X_var
# XからX^2データを作成
X2 = X**2
# X^2の平均の計算
X2_mean = np.mean(X2)
# Xのプロット
plt.figure(figsize=(6, 4))
plt.hist(X, bins='auto', ec='lightblue', density=True)
plt.title(f'$E[X]={X_mean:.4f},\ V[X]={X_var:.4f}$\n'
f'$E[X]^2+V[X]={X2_mean:.4f}\ vs.\ E[X^2]={X2_mean:.4f}$\n'
f'$Diff.:{X2_mean_est-X2_mean:.4f}$')
plt.show()③さまざまな分布で実験
各コードで確率分布に従う乱数を100個生成します。上記関数を呼び出して、実験(計算とグラフ描画)を行います。
先に結論を申し上げますと、公式どおり「$${E[X]^2+V[X]=E[X^2]}$$」が成り立っています。
■正規分布
# 正規分布 N(0, 1)
np.random.seed(1)
x = norm.rvs(loc=0, scale=1, size=100)
X2_mean_calc(x)
■二項分布
# 二項分布 Bin(100, 0.4)
np.random.seed(1)
x = binom.rvs(n=100, p=0.4, size=100)
X2_mean_calc(x)
■連続一様分布
# 連続一様分布 Uniform(-8, 12)
np.random.seed(1)
x = uniform.rvs(loc=-8, scale=20, size=100)
X2_mean_calc(x)
■カイ二乗分布
# カイ二乗分布 Χ^2(3)
np.random.seed(1)
x = chi2.rvs(df=3, size=100)
X2_mean_calc(x)
■ワイブル分布
# ワイブル分布
np.random.seed(1)
x = dweibull.rvs(c=3, size=100)
X2_mean_calc(x)
■F分布
# F分布 F(30, 20)
np.random.seed(1)
x = f.rvs(dfn=30, dfd=20, size=100)
X2_mean_calc(x)
■1~100の連続値
# 1~100の連続値
x = np.arange(1, 101)
X2_mean_calc(x)
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
公式・数式を実データで実験して確かめることって、なんだか楽しいです。
データをつくって、統計処理・分析処理をして、結果を評価するといった、一連のデータ分析を疑似体験している錯覚をおぼえるのです。
シリーズ化の予感!?
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
