
1-7 線形変換による平均・標準偏差 〜 パンの重さのばらつき
今回の統計トピック
確率変数の線形変換による平均と標準偏差の計算に挑みます!
加えて、平均・分散・標準偏差を計算してデータのばらつきを深掘りします。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
1変数記述統計の分野
問7 線形変換による平均・標準偏差(アメリカ主要都市の最低気温)
試験実施年月
統計検定2級 2019年6月 問3(回答番号8)
問題
公式問題集をご参照ください。
【注意】
今回は数式が多いです。イラスト多めでカモフラージュしています。
「いらすとや」さん、ありがとうございます!
3つの解き方を掲載しています。
ぜひお好みの解法を見つけてください!
解き方1(力技コース)
問題の概要
この問題の条件を整理しましょう。
【求めること】
・華氏($${F}$$)の平均($${\bar{F}}$$)と標準偏差($${s_F}$$)
【素材】
・データの個数は$${17}$$(表のアメリカの主要都市の数)
・摂氏($${C}$$)から華氏($${F}$$)への変換式は、$${F=1.8C+32}$$
・摂氏($${C}$$)でのデータの平均($${\bar{C}}$$)は$${2.4}$$、標準偏差($${s_C}$$)は$${7.0}$$
・この問題の標準偏差は、不偏分散の正の平方根

平均
平均はデータを全て足して、データ個数で割った値です。
この問題では、表の17都市の華氏の値を合計してから17で割ると華氏の平均が求まります。
力技で計算してみましょう。
$${(33.8+21.2+42.8+39.2+21.2+24.8+30.2+39.2+30.2+30.2+39.2+23.0+42.8+71.6+44.6+50.0+32.0)\div 17 \\= 36.23 \cdots}$$
標準偏差
この問題の標準偏差は「不偏分散の正の平方根」です。
まず、華氏の不偏分散を求めましょう。
次の順序で不偏分散を計算できます。
・華氏の各データからそれぞれ平均を引く(偏差の算出)
・上記(偏差)を二乗する
・上記をデータ数17個分計算して合計する(偏差平方和の算出)
・上記の合計(偏差平方和)を「データ数$${17-1}$$」で割る
最後の計算結果が「不偏分散」です。
続いて標準偏差は次のように計算できます。
・不偏分散の平方根(√)
力技で計算してみましょう。
平均は解答選択肢の$${36.3}$$を用いてみましょう。
式が長くなるので、まず、不偏分散から求めます。
$${ \{ (33.8 - 36.3 )^2 + (21.2 - 36.3 )^2 + (42.8 - 36.3 )^2 + (39.2 - 36.3 )^2 + (21.2 - 36.3 )^2 + (24.8 - 36.3 )^2 + (30.2 - 36.3 )^2 + (39.2 - 36.3 )^2 + (30.2 - 36.3 )^2 + (30.2 - 36.3 )^2 + (39.2 - 36.3 )^2 + (23.0 - 36.3 )^2 + (42.8 - 36.3 )^2 + (71.6 - 36.3 )^2 + (44.6 - 36.3 )^2 + (50.0 - 36.3 )^2 + (32.0 - 36.3 )^2 \} \div (17-1) \\ = 157.12 \cdots }$$
続いて、標準偏差を求めます。
$${\sqrt{157.12} = 12.53 \cdots}$$
以上から、華氏の平均$${\bar{F}}$$は約$${36.23}$$、標準偏差$${s_F}$$は約$${12.53}$$です。
(おわり)
ひと山超えました。
お疲れ様です。

解き方2の準備
平均の式表現
この問題の華氏の平均$${\bar{F}}$$を計算式で示すと次のようになります。
$$
\bar{F} = \displaystyle \cfrac{1}{17}\sum^{17}_{i=1} F_i
= \displaystyle \cfrac{1}{17}\sum^{17}_{i=1} (1.8 C_i + 32)
$$
$${\displaystyle \cfrac{1}{17}\sum^{17}_{i=1} F_i}$$は、華氏$${F}$$をデータ$${1}$$番目の$${F_1}$$からデータ$${17}$$番目の$${F_{17}}$$まで全て足しあげて、データ個数$${17}$$で割る、という意味です。
力技のグレーの部分と同じ意味を示す式です。
また、$${i}$$番目の華氏$${F_i}$$は$${i}$$番目の摂氏$${C_i}$$との関係で$${F_i=1.8 C_i + 32}$$ですので、$${\displaystyle \cfrac{1}{17}\sum^{17}_{i=1} (1.8 C_i + 32)}$$となります。
標準偏差の式表現
この問題の華氏の標準偏差$${s_F}$$を計算式で示すと次のようになります。
$$
\begin{align*}
s_F &= \displaystyle \sqrt{ \cfrac{1}{16}\sum^{17}_{i=1} (F_i-\bar{F})^2} \\
&= \displaystyle \sqrt{ \cfrac{1}{16} \sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32) \}^2}
\end{align*}
$$
$${\displaystyle \sqrt{ \cfrac{1}{16}\sum^{17}_{i=1} (F_i-\bar{F})^2}}$$は標準偏差の計算手順そのものです。
力技のグレーの部分と同じ意味を示す式です。
ちなみに、平方根を取る前の値、$${\cfrac{1}{16}\sum^{17}_{i=1} (F_i-\bar{F})^2}$$を不偏分散$${s^2_F}$$と呼びます。
$${F_i=1.8 C_i + 32}$$、$${\bar{F}=1.8 \bar{C} + 32}$$ですので、$${ \displaystyle \sqrt{ \cfrac{1}{16} \sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32) \}^2} }$$となります。
ひと休みしましょう。

解き方2(式展開ゆっくりコース)
平均
次の式から展開を始めます。
$$
\bar{F} = \displaystyle \cfrac{1}{17}\sum^{17}_{i=1} (1.8 C_i + 32)
\tag{1.1}
$$
$${\sum^{17}_{i=1} (1.8 C_i + 32)}$$の部分に注目します。
データ$${i=1~17}$$番目の摂氏のデータ$${C_i}$$について、$${(1.8 C_i + 32)}$$を合計します。
こんな感じです。
$$
\left.
\begin{align*}
&1.8 \times C_1 + 32 \\
+&1.8 \times C_2 + 32 \\
&(省略) \\
+&1.8 \times C_{16} + 32 \\
+&1.8 \times C_{17} + 32 \\
\end{align*}
\right\} 全部で17個を足す
\tag{1.2}
$$
この内容を1つの式にまとめます。
$$
1.8 \times (C_1 + C_2 + \cdots + C_{16} + C_{17}) + 17 \times 32
\tag{1.3}
$$
$${(C_1 + C_2 + \cdots + C_{16} + C_{17})}$$は$${\sum^{17}_{i=1} C_i}$$ですので、次のように書けます。
$$
\displaystyle
1.8 \times \sum^{17}_{i=1} C_i + 17 \times 32
\tag{1.4}
$$
式$${(1.1)}$$の$${\sum^{17}_{i=1} (1.8 C_i + 32)}$$を式$${(1.4)}$$で置き換えます。
$$
\displaystyle
\bar{F} = \cfrac{1}{17} \left( 1.8 \times \sum^{17}_{i=1} C_i + 17 \times 32 \right)
\tag{1.5}
$$
$${()}$$を外してこの式を展開します。
$$
\begin{align*}
\displaystyle
\bar{F} &= \cfrac{1}{17} \times 1.8 \times \sum^{17}_{i=1} C_i + \cfrac{1}{17} \times 17 \times 32 \\
&= 1.8 \times \cfrac{1}{17} \times \sum^{17}_{i=1} C_i + \cancel{\cfrac{1}{17}} \times \cancel{17} \times 32 \\
&= 1.8 \times \cfrac{1}{17} \sum^{17}_{i=1} C_i + 32
\end{align*}
\tag{1.6}
$$
$${\cfrac{1}{17} \sum^{17}_{i=1} C_i}$$は摂氏の平均$${\bar{C}}$$ですので、次のように書けます。
$$
\bar{F} = 1.8 \bar{C} + 32
\tag{1.7}
$$
摂氏の平均$${\bar{C}=2.4}$$を代入して解きます。
$$
\bar{F} = 1.8 \times 2.4 + 32 = 36.32 \fallingdotseq 36.3
\tag{1.8}
$$
標準偏差
次の式から展開を始めます。
$$
\displaystyle
s_F = \sqrt{ \cfrac{1}{16} \sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32) \}^2}
\tag{2.1}
$$
まず、$${\sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32)\}^2}$$の部分に注目して、$${\{\}}$$の中を整理します。
$$
\begin{align*}
&\sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32)\}^2\\
=&\sum^{17}_{i=1} (1.8 C_i + 32-1.8 \bar{C} - 32)^2\\
=&\sum^{17}_{i=1} (1.8 C_i -1.8 \bar{C} )^2\\
=&\sum^{17}_{i=1} \{1.8\times(C_i -\bar{C} )\}^2\\
=&\sum^{17}_{i=1} (1.8^2 \times (C_i -\bar{C} )^2 )
\end{align*}
\tag{2.2}
$$
$${\sum^{17}_{i=1} (1.8^2 \times (C_i -\bar{C} )^2)}$$において、$${1.8^2}$$は摂氏のデータ$${i}$$($${1}$$番目から$${17}$$番目)の値に関わらず一定です。
そこで、
$${(1.8^2 \times (C_1 -\bar{C} )^2) + (1.8^2 \times (C_2 -\bar{C} )^2) + \cdots + (1.8^2 \times (C_{17} -\bar{C} )^2) }$$
を
$${1.8^2 \times \{ (C_1 -\bar{C} )^2 + (C_2 -\bar{C} )^2 + \cdots + (C_{17} -\bar{C} )^2 \}}$$
へ変形します。
また、$${\{ (C_1 -\bar{C} )^2 + (C_2 -\bar{C} )^2 + \cdots + (C_{17} -\bar{C} )^2 \}}$$は、$${\sum^{17}_{i=1} (C_i -\bar{C} )^2}$$のことです。
よって、
$$
\sum^{17}_{i=1} (1.8^2 \times (C_i -\bar{C} )^2) \\
=1.8^2 \times \sum^{17}_{i=1} (C_i -\bar{C} )^2
\tag{2.3}
$$
式$${(2.1)}$$の$${\sum^{17}_{i=1} \{(1.8 C_i + 32)-(1.8 \bar{C} + 32)\}^2}$$を式$${(2.3)}$$で置き換えます。
$$
\displaystyle
s_F = \sqrt{ \cfrac{1}{16} \left\{1.8^2 \times \sum^{17}_{i=1} (C_i -\bar{C} )^2 \right\}}
\tag{2.4}
$$
$${\{\}}$$を外して整理します。
$$
\displaystyle
s_F = \sqrt{ 1.8^2 \times \cfrac{1}{16} \sum^{17}_{i=1} (C_i -\bar{C} )^2 }
\tag{2.5}
$$
$${\cfrac{1}{16} \sum^{17}_{i=1} (C_i -\bar{C} )^2 }$$は摂氏の不偏分散$${s^2_C}$$ですので、次のように書けます。
$$
s_F = \sqrt{1.8^2 \times s^2_C}
\tag{2.6}
$$
平方根(√)の中を整理します。
$$
\begin{align*}
s_F &= \sqrt{ (1.8 \times s_C)^2 }
&= 1.8 \times s_C
\end{align*}
\tag{2.7}
$$
摂氏の標準偏差$${s_C=7.0}$$を代入して解きます。
$$
s_F = 1.8 \times 7.0 = 12.6
\tag{2.8}
$$
以上から、華氏の平均$${\bar{F}}$$は約$${36.3}$$、標準偏差$${s_F}$$は約$${12.6}$$です。
総和Σのメモ
$${\sum^N_{i=1} ax_i+b}$$について、次のことが分かりました。
$${\sum^N_{i=1} (ax_i+b)=\sum^N_{i=1} ax_i + \sum^N_{i=1}b}$$
$${\sum^N_{i=1} ax_i = a \times \sum^N_{i=1} x_i}$$
$${\sum^N_{i=1}b=N \times b}$$
(おわり)
やり切りました!やったー!やっほー!

まとめ
この問題では、変換公式$${F=1.8C+32}$$を用いて、摂氏$${C}$$のデータを華氏$${F}$$へ線形変換するときの華氏の平均$${\bar{F}}$$と標準偏差$${s_F}$$を求めました。
華氏の平均$${\bar{F}}$$は、変換公式の$${C}$$を摂氏の平均$${\bar{C}}$$に置き換えた「$${\bar{F}=1.8\bar{C}+32}$$」になりました。
摂氏データの平均をそのまま変換公式に当てはめて、華氏データの平均に変換できることが分かりました。
華氏の標準偏差$${s_F}$$は、変換公式のうち、摂氏データの係数と変数$${1.8C}$$の$${C}$$を摂氏の標準偏差$${s_C}$$に置き換えた「$${s_F=1.8 s_C}$$」になりました。
摂氏データの標準偏差を変換公式の摂氏の係数(の絶対値)と変数に当てはめて、華氏データの標準偏差に変換できることが分かりました。
また、標準偏差の変換の際、変換公式の定数$${32}$$は影響しないことが分かりました。
解き方3(公式利用コース)
最後に確率変数の線形変換の公式を利用して解きます。
【確率変数の線形変換の公式】
平均=期待値
$${E[aX+b]=aE[X]+b}$$
分散
$${V[aX+b]=a^2V[X]}$$
標準偏差
$${SD[aX+b]=\sqrt{a^2V[X]}=|a|SD[X]}$$
摂氏から華氏の変換公式$${F=1.8C+32}$$、摂氏の平均$${E[C]=2.4}$$、標準偏差$${SD[C]=7.0}$$を、上述の「確率変数の線形変換の公式」に当てはめて、計算します。
平均=期待値$${E[F]=E[1.8C+32]=1.8E[C]+32=1.8\times2.4+32=36.32}$$
標準偏差$${SD[F]=SD[1.8C+32]=|a|SD[C]=1.8\times7.0=12.6}$$
なお、確率変数の線形変換は、記事「5-8 線形な変数変換、共分散、相関係数」にて総合的に取り組みます。
解答
④です。
難易度 ふつう
・知識:平均、不偏分散、標準偏差
・計算力:電卓(高)、または、数式(中)
・時間目安:2分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は平均・分散・標準偏差を求めてみましょう。
ここでは、例題用の仮設の数値を用います。

10個のパンの重さ(単位:g)の例題データを利用します。
100.0, 101.4, 103.2, 99.7, 98.4, 102.7, 99.1, 102.5, 100.3, 103.6
平均・分散・標準偏差の計算
📕公式テキスト:1.3.1 平均・分散・標準偏差(15ページ~)
平均
平均は$${n}$$個のデータ$${x_i \quad (i=1, 2, \cdots, n)}$$の値の合計をデータ個数で割って算出します。
【計算式】
$$
平均\bar{x} = \cfrac{1}{n} (x_1+x_2+\cdots +x_n) = \cfrac{1}{n} \sum^n_{i=1} x_i
$$
例題のパンの重さの平均は次のように計算します。
$$
\begin{align*}
&パンの重さの平均\bar{x}\\
&=\cfrac{1}{データ数10} \times (100.0+101.4+103.2+99.7+ 98.4+102.7+99.1+102.5+100.3+103.6)\\
&=101.090\cdots = 101.09
\end{align*}
$$
分散の計算
分散には主に2つの計算方法があります。
1つ目は記述統計の文脈で使われることの多い「分散」、2つ目は推測統計の文脈で使われることの多い「不偏分散」です。
「分散」は学校教育で取り扱われることが多く、授業で実際に計算した方も多いのではないでしょうか。
「不偏分散」は標本調査などの場面で取り扱われます。不偏分散の期待値は母集団の分散(母分散)と等しい性質を持っています。
両者の計算の違いは、分数の分母が$${\boldsymbol{n}}$$か$${\boldsymbol{n-1}}$$かの違いです。
①分散
分散は$${n}$$個のデータ$${x_i \quad (i=1, 2, \cdots, n)}$$、平均$${\bar{x}}$$を用いて、次のように計算します。
【計算式】
$$
\begin{align*}
\displaystyle
分散s^2 &= \cfrac{1}{n} \{ (x_1- \bar{x})^2+(x_2- \bar{x})^2+\cdots + (x_n- \bar{x})^2 \} \\
&= \cfrac{1}{n} \sum^n_{i=1} (x_i - \bar{x})^2
\end{align*}
$$
例題のパンの重さの分散は次のように計算します。
$$
\begin{align*}
&パンの重さの分散 s^2 \\
&= \cfrac{1}{データ数10} \times \{ (100.0-101.09)^2+(101.4-101.09)^2+(103.2-101.09)^2+(99.7-101.09)^2+ (98.4-101.09)^2+(102.7-101.09)^2+(99.1-101.09)^2+(102.5-101.09)^2+(100.3-101.09)^2+(103.6-101.09)^2 \} \\
&= 3.036 \cdots = 3.04
\end{align*}
$$
②不偏分散
不偏分散は$${n}$$個のデータ$${x_i \quad (i=1, 2, \cdots, n)}$$、平均$${\bar{x}}$$を用いて、次のように計算します。
【計算式】
$$
\begin{align*}
\displaystyle
不偏分散\hat{\sigma}^2
&= \cfrac{1}{n-1} \{ (x_1- \bar{x})^2+(x_2- \bar{x})^2+\cdots + (x_n- \bar{x})^2 \} \\
&= \cfrac{1}{n-1} \sum^n_{i=1} (x_i - \bar{x})^2
\end{align*}
$$
例題のパンの重さの不偏分散は次のように計算します。
$$
\begin{align*}
&パンの重さの不偏分散 \hat{\sigma}^2 \\
&= \cfrac{1}{データ数10-1} \times \{ (100.0-101.09)^2+(101.4-101.09)^2+(103.2-101.09)^2+(99.7-101.09)^2+ (98.4-101.09)^2+(102.7-101.09)^2+(99.1-101.09)^2+(102.5-101.09)^2+(100.3-101.09)^2+(103.6-101.09)^2 \} \\
&= 3.374 \cdots = 3.37
\end{align*}
$$
標準偏差
標準偏差は分散は$${n}$$個のデータ$${x_i \quad (i=1, 2, \cdots, n)}$$、平均$${\bar{x}}$$、分散$${s^2}$$または不偏分散$${\hat{\sigma}^2}$$を用いて、次のように計算します。
【計算式】
$$
\displaystyle
標準偏差(分散)s = \sqrt{s^2} = \sqrt{ \frac{1}{n} \sum^n_{i=1} (x_i - \bar{x})^2}\\
標準偏差(不偏分散)\hat{\sigma} = \sqrt{\hat{\sigma}^2} = \sqrt{ \frac{1}{n-1} \sum^n_{i=1} (x_i - \bar{x})^2}
$$
例題のパンの重さの標準偏差は次のように計算します。
$$
\begin{align*}
パンの重さの標準偏差(分散)s&=\sqrt{3.04}
&=1.743 \cdots = 1.74\\
パンの重さの標準偏差(不偏分散)\hat{\sigma}&=\sqrt{3.37}
&=1.835 \cdots = 1.84
\end{align*}
$$

平均・分散・標準偏差の意味すること
概要
平均は「全データの重心」として位置づけられます。
分散・標準偏差は「データの散らばり具合」の指標です。
ケース
パンの重さについて、2つのケースを見てみましょう。
1つは今まで使用した「データ1」です。
平均は 101.09g です。

もう1つは初登場の「データ2」です。
平均はデータ1と同じで、101.09g です。

「重さ」の列に10個分のパンの重さを記載しています。
データ2の重さは平均値よりも上下に大きく乖離しています。
分散・標準偏差の欄を見ると、データ2の値は大きくなっています。
散布図
データの散らばり具合を散布図で可視化してみましょう。

赤い線は平均値です。
データ1の各点は平均値の近くにあります。
データ2の各点はデータ1と比べて、平均値から離れている点が多いです。
どちらのショップで買いたいですか?
ベーカリーショップの手作りパンの重さにばらつきがあったと仮定します。
基準値が 100g の場合、どちらのショップを選びますか?
両ショップとも基準値を下回るデータが見られます。
ショップでは、100g未満にならないような対策が必要かもしれません。
データ2のショップは基準値から10%以上乖離するデータがあります。
ショップでは、許容範囲を超えるようであれば、原因を明らかにして対策を講ずる必要があるかもしれません。
まとめ
このように、分散・標準偏差は、平均値からの乖離の度合い=散らばり具合を示す指標です。
分散・標準偏差の違いは、単位にあります。
分散は計算式で二乗しているので、データの単位の二乗の単位になってしまいます。$${g^2}$$です。
標準偏差は分散の平方根なので、データの単位が元のデータの単位と同じになります。$${g}$$です。
標準偏差を標準誤差として扱う時、「平均値 ± 標準偏差」のように加減算できるのは単位が揃っているからです。
分散は統計学のさまざまなシーンで活用される統計量です。
締めます
平均・分散・標準偏差はデータの分布を表す基本的かつ重要な指標です。
さささっと計算できるようになるといいかもです。
政府提供の統計の学び場
総務省統計局と統計研究研修所が共同運営する「なるほど統計学園」では、分散・標準偏差のことを「データの特徴を捉える上級編の扱い」で取り扱っています。
ぜひWebサイトに訪れて、政府の統計ノウハウを体感してみてください。
もっと本格的な統計の学びの場もあります。
その名も「データサイエンス・スクール」(総務省統計局)。
オンライン教材、実力テストなどのコンテンツが揃っている感じです。
そしてキャラクターのネーミングがw
次は平均と正規分布に関するページです。参考にどうぞ。
実践する
平均・分散・標準偏差を計算してみよう
今回は例題データをコピペして計算してみましょう。
電卓・手作業で作成してみよう!
上述の方法でデータを取得して、電卓やそろばんをはじいて、手作業で計算してみましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

平均・分散・標準偏差
関数が揃っています。
・平均:AVERAGE関数
・分散:VAR.P関数
・不偏分散:VAR.S関数
・標準偏差(分散):STDEV.P関数
・標準偏差(不偏分散):STDEV.S関数
いずれの関数も、引数に計算対象のデータ値またはデータ範囲を指定します。
散布図
対象データの範囲を指定して、「挿入」メニューからグラフの右下隅の矢印を押し、「グラフの挿入」画面で「散布図」を選びます。
次の図では、データ1の重さデータの散布図を作る目的で、「セルC4~C13」を選択してから、「挿入」メニュー以降の操作をしています。

EXCELサンプルファイルでは、次の表に関数を利用した計算式を設定しています。
また、散布図の作成も行っています。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、平均・分散・標準偏差を計算します。
①ライブラリのインポート
NumPyを使用して平均・分散・標準偏差を計算します。
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②サンプルデータの読み込み
2つのリストを作成します。
# 例題データ1、2
pan1 = [100.0, 101.4, 103.2, 99.7, 98.4, 102.7, 99.1, 102.5, 100.3, 103.6]
pan2 = [100.0, 107.4, 110.8, 92.1, 98.1, 102.7, 95.1, 102.5, 96.0, 106.2]
print(type(pan1), type(pan2))
print(pan1)
print(pan2)
出力イメージ
<class 'list'> <class 'list'>
[100.0, 101.4, 103.2, 99.7, 98.4, 102.7, 99.1, 102.5, 100.3, 103.6]
[100.0, 107.4, 110.8, 92.1, 98.1, 102.7, 95.1, 102.5, 96.0, 106.2]③平均・分散・標準偏差の計算
NumPyのmean、var、stdを使用しています。
var、stdの引数ddof=1を設定すると、不偏分散を計算できます。
print('-'*10, '分散(分母がn)', '-'*10)
print('平均 :{:.4f}'.format(np.mean(pan1)))
print('分散 :{:.4f}'.format(np.var(pan1)))
print('標準偏差:{:.4f}'.format(np.std(pan1)))
print('-'*10, '不偏分散(分母がn-1)', '-'*10)
print('平均 :{:.4f}'.format(np.mean(pan1)))
print('不偏分散:{:.4f}'.format(np.var(pan1, ddof=1)))
print('標準偏差:{:.4f}'.format(np.std(pan1, ddof=1)))
出力イメージ
---------- 分散(分母がn) ----------
平均 :101.0900
分散 :3.0369
標準偏差:1.7427
---------- 不偏分散(分母がn-1) ----------
平均 :101.0900
不偏分散:3.3743
標準偏差:1.8369④Pandasのdescribe
std(標準偏差)の値は不偏分散にもとづきます。
pd.DataFrame(pan1).describe()
⑤散布図の表示
pan1とpan2をプロットします。
x = range(1,11,1)
pan1_mean = np.mean(pan1)
plt.figure(figsize=(4, 4))
plt.ylim(90, 115)
plt.axhline(pan1_mean, ls='--', lw=0.5, c='tomato')
plt.scatter(x, pan1, s=100, c='lightblue', ec='darkblue',
lw=0.7, alpha=0.5, label='パン1(g)')
plt.scatter(x, pan2, s=100, c='pink', ec='red',
lw=0.7, alpha=0.5, label='パン2(g)')
plt.title('散布図:パン1,パン2')
plt.text(9.2, pan1_mean+0.1, 'mean', fontfamily='serif', color='tomato')
plt.legend(loc='best')
# plt.savefig('./scatter.png') # グラフ画像ファイルの保存
plt.show()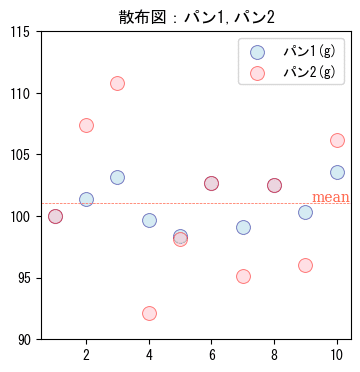
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
確率変数の線形変換はなかなか難しいテーマです。
なるべく難しい計算式を使わないで、直感的にイメージできるように、工夫したいと思いつつ、なかなか説明が難しいです。
統計検定2級の本試験では公式を用いてすらすら解けるようなスピード感が必要だったりします。
公式(数式)に真正面から取り組むことも大切なのです。
ところで、ワールド・ベースボール・クラシック(WBC)で日本チームが優勝しました!
おめでとうございます!やったね!

最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
