
4-1 積事象の確率 ~ 条件付き確率&確率の乗法定理を四角形の面積で計算
今回の統計トピック
条件付き確率の定義と確率の乗法定理を利用して、積事象の確率を求める問題に取り組みます。
さらに類似問題を解いて復習します。かわいいお店番が登場します!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率の分野
問1 積事象の確率(試験対策講座の受講)
試験実施年月
統計検定2級 2019年11月 問8(回答番号12)
問題
公式問題集をご参照ください。
解き方
題意
次の条件で、受験者のうち「講座を受講する」と同時に「試験に合格する」確率を求めます。
【講座を受講する確率】
・受験者のうち講座を受講する確率: 20%
【試験に合格する確率】
・講座を受講する者のうち試験に合格する確率:70%
・講座を受講しない者のうち試験に合格する確率:30%
図で解く
横1・縦1・面積1の正方形を利用して、受験者のうち「講座を受講する」と同時に「試験に合格する」割合=確率を求めます。

①受験者が「講座を受講する」確率は 0.2 。
②「講座を受講する」場合に「試験に合格する」確率は 0.7 。
受験者のうち「講座を受講する」と同時に「試験に合格する」確率は、①の確率 0.2 と②の確率 0.7 を掛け算(積)して求めます。
答えは 0.14 です。
確率の乗法定理の公式で解く
まず、事象を次のように定めます。
・講座を受講する事象:$${A}$$
・試験に合格する事象:$${B}$$
求める確率は、受験者のうち「講座を受講する事象$${A}$$」と同時に「試験に合格する事象$${B}$$」の起きる積事象の確率 $${P(A \cap B)}$$ です。
問題文より、次の確率を得ます。
・「講座を受講する事象$${A}$$」の確率:$${P(A)=0.2}$$
・「講座を受講する事象$${A}$$」の場合に「試験に合格する事象$${B}$$」の起きる条件付き確率:$${P(B \mid A)=0.7}$$
これらの内容を確率の乗法定理に当てはめて、確率を計算します。
【確率の乗法定理】
$$
P(A \cap B) = P(A)\ P(B \mid A)
$$
【計算過程】
$$
P(A \cap B)=0.2\times0.7=0.14\\
$$
答えは 0.14 です。
解答
① 0.14 です。
難易度 やさしい
・知識:積事象の確率、条件付き確率、確率の乗法定理
・計算力:数式組み立て(低)、電卓(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、類似問題を一緒に解いていきましょう!
事象と確率
📕公式テキスト:2.1 事象と確率(55ページ~)
類似問題
くじ付き菓子の購入者について考えます。
通常は 20% の確率でくじが当たります。
お店番と仲良しの客の場合は 80% の確率でくじが当たります。
購入者がお店番と仲良しの確率は 30% です。
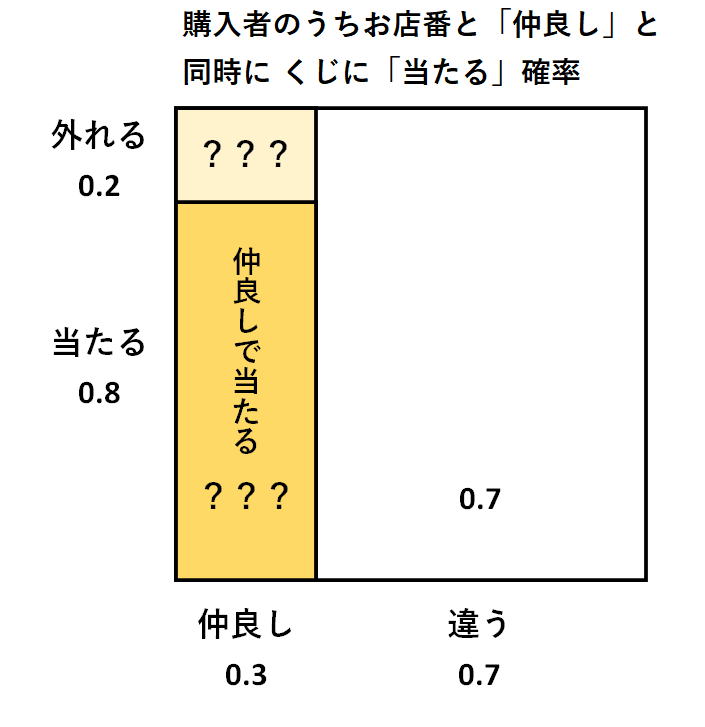
くじ付き菓子の購入者から無作為に1人を選んだとき、その人がお店番と仲良しで、くじに当たっている確率は何%でしょう。

事象と確率
店番と仲良しである事象を$${A}$$、くじに当たる事象を$${B}$$とします。
確率は$${P}$$の記号を用います。
店番と仲良しである事象の確率は$${P(A)}$$と表し、確率が 0.3 なので、$${P(A)=0.3}$$と表します。
図にします。

条件付き確率
店番と仲良しである場合にくじに当たる確率は$${P(B \mid A)}$$と表します。
確率が 0.8 なので、$${P(B \mid A)=0.8}$$です。
$${P( くじに当たる \mid 店番と仲良しである)}$$という意味であり、「店番と仲良し」という事象が起きる条件のときに「くじに当たる」確率です。
条件付き確率と呼びます。
図にします。
「仲良し」を 1 としたときの「当たる」確率が 0.8 です。

積事象の確率
店番と仲良しでくじに当たる事象は、「店番と仲良し」という事象$${A}$$と「くじに当たる」という事象$${B}$$が同時に起きる事象です。
このように、ある事象とある事象が同時に起きる事象は積事象です。
$${A \cap B}$$と表します。
この積事象が起きる確率は$${P(A \cap B)}$$と表します。
設問の問いは、積事象の確率$${P(A \cap B)}$$を求めることです。
図にします。
条件付き確率の公式
唐突ですが、条件付き確率の公式です。
いままでに出てきた役者が勢ぞろいします。
$$
P(B \mid A) = \cfrac{P(A \cap B) }{P(A)}
$$
言葉にしてみます。
$$
P( 店番と仲良しを条件として、くじに当たる) \\
\\
=\cfrac{P(店番と仲良し、同時に、くじに当たる)}{P(店番と仲良し)}
$$
図にします。

確率の乗法定理
条件付き確率の定義を変形して、確率の乗法定理を導きます。
$$
P(A \cap B)=P(A)\ P(B \mid A)
$$
言葉にしてみます。
$$
\begin{align*}
&P(店番と仲良し、同時に、くじに当たる)\\
&=P(店番と仲良し) \times P( 店番と仲良しを条件として、くじに当たる) \\
&=0.3 \times 0.8 =0.24
\end{align*}
$$
図にします。

計算結果は 0.24 です。
くじ付き菓子の購入者から無作為に1人を選んだとき、その人がお店番と仲良しで、くじに当たっている確率は24%です。
(おわり)

公式のまとめ
条件付き確率
$${P(B \mid A) = \cfrac{P(A \cap B) }{P(A)}}$$
確率の乗法定理
$${P(A \cap B)=P(A)\ P(B \mid A)}$$
(参考)確率の加法定理
$${P(A \cup B)=P(A)+P(B)-P(A \cap B)}$$
実践する
今回はお休みです。
電卓・手作業で作成してみよう!
今回はお休みです。
EXCELで作成してみよう!
今回はお休みです。
EXCELサンプルファイルのダウンロード
今回はファイル提供はありません。
Pythonで作成してみよう!
今回はお休みです。
Pythonサンプルファイルのダウンロード
今回はファイル提供はありません。
おわりに
「確率」のテーマが始まりました。
このテーマではさまざまな公式・計算式が並びます。
基本的な公式ですので、試験対策の観点で覚えておくのがおすすめです。
確率変数や分布の挙動が面白いテーマについては、PythonやEXCELで動きを追体験して、確率・分布の気持ちに寄り添えるように工夫したいと思います。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
