
6-6 分散・共分散・相関係数 ~ 難関問題を解いて、データと平均の相関係数の謎を追う
今回の統計トピック
相関係数が同じである3つのデータについて、3データ平均vs各データの相関係数がどのような値になるのかを考える問題です。
問題集では数式を解いて相関係数を「理論的に」計算しています。
あわせて実際にデータを作り、実データの相関係数を「実践的に」計算して、理論に迫ります!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
標本分布の分野
問6 分散・共分散・相関係数(データなし)
試験実施年月
統計検定2級 2016年11月 問8(回答番号15)
問題
公式問題集をご参照ください。
解き方
題意
関連する複数の確率変数の分散、共分散、相関係数の関係の理解を確認する問題です。
次の条件のとき、確率変数$${X_1}$$と確率変数$${Y}$$の相関係数を求めます。
・ある3つデータを標準化したものを$${X_1, X_2, X_3}$$とする。
・平均$${Y=(X_1+X_2+X_3)/3}$$とする。
・相関係数$${r[X_1, X_2]=r[X_2, X_3]=r[X_1, X_3]=0.5}$$である。
期待値・分散・共分散・相関係数の公式をフル活用して問題を解きます。
なお、各種公式は記事「5-8 線形な変数変換、共分散、相関係数」にまとめて掲載しています。
こちらもあわせてご覧くださいね!

ステップ1:相関係数の公式に当てはめる
相関係数$${r[X,Y]=\cfrac{\mathrm{Cov}[X,Y]}{\sqrt{V[X]V[Y]}}}$$
相関係数の公式に当てはめると、相関係数$${r[X_1,Y]=\cfrac{\mathrm{Cov}[X_1,Y]}{\sqrt{V[X_1]\ V[Y]}}}$$です。
必要なピース「分散$${V[X_1]}$$」「分散$${V[Y]}$$」「共分散$${\mathrm{Cov}[X_1,Y]}$$」を愚直に計算して、相関係数を求めます。

ステップ2:分散$${\boldsymbol{V[X_1]}}$$の計算
問題文より「$${X_1}$$は標準化されている」ので、$${V[X_1]=1}$$です。
標準化は、確率変数$${X}$$に魔法「$${Z=(X-\mu)/\sigma}$$」🧙をかけて、平均0、分散1にすることでした。

ステップ3:分散$${\boldsymbol{V[Y]}}$$の計算
計算途中で公式等を挟みます。
--- 計算開始 ---
$$
\begin{align*}
V[Y]&=V[(X_1+X_2+X_3)/3]\\
\\
&=V \left[\cfrac{1}{3}\ (X_1+X_2+X_3) \right]\\
\\
&= \left( \cfrac{1}{3} \right)^2 V[X_1+X_2+X_3]\\
\\
&= \cfrac{1}{9}\ V[X_1+X_2+X_3]\
\end{align*}
$$
--- 計算中断 ---
確率変数どうしが独立でない場合の「確率変数の和の分散の公式」を利用して、分散$${\frac{1}{9} V[X_1+X_2+X_3]}$$を分解します。
■分散の演算の公式(3つ以上の確率変数の和、独立でない場合)
$${V[X_1+X_2+\cdots + X_n]}$$
$${=V[X_1]+V[X_2]+\cdots +V[X_n]+2\displaystyle \sum^{n-1}_{i=1} \sum^n_{j=i+1} \mathrm{Cov}[X_i,\ X_j]}$$
■分散の演算の公式(3つの確率変数の和、独立でない場合)
$${V[X_1+X_2+X_3]}$$
$${=V[X_1]+V[X_2]+V[X_3]}$$
$${\ +2\text{Cov}[X_1, X_2] +2\text{Cov}[X_1, X_3]+2\text{Cov}[X_2, X_3]}$$
【3つの確率変数の和の分散$${V[X_1+X_2+X_3]}$$の公式の記憶法】
確率変数$${X_1, X_2, X_3}$$の分散共分散行列っぽいマトリクスを書いて、出現する分散と共分散を合計すると$${V[X_1]+V[X_2]+V[X_3]+2\mathrm{Cov}[X_1, X_2]+2\mathrm{Cov}[X_1, X_3]+2\mathrm{Cov}[X_2, X_3] }$$になります。
$$
\begin{array}{c|c|c|c}
& X_1 & X_2 & X_3 \\
\hline
X_1 & V[X_1] & \text{Cov}[X_1, X_2] & \text{Cov}[X_1, X_3] \\
X_2 & \text{Cov}[X_1, X_2] & V[X_2] & \text{Cov}[X_2, X_3] \\
X_3 & \text{Cov}[X_1, X_3] & \text{Cov}[X_2, X_3] & V[X_3] \\
\end{array}
$$
--- 計算再開 ---
$$
\begin{align*}
V[Y]&=\cfrac{1}{9}\ V[X_1+X_2+X_3]\\
\\
&=\cfrac{1}{9}\ ( V[X_1]+V[X_2]+V[X_3] \\
\\
&\ +2\mathrm{Cov}[X_1, X_2]+2\mathrm{Cov}[X_2, X_3]+2\mathrm{Cov}[X_1, X_3] )\\
\end{align*}
$$
--- 計算中断 ---
上記の式に含まれる分散と共分散を計算します。
まず$${X_1,X_2,X_3}$$の分散は、問題文より「$${X_1,X_2,X_3}$$は標準化されている」ので、$${V[X_1]=V[X_2]=V[X_3]=1}$$です。
続いて$${X_1,X_2,X_3}$$の共分散を次のように計算します。
まず問題文より「相関係数$${r[X_1, X_2]=r[X_2, X_3]=r[X_1, X_3]=0.5}$$」が分かります。
次に$${V[X_1]=V[X_2]=V[X_3]=1}$$です。
相関係数$${r[X_1, X_2]=\cfrac{\mathrm{Cov}[X_1, X_2]}{\sqrt{V[X_1]V[X_2]}}=0.5}$$に分散の値を当てはめると、
$$
\begin{align*}
r[X_1, X_2]&=\cfrac{\mathrm{Cov}[X_1, X_2]}{\sqrt{1\times1}}=\mathrm{Cov}[X_1, X_2]=0.5
\end{align*}
$$
同様に計算して、共分散$${\mathrm{Cov}[X_1, X_2]=\mathrm{Cov}[X_2, X_3]=\mathrm{Cov}[X_1, X_3]=0.5}$$になります。
分散・共分散が出揃いましたので、$${V[Y]}$$の計算に戻りましょう。
--- 計算再開 ---
$$
\begin{align*}
V[Y] &=\cfrac{1}{9}\ ( V[X_1]+V[X_2]+V[X_3] \\
&+2\mathrm{Cov}[X_1, X_2]+2\mathrm{Cov}[X_2, X_3]+2\mathrm{Cov}[X_1, X_3] )\\
\\
&=\cfrac{1}{9} \times \left(1+1+1+2\times0.5+2\times0.5+2\times0.5 \right)\\
\\
&=\cfrac{1}{9} \times \left(1+1+1+1+1+1 \right)\\
\\
&=\cfrac{1}{9} \times 6\\
\\
&=\cfrac{6}{9}\\
\\
&=\cfrac{2}{3}
\end{align*}
$$
--- 計算終了 ---
分散$${V[Y]=2/3}$$です。

ステップ4:共分散$${\boldsymbol{\mathbf{Cov}[X_1,Y]}}$$の計算
計算途中で公式等を挟みます。
--- 計算開始 ---
$$
\begin{align*}
\mathrm{Cov}[X_1,Y]&=\mathrm{Cov}\left[X_1,\quad \cfrac{1}{3}(X_1+X_2+X_3) \right]\\
\\
&=\mathrm{Cov} \left[ X_1,\quad \cfrac{1}{3}X_1+\cfrac{1}{3}X_2+\cfrac{1}{3}X_3 \right]\\
\end{align*}
$$
--- 計算中断 ---
共分散の分配法則的な公式を用います。
$$
\begin{align*}
&\mathrm{Cov}[aX+bW,\ cY+dZ]\\
&=ac\mathrm{Cov}[X,Y]+ad\mathrm{Cov}[X,Z]+bc\mathrm{Cov}[W,Y]+bd\mathrm{Cov}[W,Z]
\end{align*}
$$
--- 計算再開 ---
$$
\begin{align*}
\mathrm{Cov}[X_1,Y]&=\mathrm{Cov}\left[ X_1,\quad \cfrac{1}{3}X_1+\cfrac{1}{3}X_2+\cfrac{1}{3}X_3 \right]\\
\\
&=\mathrm{Cov}\left[ 1 \cdot X_1,\quad \cfrac{1}{3}X_1+\cfrac{1}{3}X_2+\cfrac{1}{3}X_3 \right]\\
\\
&=\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_1]+\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_2]+\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_3]\\
\end{align*}
$$
--- 計算中断 ---
共分散$${\mathrm{Cov}[X_1,X_1]}$$は分散$${V[X_1]}$$のことなので、値は$${1}$$です。
また、共分散$${\mathrm{Cov}[X_1,X_2],\mathrm{Cov}[X_1,X_3]=0.5}$$でした。
--- 計算再開 ---
$$
\begin{align*}
\mathrm{Cov}[X_1,Y]&=\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_1]+\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_2]+\cfrac{1}{3}\ \mathrm{Cov}[X_1,X_3]\\
\\
&=\cfrac{1}{3} \times 1+\cfrac{1}{3} \times 0.5 + \cfrac{1}{3} \times 0.5\\
\\
&=\cfrac{1}{3} + \cfrac{1}{6} + \cfrac{1}{6}\\
\\
&=\cfrac{1}{3} + \cfrac{2}{6}\\
\\
&=\cfrac{1}{3} + \cfrac{1}{3}\\
\\
&=\cfrac{2}{3}\\
\end{align*}
$$
--- 計算終了 ---
共分散$${\mathrm{Cov}[X_1,Y]=2/3}$$です。
これで役者は全て揃いました。
相関係数$${r[X_1, Y]}$$を計算します。

最終ステップ:相関係数$${\boldsymbol{r[X_1, Y]}}$$の計算
$$
\begin{align*}
r[X_1, Y]&=\cfrac{\mathrm{Cov}[X_1, Y]}{\sqrt{V[X_1]\ V[Y]}}\\
\\
&=\cfrac{2/3}{\sqrt{1\times 2/3}}\\
\\
&=\cfrac{2/3}{\sqrt{2/3}}\\
\\
&=\cfrac{(2/3)^1}{(2/3)^{1/2}}=(2/3)^1 \times (2/3)^{-1/2}=(2/3)^{1/2}=\sqrt{2/3}\\
\\
&=0.8164\cdots
\end{align*}
$$
答えは、$${X_1}$$と$${Y}$$の相関係数$${r[X_1, Y]=0.82}$$です。
お疲れ様でした。

謎のメッセージ
公式問題集の解説最後に記された「確率変数どうしの相関係数よりも、各確率変数の平均との相関係数のほうが高くなる場合がある」・・・。
この謎はいったい・・・、なんの目的で・・・(続く)

解答
⑤ 0.82 です。
難易度 ややむずかしい
・知識:分散・共分散・相関係数の公式
・計算力:数式組み立て(中)、数式計算(中)
・時間目安:3分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は公式問題集で問いかけられた「平均との相関係数が高くなることがある」と言う謎に迫ります。
謎を復唱します
公式問題集の解説の最後に、次のような一文が掲載されています。
[補足]
個別の変数同士の相関係数よりも、各変数の平均との相関係数が高くなることがある。

もう少し噛み砕きます。
【データの素顔】
3つのデータ$${X_1, X_2, X_3}$$があります。
各データはすべて平均$${0}$$、分散$${1}$$です。
また、$${X_1, X_2}$$の相関係数、$${X_2, X_3}$$の相関係数、$${X_1, X_3}$$の相関係数はすべて$${0.5}$$です。
ところで、3つのデータの平均$${Y=(X_1+X_2+X_3)/3}$$があります。
$${X_1, Y}$$の相関係数、$${X_2, Y}$$の相関係数、$${X_3, Y}$$の相関係数はすべて$${\sqrt{2/3} \approx 0.8164}$$です。
【相関係数の謎】
各データ間の相関係数$${0.5}$$よりも、データと平均の相関係数$${0.8164}$$のほうが大きくなっています。
謎は
本当に各データ間の相関係数$${\boldsymbol{0.5}}$$よりも、データと平均の相関係数のほうが大きくなるのか。
データと平均の相関係数は$${\boldsymbol{0.8164}}$$になるのか?
です。
シミュレーションします
では、Pythonでこの謎を実験してみましょう!

①データの概要
3つのデータ$${X_1, X_2, X_3}$$があります。
各データは個数$${n=100}$$で構成され、平均$${\mu=0}$$、分散$${\sigma^2=1}$$です。
$${X_1, X_2}$$の相関係数、$${X_2, X_3}$$の相関係数、$${X_1, X_3}$$の相関係数はすべて$${0.5}$$です。
②確認すること
3つのデータの平均$${Y=(X_1+X_2+X_3)/3}$$と、各データとの間の相関係数、つまり$${r[X_1,Y],\ r[X_2,Y],\ r[X_3,Y]}$$の値はどうなるのでしょうか。
③実施すること
実施の詳細は「Pythonで作成してみよう!」のコーナーで紹介いたします。
・データ$${X_1, X_2, X_3}$$の作成
・相関係数$${r[X_1,Y],\ r[X_2,Y],\ r[X_3,Y]}$$の算出
【作成したデータの概要】

謎を解き明かします
Pythonでこの実験を実行したところ・・・。
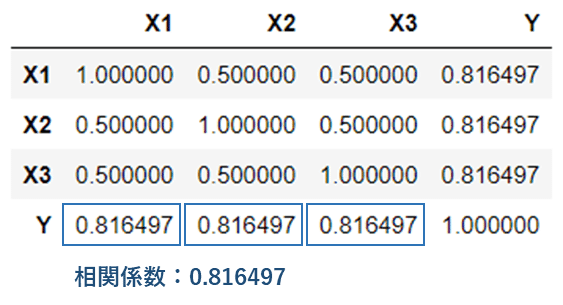
【実験結果】
共分散$${\mathrm{Cov}[X_1,Y],\ \mathrm{Cov}[X_2,Y],\ \mathrm{Cov}[X_3,Y]}$$は、$${0.816497}$$になりました!
各データを散布図行列で可視化します。
横軸と縦軸の交差点に、データ項目ペアの散布図を配置しています。
対角線には、X1, X2, X3, Y(平均) のヒストグラムを配置しています。
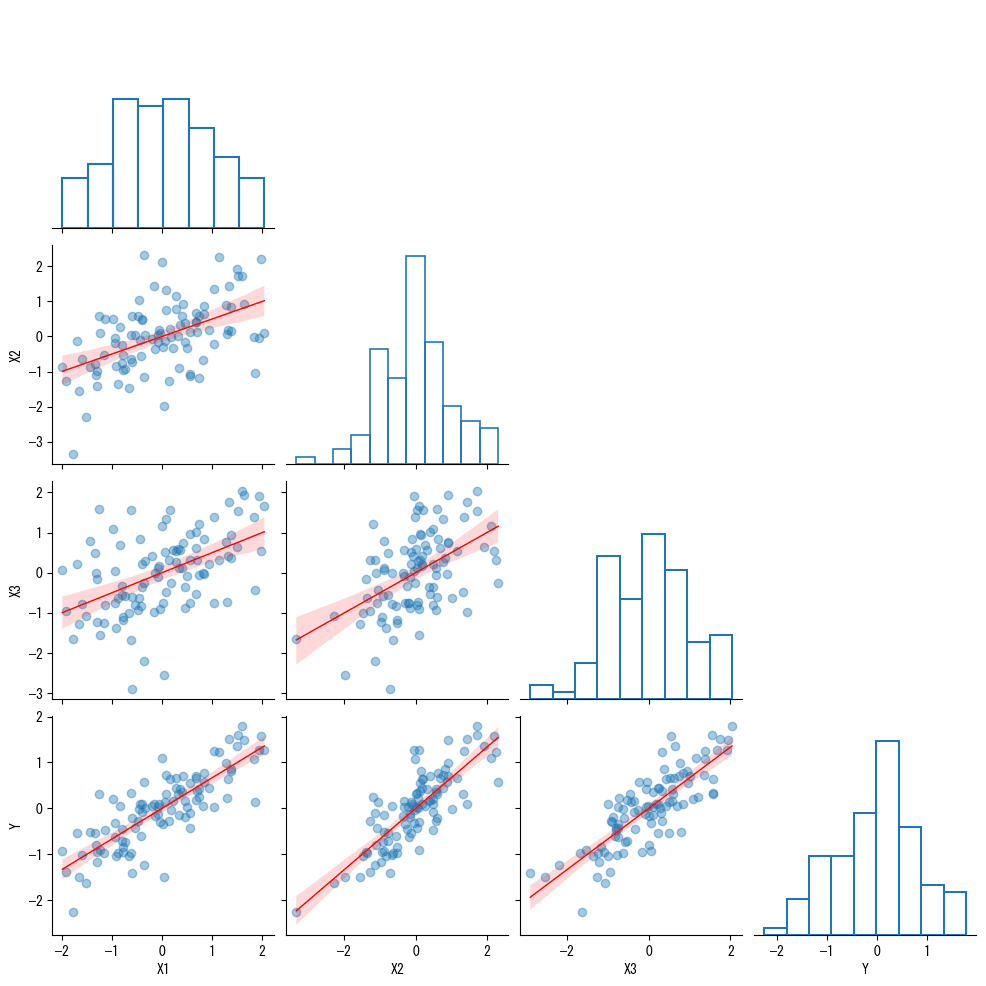
平均 Y と各データの散布図はグラフの一番下の行にあります。
上の散布図と比べて、データの散らばり具合が少ないことがわかります。
散らばり具合が少ないことは、相関係数の値(絶対値)が大きいことを示しています。
公式問題集の解答どおり、各データと平均の間の相関係数$${\boldsymbol{r[X_1,Y],\ r[X_2,Y],\ r[X_3,Y]}}$$の値は大きくなりました!
データシミュレーションのおかげで、数学的に求めた理論的な結論を納得できました。

実践する
シミュレーションを再現してみよう
「知る」の実験を再現してみましょう。
EXCEL、Pythonで実施してみます。
実験用データの共有
CSVファイルのダウンロード
こちらのリンクからCSVファイルをダウンロードできます。
次の「実験用データの作成方法の紹介」の方法で作成しました。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
実験用データの作成方法の紹介
「フリーの統計分析プログラムHAD」(EXCEL)を利用して、実験用データを作成しました。
ありがとうございます!

データの作成方法は次のサイトで紹介されています。
実際のところ、どのようにして乱数を作成するのでしょう?
作成方法を紹介いたします。
1.仮データの作成
①「データ」シートを開きます。
②3つのデータ X1, X2, X3 の列をつくり、数行の仮データを入力します。どんな値でも大丈夫です。
③「データ読み込み」ボタンを押します。

2.使用変数の登録
①「モデリング」シートを開きます。
②「使用変数」ボタンを押します。「分析に使用する変数:HAD」画面が開きます。
③「データリスト」のX1~X3を指定します。
④「追加→」ボタンを押します。右の「使用変数」欄にX1~X3が表示されます。
⑤「OK」ボタンを押します。

3.共分散行列の作成
①「モデリング」シートに戻り、「分析」ボタンを押します。「統計分析マクロ HAD」画面が開きます。
②「共分散行列」チェックボックスにチェックを入れます。
③「OK」ボタンを押します。

4.平均、分散、共分散の設定
①「Cov」シートを開きます。
②図に記載した設定内容にしたがい、データX1~X3の平均、分散、共分散の値を入力します。

5.シミュレーションデータの作成
①「モデリング」シートを開きます。
②「データセット」ボタンを押します。「データセット: HAD」画面が開きます。
③「乱数データ生成」タブの次の値を設定します。
・「シートを指定」:Covと入力します。平均・分散・共分散データを入力したシート名です。
・「サンプルサイズを変更」:100と入力します。データ数を入力します。
・「共分散行列が完全に一致するように生成」:チェックします。
④「OK」ボタンを押します。シミュレーションデータが作成されます。

5.完成したシミュレーションデータの確認
「Random」シートを開きます。
B列~D列にシミュレーションデータが作成されました!
B列=X1、C列=X2、D列=X3として取り扱いましょう。

電卓・手作業で作成してみよう!
今回の実験を手作業で遂行するのは少し厳しいかもしれません。
手作業で実験を再現する場合には、「EXCELで作成してみよう!」「Pythonで作成してみよう!」の内容をお読みいただき、データの平均計算、相関係数計算、散布図の描画作業を実施してください。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
相関係数の計算と散布図の作成
実験用データをEXCELに貼り付けしてから、各行の平均 Y を AVERAGE関数で計算します。

相関係数は CORREL 関数で計算できます。
=CORREL( データ1, データ2 )
次の図の赤枠は X3 と Y の相関係数を計算する例示です。

EXCELの計算結果も、各データ X1, X2, X3 と平均 Y との間の相関係数$${r[X_1,Y],\ r[X_2,Y],\ r[X_3,Y]}$$の値は大きくなりました!

データを散布図で可視化します。
こちらは X1, X2, X3 のデータ間の散布図です。
赤い回帰直線を中心にして見てください。
各点はバラついています。決定係数$${R^2=0.25}$$。

続いて、各データ X1, X2, X3 と平均 Y との間の散布図です。
データの各点は赤い回帰直線に接近しており、バラツキが少なくなっている様子が分かります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、データと平均の間の相関係数が大きくなるかどうかの確認実験に取り組みます。
短いコードで実験できました。
①インポート
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline
pd.options.display.float_format = '{:.6f}'.format②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile)
print(df.shape)
display(df.head())
③データの統計量の確認
まず Pandas の describe() で要約統計量を表示します。
データ個数 100、平均 0、標準偏差=分散 1 であることを確認できました。
df.describe()
続いて、Pandas の corr() で相関係数を表示します。
データ間の相関係数が 0.5 であることを確認できました。
df.corr()
④平均Yの追加
データフレームに平均 Y のカラムを追加します。
df['Y'] = df.mean(axis=1)
print(df.shape)
display(df.head())
⑤平均Yの統計量の確認
平均 Y を含めて、再度、統計量を表示します。
平均 Y の標準偏差が 0.816497 (分散 0.66667)になったことを確認できます。
df.describe()
⑥データX1~X3と平均Yの相関係数の確認
データ X1, X2, X3 と平均 Y の相関係数を表示します。
相関係数は 0.816497 です。
Pythonの計算結果も、各データ X1, X2, X3 と平均 Y との間の相関係数$${r[X_1,Y],\ r[X_2,Y],\ r[X_3,Y]}$$の値は大きくなりました!
df.corr()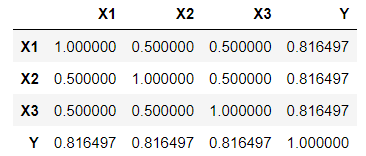
⑦データの可視化
■箱ひげ図
平均 Y のデータ範囲(散らばり具合)が狭まっている様子が分かります。
df.plot.box();
■ペアプロット(散布図行列)
「知る」で紹介した散布図行列です。
sns.pairplot(df, kind='reg', corner=True,
diag_kws=dict(fill=False),
plot_kws=dict(marker='o',
scatter_kws=dict(alpha=0.4),
line_kws=dict(lw=1, color='red')));
■ヒートマップ(相関係数)
相関係数の強さをヒートマップで表現します。
各データ X1, X2, X3 と平均 Y との間の相関係数の色が濃くなっていて、相関係数が大きくなっていることが分かります。
sns.heatmap(df.corr(), cmap='Blues');
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
「数式をごりごり解く楽しさ」と「実データをぐりぐりする楽しさ」の両方を味わえることを目指して、記事を書きました。
いかがだったでしょう?
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
