
「Pythonによる異常検知」を寄り道写経 ~ 第3章3.5節「時系列データにおける異常検知」機械学習編⑥線形回帰
第3章「時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第3章「時系列データにおける異常検知」3.5節「時系列データにおける異常検知」3.5.2項「機械学習による時系列データの異常検知」の通称「寄り道写経」を取り扱います。
7回連続で機械学習を利用した時系列データの異常検知を寄り道写経します!
今回は線形回帰を用いた時系列データの異常検知です。
ではテキストを開いて時系列データの異常検知の旅に出発です🚀
はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
3.5 時系列データにおける異常検知
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
統計解析・機械学習の友、線形回帰で異常検知します。
異常度は観測値と予測値の差の絶対値です。
記事で用いるデータセットはテキスト提供データを引用いたします。
この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
# 機械学習
from sklearn.linear_model import LinearRegression
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')線形回帰を用いた異常検知
テキストによると機械学習の誤差関数からデータ点$${i}$$の異常度$${\alpha_i}$$を定義します。
異常度は、入力データ$${X_i}$$と入力データに対する予測値$${\tilde{h}(X_i;\theta)}$$の差の絶対値です。
入力データ=目的変数の正解値、入力データに対する予測値=目的変数の予測値、と読み替えると以降の機械学習モデルを理解しやすくなります。
データの読み込み
テキストのデータを引用いたします。
ECGデータと呼ばれる心電図の公開データです。期間の単位はミリ秒です。
テキストによると「時系列異常検知のベンチマーク解析に頻繁に用いられる」そうです。
### データの読み込みとデータセットの作成 ※テキストのコードを引用、一部改変
# データの読み込み
data_orgn = pd.read_csv('./data/discord.csv')
# 最初の0~5999件目データを分析
data = data_orgn[:6000]
# 結果表示
print('data.shape:', data.shape)
display(data.head())【実行結果】

STEP 1 データを整える
説明変数になる「ラグ1~3」を作成して、学習データとテストデータに分割します。
機械学習モデルは1~3期前の過去データが説明変数、当期データが目的変数のデータを用いて育てます。
### データの前処理とデータセットの作成 ※テキストのコードを引用、一部改変
# lag1~3を作成
data['lag1'] = data['volume'].shift(1)
data['lag2'] = data['volume'].shift(2)
data['lag3'] = data['volume'].shift(3)
data = data.dropna()
# 学習データとテストデータの分割
point = 2000 # 分割点
X_train = data[['lag1', 'lag2', 'lag3']][:point].values
X_test = data[['lag1', 'lag2', 'lag3']][point:].values
y_train = data['volume'][:point].values
y_test = data['volume'][point:].values
# 結果表示
print('X_train.shape:', X_train.shape)
print('X_test.shape :', X_test.shape)
print('y_train.shape:', y_train.shape)
print('y_test.shape :', y_test.shape)【実行結果】
学習データ 2000、テストデータ 3997 です。

STEP 2 異常度を算出する
通常の機械学習・回帰タスクと同様に、線形回帰のモデルを構築して予測を行います。
観測値と予測値の差を異常度とします。
テキストにあわせて、差の絶対値を異常度にせず、差そのものを異常度にしてます。
最後のプロットでその理由が分かります。
### 線形回帰による予測と異常度算出 ※テキストのコードを引用、一部改変
## 学習と予測
# 線形回帰器の生成
regr = LinearRegression()
# 学習
regr.fit(X_train, y_train)
# 学習データによる予測
y_train_pred = regr.predict(X_train)
# テストデータによる予測
y_test_pred = regr.predict(X_test)
# 予測値の結合
y_pred = np.hstack([y_train_pred, y_test_pred])
## 異常度の算出
# (観測値-予測値)の絶対値、にしたいけれども描画の都合で変更
train_anomaly = y_train_pred - y_train
test_anomaly = y_test_pred - y_test
anomaly_score = np.hstack([train_anomaly, test_anomaly])
# 結果表示
print('train_anomaly.shape:', train_anomaly.shape)
print(train_anomaly[:5], '...')
print('\ntest_anomaly.shape :', test_anomaly.shape)
print(test_anomaly[:5], '...')【実行結果】

STEP 3 異常度の閾値を算出する
なんとなく分位点法を使ってみます。
テキストは異常度の閾値に言及しておらず、テキストオリジナルコードでは 21 番目に大きい異常度を閾値にしています。
分位点を$${0.35\%}$$とすることで、21 番目に大きい異常度が閾値になります。
### 異常度の閾値の算出 by 分位点法
# 分位%点の設定
q = 0.0035
# 閾値の算出
num_quantile = int(round(len(anomaly_score) * q, 0))
threshold = sorted(abs(anomaly_score))[::-1][num_quantile - 1]
# 閾値の表示
print('分位点数:', num_quantile)
print('閾値:', threshold)【実行結果】
異常度の閾値はおよそ 0.37 です。
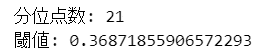
STEP 4 異常値を確認する
異常値を可視化します。
可視化関数を定義します。
### 機械学習による異常検知のテスト結果の描画関数の定義
def plot_anomaly(data, train_anomaly, test_anomaly, threshold, title='機械学習'):
# 描画領域の設定 gs:gridspecで上下のaxesの高さを5:2にする
fig = plt.figure(figsize=(10, 5))
gs = fig.add_gridspec(2, 1, height_ratios=(5, 2))
ax1 = fig.add_subplot(gs[0, 0])
ax2 = fig.add_subplot(gs[1, 0])
## 上段の描画
# 観測値の描画
ax1.plot(data, color='tab:blue', lw=0.9)
# 修飾
ax1.set(ylabel="ECG's value[$ms^2/Hz$]")
ax1.grid(lw=0.5)
## 下段の描画
# 学習データの異常度の描画
ax2.plot(train_anomaly, color='coral', lw=0.9)
# テストデータの異常度の描画
ax2.plot(range(len(train_anomaly), len(data)),
test_anomaly, color='tab:red', lw=0.9)
# 閾値の水平線の描画
ax2.hlines(threshold, 0, 6000, color='red', ls='--')
# 修飾
ax2.sharex(ax1)
ax2.set(ylabel='異常度')
ax2.grid(lw=0.5)
# 全体修飾
fig.suptitle(f'{title}よる異常検知\n'
f'上段:観測値、下段:異常度 閾値{threshold:.3f}')
fig.supxlabel('時間[ミリ秒]')
plt.tight_layout()
plt.show()可視化の実行です。
テキストの図3.49 (c) に相当するグラフを描画します。
### 異常度の可視化 ★図3.49(c)に相当
plot_anomaly(data, train_anomaly, test_anomaly, threshold, 'Linear Regression')【実行結果】
上段の青い線が観測値です。
観測値は4300ミリ秒あたりに他の時間と異なる部位があります。
下段では異常度を描画しています。
オレンジの線が学習データの異常度、赤い線がテストデータの異常度です。

テキストは見事に異常部位を検知していますが、私のコードは検知がうまくいっていないようです…残念…
閾値を超える正値の大きな誤差は1000ミリ秒あたりを始め6個ほどあります。
一方で4300ミリ秒あたりの異常部位の異常度は閾値に達していません。
テキストの図 3.49 (e) に相当する「予測結果と実測値を同時にプロット」する図を描画します。
### 予測結果と実測値を同時にプロット ★図3.49(e)に相当
# ※テキストのコードを引用、一部改変
# x軸の値の設定
xticks = range(3800, 4800)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(10, 3))
# 観測値の描画
ax.plot(xticks, data.values[3800:4800, 0], color='tab:blue', lw=0.8,
label='観測値')
# 予測値の描画
ax.plot(xticks, y_pred[3800:4800], color='tab:red', lw=0.8, ls='--',
label='予測値')
# 修飾
ax.set(xlabel='時間 [ミリ秒]', ylabel="ECG's value [$ms^2/Hz$]",
title='観測値・予測値同時プロット')
ax.legend()
ax.grid(lw=0.5);【実行結果】

4300ミリ秒あたりの観測値の下振れ部分に対して、予測値も追随して異常な動きを捉えてしまっています!
予測値が異常部位を捉えてしまい、観測値と予測値の差(誤差)が小さくなったことが、上の図で異常検知できなかった理由と考えられます。
テキストがどうやって線形回帰で異常検知できたのか、知りたいです。
大きな疑問が残ってしまいました…
今回の寄り道写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
