
「回帰分析から学ぶ計量経済学」をPythonで写経 ~ 第1章「データを関連づける」①データの分析と可視化
第1章「データを関連づける」
書籍の著者 山澤成康 先生
この記事は、書籍「回帰分析から学ぶ計量経済学」第1章「データを関連づける」の Python写経活動 を取り扱います。
今回は 1変数・2変数の代表値と可視化 に取り組みます!
では書籍を開いて回帰分析の旅に出発です🚀

はじめに
書籍「回帰分析から学ぶ計量経済学」のご紹介
このシリーズは書籍「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」(オーム社、「テキスト」と呼びます)の Python 写経です。
テキストは、2023年11月に発売され、副題「Excelで読み解く経済のしくみ」のとおり、主に Excel を用いて、計量経済学を平易に学べる素晴らしい書籍です。
テキストの「はじめに」に著者の先生が執筆の動機を書かれています。
社会人の統計リテラシーの向上をテーマの1つとした科研費プロジェクトの最終年度で、広く社会人に向けてわかりやすい経済分析の本を書きたかったのです。
私にとって計量経済学は高嶺の花ですが、このテキストでさまざまな回帰分析のアプローチを知ることができました。
また、書籍の Excel 処理を Python に置き換える「寄り道写経」の実践を通じて、回帰分析のお気持ちに少し近づけた感じがいたします。
回帰分析に慣れ親しむのに丁度良いレベル感と内容ですので、これはぜひともブログにしたい!と思って現在に至ります。
計量経済学の色を薄め、データ分析の色を濃いめに書いてまいります!

引用表記
この記事は、出典に記載の書籍に掲載された文章と配布データを引用し、適宜、掲載文章・配布データを改変して書いています。
【出典】
「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」
第1版第1刷、著者 山澤成康、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
第1章 データを関連づける
この記事は第1章の以下の節を取り扱います。
Talk この章のマホナたちの会話
1.1 統計データとは
1.2 1つのデータの分析
1.3 2つのデータの分析
1.4 実質GDPと鉱工業生産の例
記事に用いるデータは、オーム社の書籍紹介サイトからダウンロードできる Excel ファイル内のデータをもとにしてCSVファイルを作成し、data フォルダに格納しています。
第1章で用いるライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 機械学習(線形回帰・OLS)
from sklearn.linear_model import LinearRegression
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
Talk マホナたちの会話
テキストの各章の冒頭で繰り広げられるキャラクターたちのトークでは、章で学ぶテーマをダイジェストで紹介しています。
■ リンゴの木のヒストグラム p.19
テキストは、1変数のデータを把握できるグラフの一例としてヒストグラムを紹介しています。
リンゴデータを読み込みます。
### データの読み込み
df1 = pd.read_csv('./data/01_01_apple_tree.csv')
print('df1.shape:', df1.shape)
display(df1.head())【実行結果】
100年間のリンゴの木の本数と収穫量のデータです。
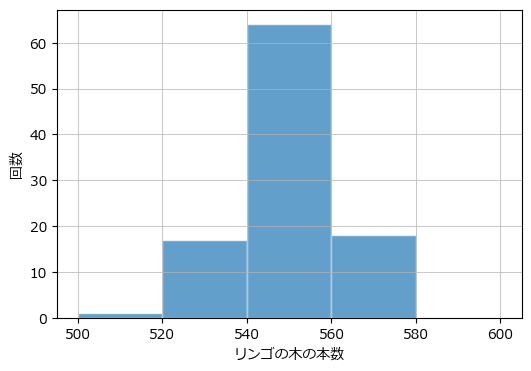
ヒストグラムを描画します。
こちらは matplotlib ライブラリを利用しています。
### リンゴの木の本数のヒストグラムの描画 by matplotlib
# 描画領域の設定
plt.figure(figsize=(6, 4))
# ヒストグラムの描画
plt.hist(df1['リンゴの木'], bins=range(500, 601, 20), ec='white', alpha=0.7)
# 修飾
plt.xlabel('リンゴの木の本数')
plt.ylabel('回数')
plt.grid(lw=0.5)
plt.show()【実行結果】
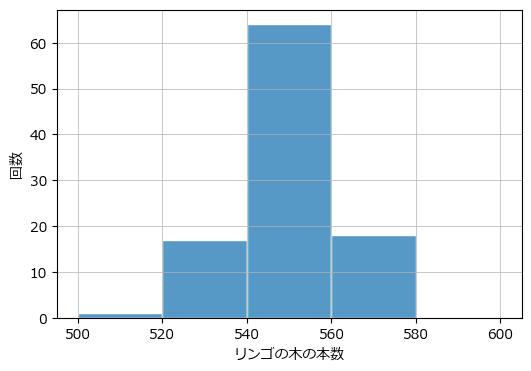
続いて seaborn ライブラリで描画します。
### リンゴの木の本数のヒストグラムの描画 by seaborn
# 描画領域の設定
plt.figure(figsize=(6, 4))
# ヒストグラムの描画
sns.histplot(data=df1, bins=range(500, 601, 20), x='リンゴの木', ec='white')
# 修飾
plt.xlabel('リンゴの木の本数')
plt.ylabel('回数')
plt.grid(lw=0.5)
plt.show()【実行結果】
■ リンゴの木の数とリンゴの収穫量の散布図 p.21
テキストは、2変数のデータの関係を把握できるグラフの一例として散布図を紹介しています。
先程読み込んだリンゴデータを利用して散布図を描画します。
こちらは matplotlib ライブラリを利用しています。
### リンゴの木の本数とリンゴの収穫量の散布図の描画 by matplotlib
# 描画領域の設定
plt.figure(figsize=(6, 4))
# ヒストグラムの描画
plt.scatter(df1['リンゴの木'], df1['リンゴの収穫量'], ec='white', alpha=0.8)
# 修飾
plt.xlabel('リンゴの木の数')
plt.ylabel('リンゴの収穫量')
plt.grid(lw=0.5)
plt.show()【実行結果】
正の相関関係が見られます。
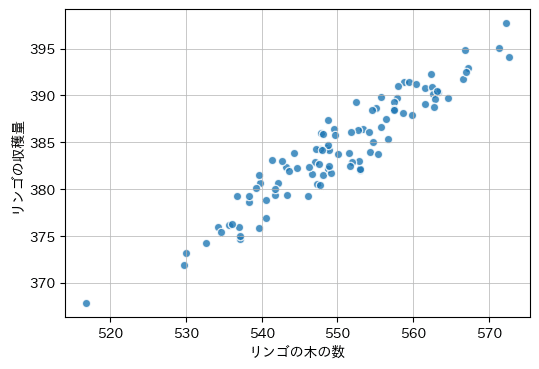
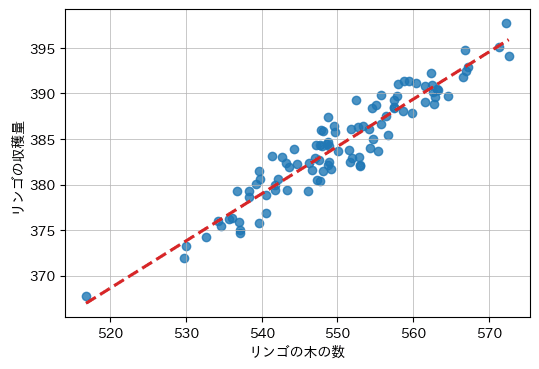
続いて seaborn の regplot で散布図と回帰直線を描画します。
### リンゴの木の本数とリンゴの収穫量の散布図の描画 by seaborn
# 描画領域の設定
plt.figure(figsize=(6, 4))
# ヒストグラム+回帰直線の描画
sns.regplot(data=df1, x='リンゴの木', y='リンゴの収穫量', ci=None,
line_kws={'color': 'tab:red', 'ls': '--'})
# 修飾
plt.xlabel('リンゴの木の数')
plt.ylabel('リンゴの収穫量')
plt.grid(lw=0.5)
plt.show()【実行結果】
このグラフではテキストのような回帰式と決定係数を表示していません。
■ 決定係数=0.99 p.27
決定係数 0.99 のデータを読み込んで、実際に決定係数を計算し、散布図を描画します。
まずはデータを読み込みます。
### データの読み込み
df2 = pd.read_csv('./data/01_02_R2.csv')
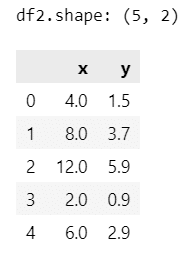
print('df2.shape:', df2.shape)
display(df2)【実行結果】
とてもシンプルなデータです。
回帰分析を実行して、決定係数を求めます。
scikit-learn の LinearRegression クラスを利用します。
### 回帰分析の実行と決定係数の算出
# 説明変数Xと目的変数yの作成
X = df2.x.values.reshape(-1, 1)
y = df2.y
# 回帰分析の実行
reg = LinearRegression().fit(X, y)
# 回帰直線の取得
x_pred = np.array([X.min(), X.max()]).reshape(-1, 1)
y_pred = reg.predict(x_pred)
# 決定係数の取得
R2 = reg.score(X, y)
print('R² = ', R2)【実行結果】
決定係数は約 0.99 です!
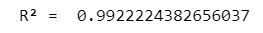
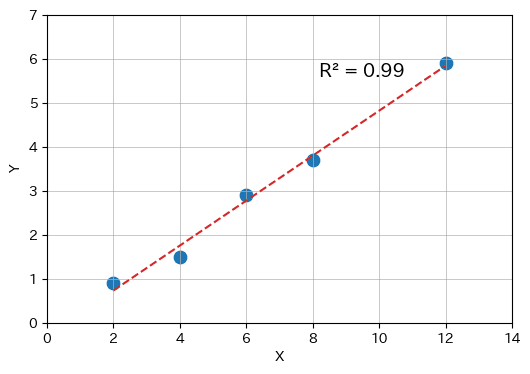
散布図と回帰直線を描画します。
### 散布図と回帰直線の描画
# 描画領域の設定
plt.figure(figsize=(6, 4))
# 散布図の描画
plt.scatter(df2.x, df2.y, s=80)
# 回帰直線の描画
plt.plot(x_pred, y_pred, color='tab:red', ls='--')
# 決定係数の表示
plt.text(x=8.2, y=5.6, s=f'R² = {R2:.2f}', fontsize=14)
# 修飾
plt.xlim(0, 14); plt.ylim(0, 7)
plt.xlabel('X'); plt.ylabel('Y')
plt.grid(lw=0.5)
plt.show()【実行結果】
テキストのようなチャートを描画できました。

1.2 1つのデータの分析
■ 経済学のヒストグラム p.30
あらためてヒストグラムを描画します。
経済学得点データを読み込みます。
### データの読み込み
df3 = pd.read_csv('./data/01_03_ecomony_score.csv')
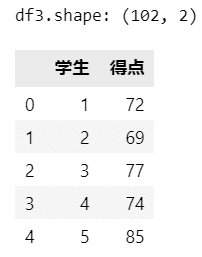
print('df3.shape:', df3.shape)
display(df3.head())【実行結果】
テキストには学生 100 人のデータと記載されていますが、Excelデータには 102 人分がセットされています。
ヒストグラムを matplotlib で描画します。
### ヒストグラムの描画 by matplotlib
# 描画領域の設定
plt.figure(figsize=(6, 4))
# ヒストグラムの描画
plt.hist(df3['得点'], bins=range(40, 101, 10), ec='white', alpha=0.7)
# 修飾
plt.xlabel('得点')
plt.ylabel('頻度 [人]')
plt.grid(lw=0.5)
plt.show()【実行結果】
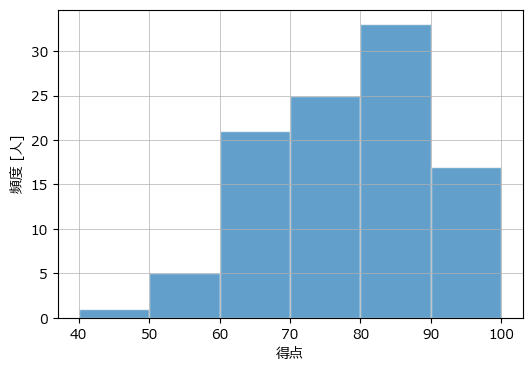
テキストのヒストグラムと異なる形状です。
この図の階級の区間は 40以上50未満、50以上60未満のように、左側が閉区間、右側が開区間になっています。
テキストの区間は40超50以下、50超60以下のように左側が開区間、右側が閉区間になっています。
■ 代表値 p.31
経済学得点データを用いて、テキスト p32 の代表値を算出してみます。
1変数データなので相関係数は算出しません。
最初に pandas の describe() で代表値の一部を算出します。
### 要約統計量の表示 ※分散・標準偏差は不偏分散にもとづく
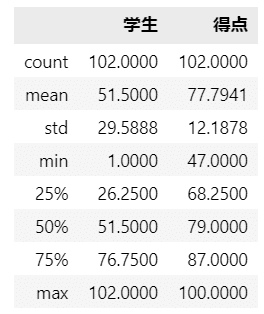
display(df3.describe().round(4))【実行結果】
上からデータの個数、平均値、標準偏差、最小値、第一四分位数、中央値、第三四分位数、最大値です。
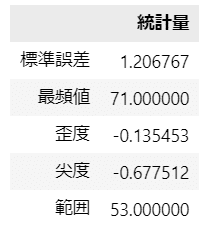
続いて、describe() で算出できない代表値を算出します。
### その他の統計量
# 標本サイズ
N = df3.shape[0]
# 標準誤差
std_err_val = df3['得点'].std() / np.sqrt(N)
# 最頻値
mode_val = df3['得点'].mode()[0]
# 歪度
skew_val = df3['得点'].skew()
# 尖度
kurt_val = df3['得点'].kurt()
# 範囲
range_val = df3['得点'].max() - df3['得点'].min()
# データフレーム化
stats_df3 = pd.DataFrame(
[std_err_val, mode_val, skew_val, kurt_val, range_val],
index=['標準誤差', '最頻値', '歪度', '尖度', '範囲'],
columns=['統計量']
)
display(stats_df3)【実行結果】

1.3 2つのデータの分析
■ 散布図 p.33
あらためて散布図を描画します。
数学と英語の得点データを読み込みます。
### データの読み込み
df4 = pd.read_csv('./data/01_04_scores.csv')
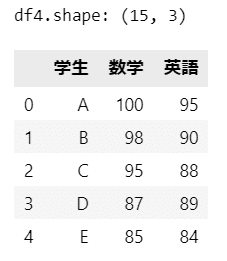
print('df4.shape:', df4.shape)
display(df4.head())【実行結果】
15人の得点データです。
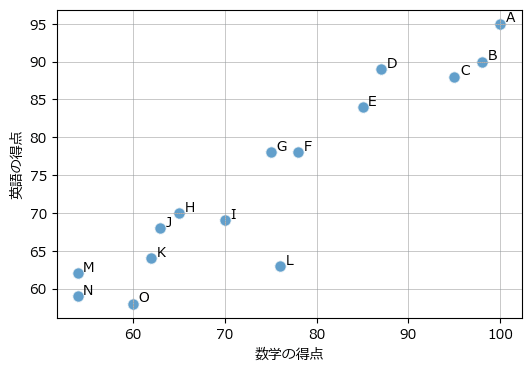
散布図を matplotlib で描画します。
### 散布図の描画 by matplotlib
# 描画領域の設定
plt.figure(figsize=(6, 4))
# 散布図の描画
plt.scatter(df4['数学'], df4['英語'], s=70, ec='white', alpha=0.7)
# 学生の表示
for i in range(len(df4)):
plt.text(x=df4.iloc[i, 1]+0.6, y=df4.iloc[i, 2]+0.2, s=df4.iloc[i, 0])
# 修飾
plt.xlabel('数学の得点')
plt.ylabel('英語の得点')
plt.grid(lw=0.5)
plt.show()【実行結果】
データ点の脇の文字は学生を示す記号です。
■ 相関係数 p.34
相関係数が異なるデータの散布図を描画します。
数学と英語の得点データを読み込みます。
### データの読み込み
df5 = pd.read_csv('./data/01_05_corr.csv')
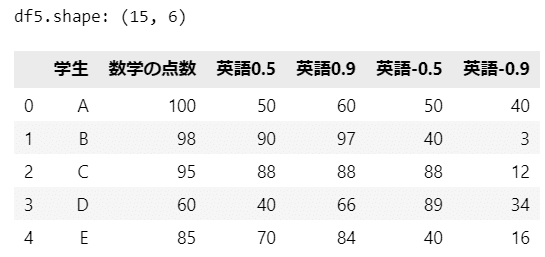
print('df5.shape:', df5.shape)
display(df5.head())【実行結果】
15人のデータです。
英語の得点が相関係数$${0.5, 0.9, -0.5, -0.9}$$のパターンごとに格納されています。
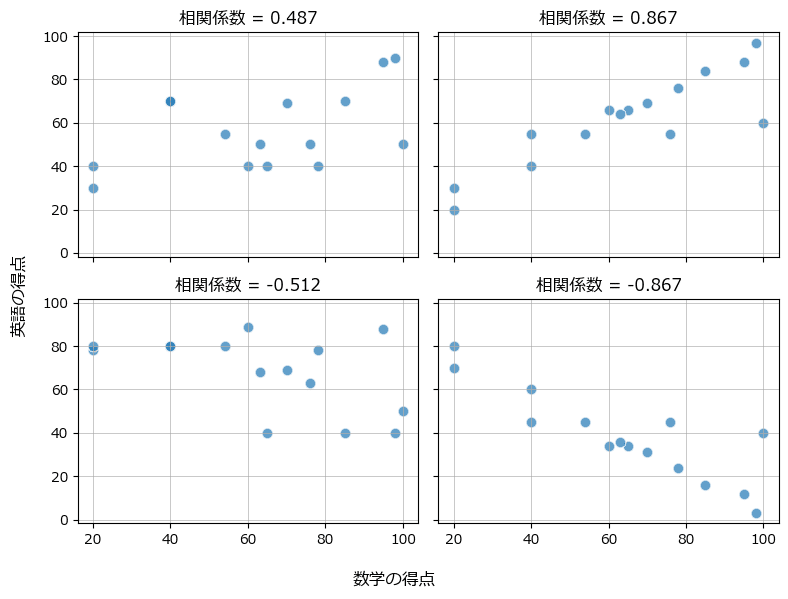
4パターンの散布図を matplotlib で描画します。
相関係数を付記します。
### 散布図の描画 by matplotlib
# 描画領域の設定
fig, axes = plt.subplots(2, 2, figsize=(8, 6), sharex=True, sharey=True)
# 4つの英語の得点ごとに散布図描画を繰り返し処理
for col, ax in zip(df5.columns[2:], axes.flat):
# 散布図の描画
ax.scatter(df5['数学の点数'], df5[col], s=60, ec='white', alpha=0.7)
# 修飾
ax.set(title=f"相関係数 = {df5[['数学の点数', col]].corr().values[0, 1]:.3f}")
ax.grid(lw=0.5)
# 全体修飾
fig.supxlabel('数学の得点')
fig.supylabel('英語の得点')
plt.tight_layout()
plt.show()【実行結果】
相関係数の絶対値が大きい右側の散布図は、データ点が直線的に並んでいます。

1.4 実質GDPと鉱工業生産の例
■ 実質GDPと鉱工業生産指数の折れ線グラフ p.35
実質GDPと鉱工業生産指数について、①データ値、②前期比伸び率の2つのチャートを折れ線グラフで描画します。
データを読み込んで、描画用の前処理を行います。
### データの読み込み
# csvファイルの読み込み
df6 = pd.read_csv('./data/01_06_gdp_iip.csv', index_col=0, usecols=[0, 1, 2])
# 四半期日付インデックスの作成
df6.index = pd.date_range(start='1994-03-31', periods=df6.shape[0], freq='QE')
# 前期比伸び率列を追加
df6['GDP前期比伸び率'] = df6['GDP'].pct_change() * 100
df6['IIP前期比伸び率'] = df6['IIP'].pct_change() * 100
# データフレームの表示
print('df6.shape:', df6.shape)
display(df6)【実行結果】
1994年3月期から2023年3月期までの117四半期のデータです。
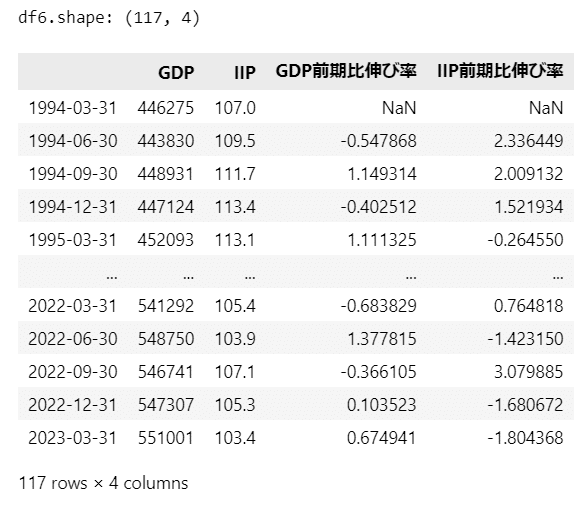
続いて2つの折れ線グラフを描画します。
#### 実質GDPと鉱工業生産指数の動きの描画
## 設定と準備
cols = [['GDP', 'IIP'], ['GDP前期比伸び率', 'IIP前期比伸び率']] # 変数
ylabels = [['実質GDP [10億円]', '鉱工業生産指数 [2020年=100]'], # y軸ラベル
['実質GDP伸び率 [%]', '鉱工業生産指数伸び率 [%]']]
ylims = [[(0, 600000), (0, 140)], [(-10, 8), (-25, 10)]] # y軸の範囲
titles = ['実質GDPと鉱工業生産指数', # グラフタイトル
'実質GDPと鉱工業生産指数(前期比伸び率)']
## 描画領域の設定
fig, ax = plt.subplots(1, 2, figsize=(12, 4))
## 左右の2つのグラフごとにGDPとIIPの描画を繰り返し処理
for i in range(2):
## GDP
# GDPの折れ線グラフの描画
ax[i].plot(df6[cols[i][0]], label='実質GDP')
# 修飾
ax[i].set(ylim=ylims[i][0], xlabel='日付 [四半期]', ylabel=ylabels[i][0],
title=titles[i])
ax[i].grid(lw=0.5)
## 鉱工業生産指数
# 右軸のaxesを作成 ※twinx()・・・1つグラフにy軸が異なる2つのグラフ描画が可能
ax_twin = ax[i].twinx()
# 鉱工業生産指数の折れ線グラフの描画
ax_twin.plot(df6[cols[i][1]], color='tab:red', label='鉱工業生産指数')
# 修飾
ax_twin.set(ylim=ylims[i][1], ylabel=ylabels[i][1])
# 2つのaxesの凡例を1つにまとめて表示
# http://taustation.com/axes-twinx-dual-y-axes/
handles, labels = ax[i].get_legend_handles_labels()
handles_twin, labels_twin = ax_twin.get_legend_handles_labels()
ax[i].legend(handles=handles + handles_twin, labels=labels + labels_twin,
loc='lower left')
## 全体調整
plt.tight_layout()
plt.show()【実行結果】
実質GDPと鉱工業生産指数は単位が異なるので、縦軸を左右で変更できる twinx() を利用しました。
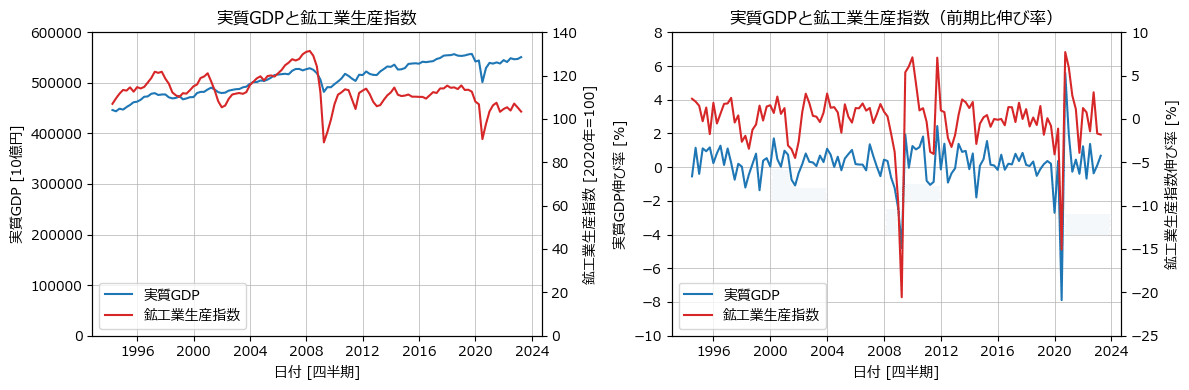
■ 実質GDPと鉱工業生産指数のヒストグラム p.36
実質GDPと鉱工業生産指数のバラツキの違い可視化する目的で、前期比伸び率のヒストグラムを描画します。
### ヒストグラムの描画
# ビンの設定
bins = range(-23, 10, 1)
# 描画領域の設定
plt.figure(figsize=(6, 4))
# 実質GDPのヒストグラムの描画
plt.hist(df6['GDP前期比伸び率'], bins=bins, color='lightblue', ec='tab:blue',
alpha=0.5, label='実質GDP')
# 鉱工業生産指数のヒストグラムの描画
plt.hist(df6['IIP前期比伸び率'], bins=bins, color='tab:red', histtype='step',
label='鉱工業生産指数')
# 修飾
plt.xlabel('実質GDP, 鉱工業生産指数の前期比伸び率 [%]')
plt.ylabel('頻度 [四半期]')
plt.legend()
plt.grid(lw=0.5)
plt.show()【実行結果】
テキストのとおり、鉱工業生産指数の方がバラツキが大きく、実質GDPの方が尖り具合が大きく、両方とも右に偏ったデータであることが分かりました。
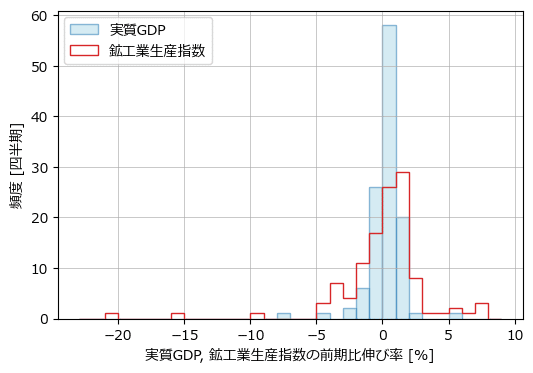
基本統計量を確認します。
基本統計量算出関数を定義します。
### 基本統計量算出関数の定義
def calc_stats(x): # x: pandas.Series
# 設定と準備
x = x.dropna() # 1行目のNaNを削除
result = [] # 結果を格納するリストの初期化
N = len(x) # 標本サイズ
# 統計量の算出
result.append(x.mean()) # 平均値
result.append(x.std(ddof=1) / np.sqrt(N)) # 標準誤差
result.append(x.median()) # 中央値
result.append(x.mode()[0]) # 最頻値
result.append(x.std(ddof=1)) # 標準偏差
result.append(x.var(ddof=1)) # 分散
result.append(x.kurt()) # 尖度
result.append(x.skew()) # 歪度
result.append(x.max() - x.min()) # 範囲
result.append(x.min()) # 最小
result.append(x.max()) # 最大
result.append(x.sum()) # 合計
result.append(N) # データの個数
# ラベルの設定
labels = ['平均値', '標準誤差', '中央値', '最頻値', '標準偏差', '分散',
'尖度', '歪度', '範囲', '最小', '最大', '合計', 'データの個数']
return result, labels実質GDPと鉱工業生産指数の前期比伸び率の基本統計量を算出します。
### 基本統計量の算出
stats_df6 = pd.DataFrame(
{'GDP': calc_stats(df6['GDP前期比伸び率'])[0],
'鉱工業生産指数': calc_stats(df6['IIP前期比伸び率'])[0]},
index=calc_stats(df6['GDP前期比伸び率'])[1],
)
display(stats_df6.round(2))【実行結果】
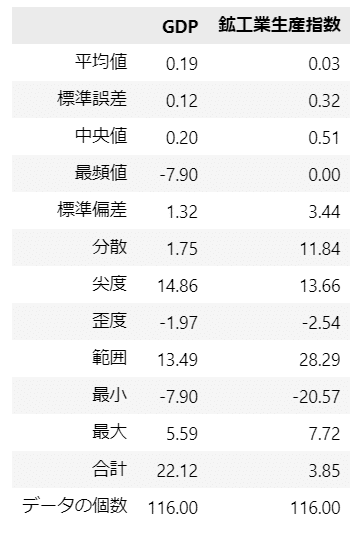
テキストのとおり
・バラツキ:標準偏差は鉱工業生産指数の方が大きい
・尖り具合:尖度は実質GDPの方が大きい
・左右の偏り:歪度は両者ともマイナスであり、右側に偏っている
今回の写経は以上です。
シリーズの記事
次の記事
前の記事

目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
