10-1-3 出力結果の解釈・残差・信頼区間 ～ R の回帰分析出力結果を徹底的に洗います
今回の統計トピック
回帰分析テーマの３回目です。
R の回帰分析の出力結果を細かく見ていきましょう！
今回はデータを用意できなかったので、座学中心となります。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！
問題を解く
📘公式問題集のカテゴリ
線形モデルの分野 ～回帰分析の分野
問3 出力結果の解釈・残差・信頼区間（クレアチニンと糸球体濾過量）
試験実施年月
調査中
問題
公式問題集をご参照ください。
解き方
題意
統計ソフトウェアの出力結果から次の３問を解答します。
① 決定係数・自由度調整済み決定係数・回帰係数・残差・検定統計量
② 適切な残差プロットの選択
③ 回帰係数の90%信頼区間の計算
【条件】
・標本サイズ197の観測データより、糸球体濾過量（GFR）とクレアチニン（Cre）の値を用いて、統計ソフトウェアを使って線形単回帰を実施
・統計ソフトウェアの出力結果は下の図を参照
・散布図の表示は省略（公式問題集をご参照ください）
【統計ソフトウェアの出力結果イメージ】
■ 回帰式
ひとまず、回帰式を書きましょう。
$${\text{GFR}=121.052 -60.263 \times \text{Cre}}$$
回帰式をもとにして回帰直線を描画しましょう。
回帰式のイメージを膨らませましょう！
問１ 出力結果から読み取れる情報のうち正しいものを選択
文章①
決定係数 0.4888 と 自由度調整済み決定係数 0.4861 の差は回帰モデルの自由度か？
決定係数と自由度調整済み決定係数は次の箇所に記載されています。
ところで、決定係数と自由度調整済み決定係数は、モデルの当てはまり具合を把握できる指標です。
決定係数は、総平方和に占める回帰による平方和の割合です。
$$
\begin{align*}
R^2&=\cfrac{S_R}{S_T}=1-\cfrac{S_e}{S_T} \\
\\
決定係数&=\cfrac{回帰による平方和}{総平方和}=1-\cfrac{残差平方和}{総平方和} \\
\\
\end{align*}
$$
自由度調整済み決定係数は、説明変数の数が異なるモデル間の比較に活用できる指標です。
$$
R^{*2} = 1 - \cfrac{S_e/(n-p-1)}{S_T/(n-1)}
$$
２つの式を差し引きしても、自由度を求めることはできません。
なお、自由度に関しては、残差平方和の自由度は$${n-p-1=197-1-1=195}$$、総平方和の自由度は$${n-1=197-1=196}$$です。
残差の自由度は統計ソフトウェアの出力結果に表示されています。
文章①は適切ではありません。
文章②
決定係数・自由度調整済み決定係数は0.5以下なので、回帰式を用いた GFR の予測値は 50%以上の確率で誤りか？
決定係数・自由度調整済み決定係数は、回帰による平方和と全平方和の割合を基礎とした「モデルの当てはまり具合」を示す指標です。
モデルの予測値の正解率を示すものではありません。
文章②は適切ではありません。
文章③
説明変数と目的変数を入れ替えて回帰分析を行うと、説明変数（元・目的変数）の回帰係数の推定値は、入れ替える前の回帰係数の逆数$${1/-60.263}$$か？
説明変数の回帰係数の表示を確認しましょう。
続いて、最小二乗法による単回帰の傾き$${\hat{\beta}}$$の公式を確認しましょう。
$$
\hat{\beta}=\cfrac{\sum^n_{i=1}(y_i-\bar{y})(x_i-\bar{x})}{\sum^n_{i=1}(x_i-\bar{x})^2}=\cfrac{T_{xy}}{T_{xx}}=\cfrac{\hat{\sigma}_{xy}}{\hat{\sigma}^2_x}=r_{xy}\cfrac{\hat{\sigma}_y}{\hat{\sigma}_x}
$$
$${\cfrac{\hat{\sigma}_{xy}}{\hat{\sigma}^2_x}}$$に注目しましょう。
分母は説明変数の不偏分散$${\hat{\sigma}^2_x}$$です。
この式の目的変数$${y}$$と説明変数$${x}$$を入れ替えてみます。
$${\cfrac{\hat{\sigma}_{xy}}{\hat{\sigma}^2_y}}$$です。
分母が目的変数の不偏分散$${\hat{\sigma}^2_y}$$に変わりました。
$${\hat{\sigma}^2_x=\hat{\sigma}^2_y}$$のとき、目的変数と説明変数を入れ替えて、回帰係数が逆数になるのです。
では、説明変数 Cre と目的変数 GFR の不偏分散は等しいのでしょうか？
散布図の値の単位を確認します。
説明変数 Cre は 0.2 ～ 1.7 の範囲の点です。
目的変数 GFR は 20 ～ 140 の範囲の点です。
両者のスケールに大きな差があるので、不偏分散には差があると想定されます。
不偏分散が等しくないので、回帰係数は逆数にならないと言えます。
文章③は適切ではありません。
文章④
残差の平均は残差の中央値 -0.816 より大きいか？
残差の中央値の表示を確認しましょう。
突然ですが「回帰の主な性質」の降臨です。
「最小二乗法による回帰係数を用いる場合の回帰式の性質 ｂ」をご存知でしょうか？
『ｂ．残差$${\boldsymbol{e_i=y_i-\hat{y}}}$$の平均は０である』です。
$${残差の中央値 -0.816 < 残差の平均 0}$$の関係が明らかになりました。
残差の平均は残差の中央値 -0.816 より大きいです。
文章④は適切です。
文章⑤
切片と傾きの推定値の有意性は「F-statistic」の値で判断できるか？
切片と傾きの推定値の表示を確認しましょう。
切片と傾きの推定値の検定は、$${t}$$検定統計量を用いた$${t}$$検定です。
上の図の「t value」が検定統計量の値$${t}$$値です。
その隣の「Pr(>|t|)」が$${t}$$値に対する$${p}$$値であり、この$${p}$$値で有意性の判断をします。
切片と傾きの$${p}$$値は$${1\%}$$未満なので、有意水準$${1\%}$$で有意であり、「切片と傾きの値は０では無い」と言えます。
ちなみに、「F-statistic」、すなわち$${F}$$値は次の箇所に表示されています。
$${F}$$値は「回帰の有意性の検定」の検定統計量です。
$${F}$$値に対する$${p}$$値「p_value」は$${1\%}$$未満です。
有意水準$${1\%}$$で「回帰係数のうち少なくとも１つは０では無い」と言えます。
文章⑤は適切ではありません。
問１の解答は ④ です。
問２ 問題に記載されている４つの残差プロットから適切なものを１つ選ぶ
この残差プロットは横軸「説明変数」、縦軸「残差」です。
「統計ソフトウェアの出力結果」の「残差」の表示を確認しましょう。
残差の最小値・最大値・四分位数が表示されています。
この最小値$${-33.650}$$と最大値$${44.298}$$が当てはまる残差プロットを探しましょう。
各残差プロットの縦軸の最小値と最大値を確認します。
①：最小値$${-35}$$、最大値$${50}$$弱
②：最小値$${-40}$$、最大値$${60}$$弱
③：最小値$${-40}$$、最大値$${40}$$
④：最小値$${-20}$$、最大値$${60}$$弱
① が最も残差の最小値・最大値に近いです。
問２の解答は ① です。
問３ Cre の回帰係数（傾き）の 90% 信頼区間を計算する
まず傾きの信頼区間の公式を確認しましょう。
$$
\hat{\beta} \pm t_{\alpha/2}(n-p-1)\sqrt{\cfrac{\hat{\sigma}^2}{T_{xx}}}
$$
日本語にすると次のようになります。
傾きの推定値 ± 自由度$${(n-p-1)}$$の$${t}$$分布の上側$${\alpha/2 \%}$$点 × 傾きの推定値の標準誤差
統計ソフトウェアの出力結果から、傾きの推定値、傾きの推定値の標準誤差を取得できます。
傾きの推定値は$${-60.263}$$、傾きの推定値の標準誤差は$${4.414}$$です。
続いて、自由度$${(n-p-1)}$$の$${t}$$分布の上側$${\alpha/2 \%}$$点を検討しましょう。
$${90\%}$$信頼区間なので、$${\alpha=1-0.9=0.1}$$であり、$${\alpha/2=0.1/2=0.05=5\%}$$です。
また自由度は、標本サイズ$${n=197}$$、説明変数の数$${p=1}$$ですので、$${n-p-1=197-1-1=195}$$です。
では$${t}$$分布のパーセント点表より、自由度$${195}$$の$${t}$$分布の上側$${5\%}$$点を取得しましょう。
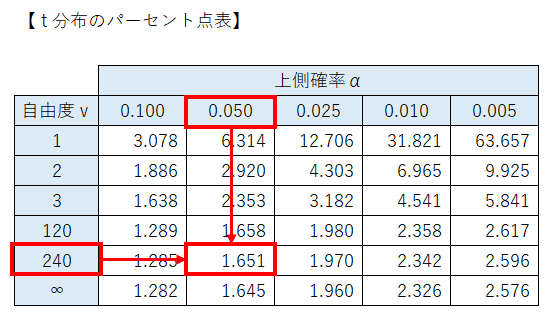
おーっと、自由度$${195}$$が表に無いです！
$${240}$$で代用しましょう。
パーセント点は約$${1.651}$$です。
それでは、信頼区間の公式に値を当てはめましょう。
$$
\begin{align*}
&傾きの推定値 \pm 自由度(n-p-1)のt分布の上側\alpha/2 \%点 × 傾きの推定値の標準誤差 \\
&=-60.263 \pm 1.651 \times 4.414 \\
&=-60.263 \pm 7.287514 \\
&\fallingdotseq [-67.55, -52.98]
\end{align*}
$$
自由度を近似したことで解は近似値になりました。
この近似値に最も近い回答選択肢は$${[-67.52, -53.00]}$$です。
公式問題集の解説では、自由度$${195}$$の$${t}$$分布は標準正規分布と近似していることから、標準正規分布の上側確率表から上側$${5\%}$$点を取得する考え方が記載されています。
この方法で$${90\%}$$信頼区間を計算してみましょう。
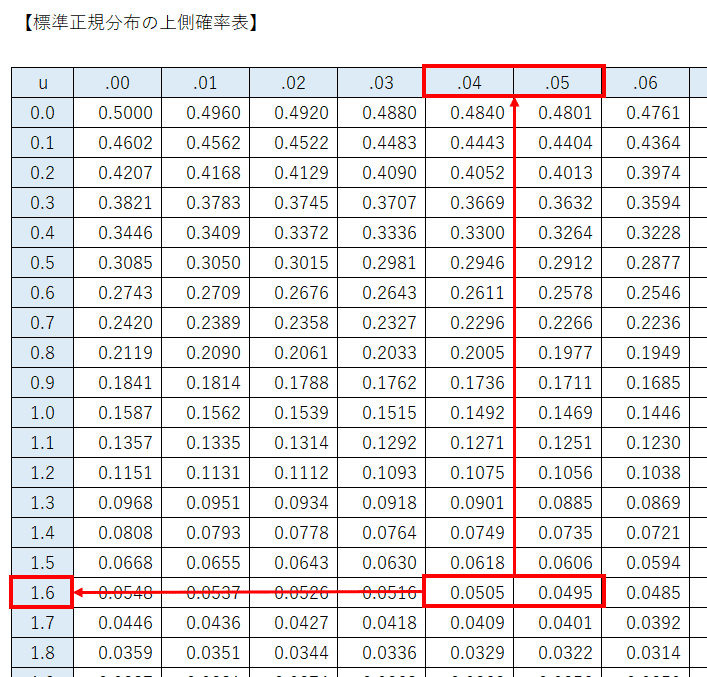
標準正規分布の上側$${5\%}$$点は約$${1.645}$$です。
$$
\begin{align*}
&傾きの推定値 \pm 標準正規分布の上側\alpha/2 \%点 × 傾きの推定値の標準誤差 \\
&=-60.263 \pm 1.645 \times 4.414 \\
&=-60.263 \pm 7.26103 \\
&\fallingdotseq [-67.52, -53.00]
\end{align*}
$$
解答選択肢 ② の値と合致しました。
問３の解答は ② です。
解答
〔1〕④、〔2〕①、〔3〕② です。
難易度 ふつう
・知識：回帰分析の出力結果の読み取り、決定係数、回帰係数の算出、残差の平均値、回帰係数の検定、残差プロット、回帰係数の信頼区間
・計算力：数式組み立て（低）、電卓（低）
・時間目安：3問合計 5分
知る
おしながき
今回はお休みします。
特集記事のお知らせ
単回帰モデルの詳しい学習ポイントを「特集記事」にまとめました。
ぜひご覧くださいませ。
「6. 統計ソフトウェア R の出力結果」の章に「出力結果読み取り」の主要テーマをまとめています。
実践する
今回はお休みします。
特集記事のお知らせ
EXCEL、R、Pythonの単回帰分析の実践を「特集記事」にまとめました。
ぜひご覧くださいませ。
おわりに
今回は「統計ソフトウェア R の出力結果」のさまざま論点に取り組みました。
お時間がありましたら、ぜひ、お手元のデータを R に取り込んで、回帰分析 lm 関数を実行してみましょう！
もちろん Python、EXCEL、統計専用ソフトウェアで回帰分析するのもＯＫです！
特集記事を参考にして動かしてみてくださいね。
【特集記事のリンク】
もしもお手元に適当なデータがない場合は、ネットで回帰分析に利用できるデータを取得してはいかがでしょう。
例えば・・・
「統計を学びたい人へ贈る、統計解析に使えるデータセットまとめ」
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次