
2-6 相関関係の記述 〜 恣意的に抽出した標本の分布
今回の統計トピック
恣意的な基準で標本を抽出するときに、標本の分布が母集団からどのように乖離するのでしょう?
散布図の変化を見ながら確認していきましょう!
ランダムに抽出することの意味合い・大切さに接近できるかもです。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
2変数記述統計の分野
問6 相関関係の記述(国語と英語の試験得点)
試験実施年月
調査中
問題
公式問題集をご参照ください。
解き方
題意
あるデータから一部のデータを抽出する時に、抽出データの相関がどのように変わるかを考察する問題です。
「2-3 散布図の選択」の後続問題に該当します。
相関係数の計算
問題文の次の点に注目します。
散布図は300人全員の国語と英語の得点の分布を示す。
300個の全データのうち「得点の合計が120点以上」のデータを抽出する場合、抽出データの相関はどうなるか。
散布図から読み解きなさい。
この問題は、散布図の中から「120点以上のデータの部分」を特定できるかどうかが、解答の鍵を握っています。
120点以上のデータを特定する
まず、120点の境界線を引いた散布図を見てみましょう。
記事「2-3 散布図の選択」で使用した相関係数$${\boldsymbol{r=0.66}}$$のサンプルデータを用いて確認します。
なお、この散布図は公式問題集のデータと一致するものではないことを、予めお断りいたします。
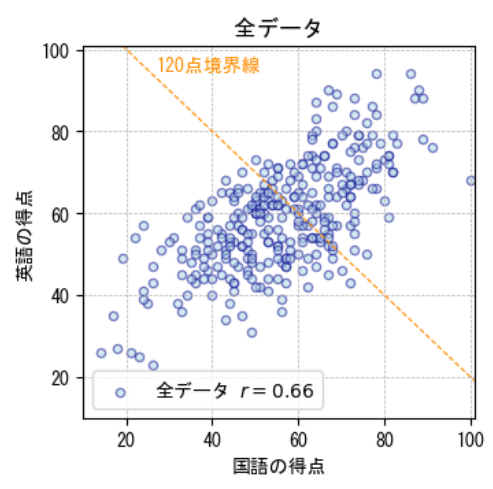
オレンジの120点境界線は、グラフの ( x: 横軸, y: 縦軸 )の2点 ( 0, 120 ) と (120, 0 ) を結ぶ直線です。
120点境界線の右上の点が「合計得点120点以上」のデータです。
300個の全データのような「右肩上がりに帯状に伸びるような形」は無くなり、散らばりの程度が大きくなって、団子のようなかたまりになりました。
300個の全データと比べて、相関が弱くなっていることを示唆しています。
120点以上のデータを取り出した散布図を確認してみます。
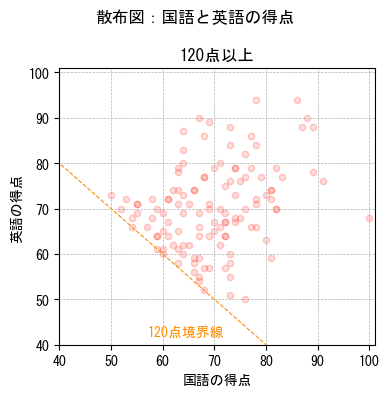
全データと比べて、散らばりが大きくなりました。
散らばりが大きいので相関が弱くなっていると言えます。
①~⑤の選択肢を確認する
問題集の選択肢の中で、相関が弱くなることに言及しているのは、選択肢⑤だけです。
上の散布図を見ると、国語と英語のどちらか一方の科目の得点が高くて、もう一方の科目の得点が低いデータが見られます。
120点以上だけを抽出して形成する標本データでは、母集団のあらゆる統計量がリセットされる感じです。
300個の全データ=母集団の持つ統計量が引き継がれるわけでは無いのです。
平均が変わり、分散や標準偏差が変わり、共分散が変わり、相関係数が変わるのです。
他の選択肢を確認する
■選択肢①
データの抽出方法がいわゆる無作為になっていないので、全データ=母集団の相関に類似するとは限りません。
■選択肢②
得点の高さだけで相関関係が決まるわけではありません。
120点以上を抽出したデータのみで改めて散らばり度合いを確認して、相関の程度を判断する必要があります。
■選択肢③
120点以上を抽出したデータの散布図を見れば、相関の強まり/弱まりを確認できます。
見当がつかない、ということはありません。
■選択肢④
120点以上を抽出したデータの散布図を見ても、国語と英語のどちらか片方だけが高得点という傾向は見られません。
強い負の相関にはならないでしょう。
解答
⑤です。
難易度 ふつう
・知識:相関関係、散布図
・計算力:不要
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
ここでは「ランダムに生成した国語と英語の得点風の数値データ」を用います。
データ数300、相関係数0.66、国語の平均は56点、英語の平均は59点です。
データの生成には「フリーの統計分析プログラムHAD」(EXCEL VBA)を利用しました。
ありがとうございます!
今回は、標本抽出をさまざまな方法で実施して、母集団の相関係数と標本の相関係数の変化を散布図にて確認します。
相関係数と散布図
📕公式テキスト:1.6.1 散布図(26ページ~)、1.6.2 相関係数(29ページ~)
①120点以上を抽出
公式問題集と同じ抽出方法「合計得点が120点以上を抽出」です。
散布図を次の3パターンで作成しています。
・300個の「全データ」
・「120点以上」を抽出
・「全データと120以上」の両方

凡例の「$${ r=}$$ 」の数値が相関係数です。
120点以上を抽出したデータの相関係数は 0.29 です。
全データの相関係数 0.66 よりも相関が弱くなっています。
②ランダム抽出
いわゆる無作為非復元抽出法で100個のデータを抽出しました。

中央のランダムに抽出したデータの散布図は、全データの散布図に似ています。
相関係数も近似しています。
要約統計量を見てみましょう。

両方のデータの相関係数、共分散、平均(mean)、標準偏差(std)はよく似ています。
全データを母集団とすると、ランダムに抽出した100個の標本(サンプル)は、母集団の様子をうまく表現できているような感じです。
③四分位範囲を抽出
合計得点の中央にあたる25%点~75%点の範囲(四分位範囲)を抽出しました。

まったく形状の異なる散布図になりました。
四分位範囲を抽出したデータの相関係数は -0.22 。
負の相関になりました。偶然だとは思いますが、面白いですね。
両データの箱ひげ図を見てみましょう。

四分位範囲を抽出したデータのほうが、データの範囲が狭くなっていて、「真ん中にギュッと集まった」感じがします。
散らばりの程度が抑えられて、弱い相関になっていることが箱ひげ図でも確認できました。
④上位50個+下位50個を抽出
合計得点の上位50個、下位50個を抽出しました。

左と中央の散布図を比較すると、データの分布の様子は全く異なります。
相関係数は 0.85 となり、相関が強くなりました。
要約統計量を確認します。

両者の平均(mean)は近い値ですが、共分散の値が上位+下位の方が大きくなりました。
データ各点が平均と大きく乖離(偏差)したことで、共分散が大きくなったと想定されます。
⑤IDを3番ごとに抽出
ID番号の3番から始めて、ID6番、ID9番・・・のような「3つごとに」100個のデータを抽出しました。
系統抽出法に似ている抽出方法です。
系統抽出法は、まず母集団の個体全てに番号をつける。次に第1番目の個体を無作為に抽出し、第2番目以降は番号について同じ間隔で抽出するという方法である。
今回の抽出は第1番目の個体を意図して3番に決めているので、無作為抽出ではありません。
第2番目以降は番号=IDを同じ間隔(3つ)で抽出しています。

3番ごとに抽出したデータの散布図(中央)のバラツキは全データのバラツキに似ている感じがします。
相関係数は 0.59 。少し相関が弱まったようです。
まとめ
さまざまな抽出方法でデータの一部を切り取って、相関の様子を確認しました。
②ランダム抽出や⑤系統抽出的な方法では、母集団の相関を維持してデータを抽出できたようです。
一方で、データの中身である「得点」に関わらせて、①120点以上、③四分位範囲、④上位+下位などといった「ランダムでない」方法で抽出する場合、相関がガラリと変わりました。
予告
次回の記事から「標本抽出法」のテーマに移ります。
ずばり、母集団から標本を抽出する方法について深掘りします。
今回の記事を思い出して、さまざまな抽出方法の結果のイメージが湧いていると、標本抽出法の理解がいっそう深まると思います!
実践する
データを抽出して散布図などの変化を確認してみよう
「知る」で利用した「ランダムに生成した国語と英語の得点風の数値データ」から一部のデータを抽出して、相関係数や散布図のプロットが変化する様子を確認しましょう。
シミュレーションのご紹介
EXCELファイルをダウンロードして、データ抽出のシミュレーションを実施しましょう。
データは、素データ、120点以上データ、シミュレーション枠6つの8つあります。
シミュレーション枠にA~Fまで名付けました。
シミュレーション枠の値を変更すると、右側の散布図が変化する仕組みになっています。

下の図のように、シミュレーション枠のデータの一部を消します。
「残したデータを抽出したデータとみなす」という方法でデータ抽出を行います。

「残りのデータの散布図」と「素データの散布図」を比べることによって、
抽出データ=標本データの分布が母集団の分布と近似するか、乖離するかを確認できます。
「120点以上を抽出」枠は、「素データ」(全データ)から合計得点が120点以上のデータのみを抽出して、設定しています。
データ抽出の一例として扱ってください。
データの抽出に連動して変化する散布図・相関係数を確認しましょう。
EXCELファイルのダウンロード
こちらのリンクからEXCELファイルをダウンロードできます。
CSVファイルのダウンロード
こちらのリンクから素データのCSVファイルをダウンロードできます。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
電卓・手作業で作成してみよう!
今回はお休みです。
EXCELで作成してみよう!
上述の「データを抽出して散布図などの変化を確認してみよう」を実践します。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、「知る」の章で使用した図表の作成に取り組みます。
①ライブラリのインポート
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②要約統計量・グラフ作成関数の定義
要約統計量と散布図を作成する共通関数の定義です。
def draw_all(df_in, title):
# 共通の設定
reg = LinearRegression()
corr_all = df.corr().values[0][1]
corr_part = df_in.corr().values[0][1]
# 要約統計量の表示
print(f'--- {title}データの要約統計量 ---')
print(f'相関係数: {corr_part:.2f}')
print(f'共分散: {df_in.cov().values[0][1]:.2f}')
display(df_in.describe())
# グラフ用の共通設定
x_col, y_col = '国語の得点', '英語の得点'
args_all = {'s': 20, 'c': 'lightblue', 'ec': 'darkblue',
'alpha': 0.5, 'label': f'全データ $r={corr_all:.2f}$'}
args_part = {'s': 20, 'c': 'tomato', 'ec': 'red',
'alpha': 0.2, 'label': f'{title} $r={corr_part:.2f}$'}
x120, y120 = (0, 120), (120, 0)
### 描画
fig, ax = plt.subplots(1, 3, figsize=(10, 4), constrained_layout=True,
sharex='all', sharey='all')
### ALLのプロット
ax[0].scatter(df[x_col], df[y_col], **args_all)
# 120点のボーダー線
ax[0].plot(x120, y120, lw=0.8, ls='--', c='darkorange')
ax[0].text(27, 95, '120点境界線', c='darkorange')
# 修飾
ax[0].set_title('全データ')
ax[0].set_xlim([10, 101])
ax[0].set_ylim([10, 101])
ax[0].set_xlabel(x_col)
ax[0].set_ylabel(y_col)
ax[0].grid(axis='both', linewidth=0.5, linestyle='--')
ax[0].legend(loc='best')
### PARTのプロット
ax[1].scatter(df_in[x_col], df_in[y_col], **args_part)
# 120点のボーダー線
ax[1].plot(x120, y120, lw=0.8, ls='--', c='darkorange')
ax[1].text(27, 95, '120点境界線', c='darkorange')
# 修飾
ax[1].set_title(title)
ax[1].set_xlabel(x_col)
ax[1].grid(axis='both', linewidth=0.5, linestyle='--')
ax[1].legend(loc='best')
### ALL + PARTのプロット
ax[2].scatter(df[x_col], df[y_col], **args_all)
ax[2].scatter(df_in[x_col], df_in[y_col], **args_part)
# ALLの回帰直線
x, y = df[[x_col]], df[[y_col]]
reg.fit(x, y)
y_pred = reg.predict(x)
ax[2].plot(x, y_pred, c='darkblue', lw=0.5)
# PARTの回帰直線
x, y = df_in[[x_col]], df_in[[y_col]]
reg.fit(x, y)
y_pred = reg.predict(x)
ax[2].plot(x, y_pred, c='red', lw=0.5)
# 120点のボーダー線
ax[2].plot(x120, y120, lw=0.8, ls='--', c='darkorange')
ax[2].text(27, 95, '120点境界線', c='darkorange')
# 修飾
ax[2].set_title(f'全データと{title}')
ax[2].set_xlabel(x_col)
ax[2].grid(axis='both', linewidth=0.5, linestyle='--')
ax[2].legend(loc='best')
# plt全体の修飾
plt.suptitle('散布図:国語と英語の得点($r$は相関係数)')
plt.legend()
plt.tight_layout()
# plt.savefig(f'./scatter_{title}.png') # グラフ画像ファイルの保存
plt.show()③CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile, index_col='ID')
print(df.shape)
display(df.head())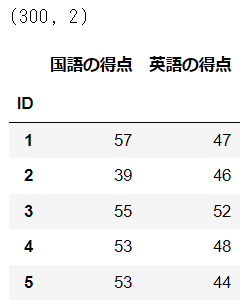
④全データの統計量
読み込んだデータの要約統計量を表示します。
print(f'--- 全データの要約統計量 ---')
print(f'相関係数: {df.corr().values[0][1]:.2f}')
print(f'共分散: {df.cov().values[0][1]:.2f}')
display(df.describe())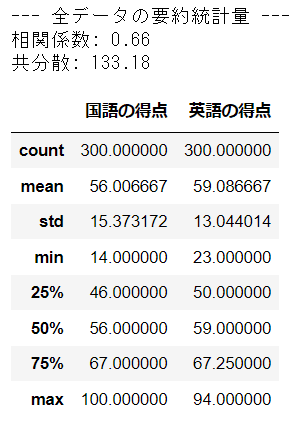
⑤120点以上を抽出
合計得点が120点以上のデータを抽出したデータフレームを作成して、要約統計量・散布図を作成します。
# データフレームの作成
df120 = df[df['国語の得点']+df['英語の得点'] >= 120]
print(df120.shape)
display(df120.head())
# 描画
draw_all(df120, '120点以上')
⑥ランダムに100件を抽出
ランダムに100件を抽出したデータフレームを作成して、要約統計量・散布図を作成します。
pandasのsampleでランダムサンプリングしました。
引数random_state=123の123の部分を他の数字に変更すると、抽出データを変えることができます。
# データフレームの作成
df_random = df.sample(n=100, axis=0, replace=False, random_state=123)
print(df_random.shape)
df_random.head()
# 描画
draw_all(df_random, 'ランダム抽出')
⑦四分位範囲内のデータを抽出
合計得点が四分位範囲に含まれるデータ154件を抽出したデータフレームを作成して、要約統計量・散布図を作成します。
pandasのquantileを利用して、合計得点の第1四分位点と第3四分位点を取得します。
# データフレームの作成
q1 = df.sum(axis=1).quantile(q=0.25) # 第1四分位点
q3 = df.sum(axis=1).quantile(q=0.75) # 第3四分位点
# print(q1, q3)
df_iqr = df[(df.sum(axis=1) >= q1) &(df.sum(axis=1) <= q3)]
print(df_iqr.shape)
display(df_iqr.head())
# 描画
draw_all(df_iqr, '四分位範囲抽出')
⑧上位50データ+下位50データを抽出
合計得点の上位50件と下位50件を抽出したデータフレームを作成して、要約統計量・散布図を作成します。
pandasのnlargestで上位を、nsmallestで下位を抽出します。
df_upper_lower = pd.concat([df.iloc[df.sum(axis=1).nlargest(50).index-1],
df.iloc[df.sum(axis=1).nsmallest(50).index-1]])
print(df_upper_lower.shape)
display(df_upper_lower.head())
# 描画
draw_all(df_upper_lower, '上位+下位')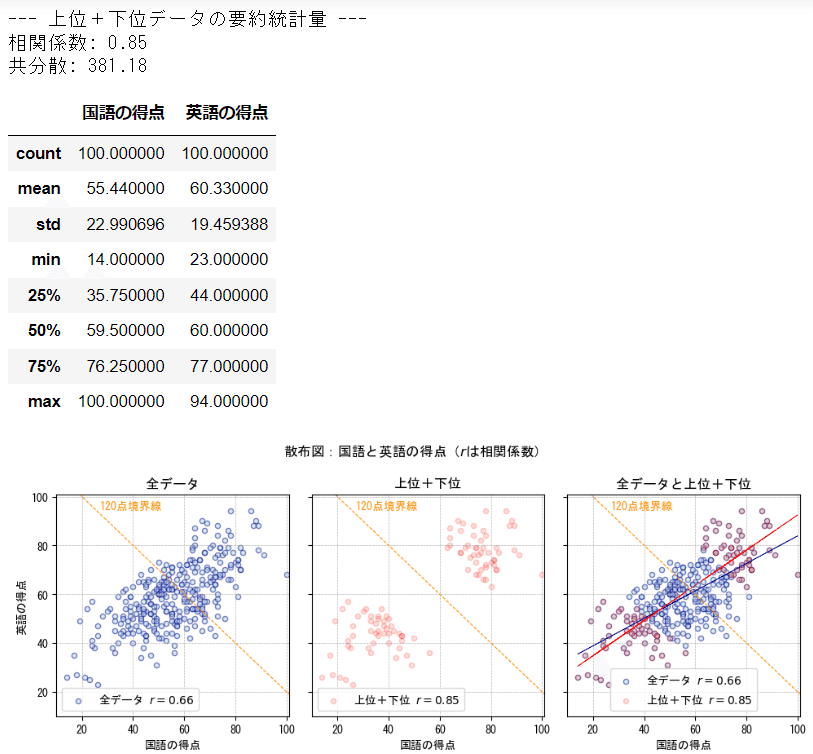
⑨IDが3の倍数のデータ100件を抽出
IDの3番から3番ごとに100件を抽出したデータフレームを作成して、要約統計量・散布図を作成します。
スライスで開始位置 2(1件目の位置は0)とステップ 3を指定します。
# データフレームの作成
df_step3 = df.iloc[2::3]
print(df_step3.shape)
display(df_step3.head())
# 描画
draw_all(df_step3, '3番ごとに抽出')
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
「2変数記述統計の分野」はこの記事で終わります。
散布図と相関係数がいっぱいの分野でした。
XとYの2つの変数があると、2つの関係性を知りたくなります。
散布図や相関係数に加えて、今回のグラフにはこっそり回帰直線をプロットしました。
Xに一定の係数を掛けて、一定の定数値(傾き)を加えて、Yの値を算出する、回帰直線はこんな感じです。
$${y=\alpha + \beta x}$$と記述します。
$${x}$$は説明変数、$${y}$$は応答変数・目的変数です。
説明変数が1つだけの場合は単回帰と呼ばれます。
2つ以上になると重回帰に変身します。
詳しくは「10 線形モデルの分野」で回帰分析を取り扱います。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
