見出し画像

2-1 散布図と度数分布 〜 グラフを描く

ネイピア DS

今回の統計トピック

散布図、度数分布表、ヒストグラムを作成して、この３種の図表の関係性を深掘りします！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

2変数記述統計の分野
問1 散布図と度数分布（50歳時未婚率）

試験実施年月
統計検定2級 2019年11月 問2（回答番号5）

問題

公式問題集をご参照ください。

解き方

題意
散布図は、横軸が男性の50歳時未婚率（%）、縦軸が女性の50歳時未婚率（%）です。
問題は、「散布図の縦軸の女性50歳時未婚率（%）部分をヒストグラムにすると、選択肢のどのヒストグラムに該当するか」を出題しています。
散布図の2変数のうち「1変数を取り出して」、ヒストグラムをつくるイメージです。

目盛りの間隔（階級）の確認
散布図の縦軸の目盛りの間隔とヒストグラムの間隔（階級）の一致性を確認します。
散布図には最下限と最上限の目盛りが記載されていないのですが、目盛りの間隔から推測できそうです。

定規のイラスト（文房具）：「いらすとや」さんより

散布図の縦軸間隔（%）は、(1)8～10、(2)10～12、(3)12～14、(4)14～16、(5)16～18、(6)18～20、の６つ。
ヒストグラムの階級（%）は、(1)8～10、(2)10～12、(3)12～14、(4)14～16、(5)16～18、(6)18～20、に加えて、(7)20～22があります。

散布図とヒストグラムの間隔は 2% 幅で一致しています。
ただし、ヒストグラムの(7)20～22%に当たる点は散布図の縦軸には存在しません。
女性の50歳時未婚率が20%以上の都道府県は無い、ということです。
つまり、20～22%階級に1以上の度数があるヒストグラム④⑤は適切ではありません。

散布図の縦軸の目盛り幅ごとに点を数える
(1)から(6)の散布図の幅ごとに点をカウントした数が、ヒストグラムの各階級の度数になります。

まず、点の少なそうな階級から始める
8～10%の階級には点が2個～4個該当しそうです。
ヒストグラムのうち、8～10%の階級に度数があるのは①と③です。
つまり、8～10%の階級の度数が0のヒストグラム②は適切ではありません。

残りのヒストグラム①③の違いを見る
ヒストグラム①と③を比べると、10～12%の階級の度数が大きく異なります。
①の度数は 4、③の度数は 12、くらいでしょう。
散布図の縦軸10～12%の点をカウントしてみましょう。
少なく見積もっても、5つ以上の点がありそうです。
つまり、10～12%の階級の度数が4のヒストグラム①は適切ではありません。

旅日記で使えるいろいろなマーク：「いらすとや」さんより

まとめ
残りのヒストグラム③が適切ということになります。
散布図と度数分布表の特徴を捉えて、消去法で選択肢を絞り込みました。

解答

①です。

難易度　やさしい

・知識：散布図、ヒストグラム、度数分布表
・計算力：不要
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
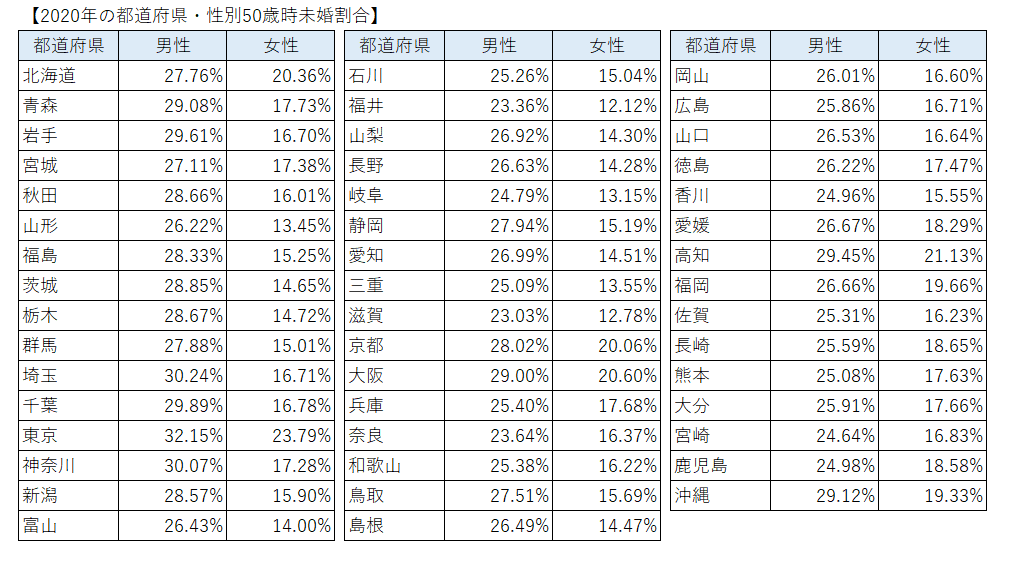
ここでは、2020年の「都道府県・性別50歳時未婚割合」（単位：%）を参照データとして利用します。
未婚は「まだ結婚したことのない人」のことです。

参照データ

【出典記載】
出典：「人口統計資料集(2022年度版)」（国立社会保障・人口問題研究所）（https://www.ipss.go.jp/syoushika/tohkei/Popular/Popular2022.asp?chap=0）
【コンテンツ編集・加工の記載】
記事の記載にあたっては、「人口統計資料集(2022年度版)」（国立社会保障・人口問題研究所）を加工して作成しています。（https://www.ipss.go.jp/syoushika/tohkei/Popular/Popular2022.asp?chap=0）

今回は散布図、度数分布表、ヒストグラムの作成に取り組みながら、素データとこれらの図表の繋がりを体感することを目指します。

散布図

📕公式テキスト：1.6.1 散布図（26ページ～）
散布図はデータの２つの項目ペアをグラフにプロットするものです。
１つ目の項目を横軸（ x 軸）、もう１つの項目を縦軸（ y 軸）に合わせて、グラフの平面に点を記します。

散布図の作成
次の図は、参照データの表から散布図を作成する作業の一部を表しています。
表の北海道：男性・女性のデータペアを散布図の「横軸 27.76%、縦軸 20.36%」にプロットします。

散布図の作成作業イメージ

47都道府県の点をプロットし終えると、散布図の完成です。
散布図の完成サンプルです。

散布図サンプル

度数分布表

📕公式テキスト：1.2.1 ヒストグラムの作成（6ページ～）等
度数分布表は「1変数」を要約記述する表です。
「階級」と呼ぶ幅（以上、未満）ごとに、データの個数をカウントした「度数」をまとめた表です。

度数分布表の作成
参照データの変数には、横軸の「男性」、縦軸の「女性」の２つがあります。
男性と女性のそれぞれで度数分布表を作成します。

階級の幅は、各データの最小値・最大値を把握して、バランスを見ます。
今回は、問題と同じ 2% 区切りの偶数値にしましょう。
男性は 22% から 34％ までを 2% 刻みで、女性は 12% から 24％ までを 2% 刻みで、階級を設定します。

データの最小値・最大値を確認

男性の22%以上24%未満の階級を例にして、度数の数え方を確認します。
参照データの男性の列から、22%以上24%未満に該当する都道府県の数をカウントします。
福井県、滋賀県、奈良県の３県がヒットしました。
22%以上24%未満の度数は「 3 」です。

手作業の場合、参照データの個数を数えて度数分布表をつくる

男性の度数分布表は次のようになります。

度数分布表サンプル１

女性の度数分布表は次のようになります。

度数分布表サンプル２

累積度数は、度数を上から順に累積計算した値です。
相対度数は、各階級の度数を度数の合計（ここでは47）で割った値です。
累積相対度数は、相対度数を上から順に累積計算した値です。

ヒストグラム

📕公式テキスト：1.2.1 ヒストグラムの作成（6ページ～）
「ヒストグラム」は度数分布表と表裏一体のグラフです。
度数分布表の階級ごとに階級値を棒グラフに似たグラフで表現します。

度数分布表からヒストグラムを作成してみます。
階級（以上・未満の幅）ごとに度数の棒グラフを作る要領です。

ヒストグラムサンプル

棒の上に度数を記載しています。
度数分布表の度数と比べて、一致することを確認しました。

散布図のカウント値とヒストグラムを比べる
公式問題集の問題と同じように、散布図の点の数をカウントして、度数分布表の度数と比べてみます。

散布図の点を数える

この図では、左側に横軸＝男性のカウント値、右側に縦軸＝女性のカウント値を表しています。
度数分布表の度数と一致することを確認できました。

旅日記で使えるいろいろなマーク

まとめ

  • 散布図を横軸で切り出すと度数分布表／ヒストグラムとの繋がりを確認でき、縦軸で切り出すともう一つの度数分布表／ヒストグラムとの繋がりを確認できることが分かりました。

  • 散布図の横軸・縦軸の２次元データを「横軸の１次元データ」と「縦軸の１次元データ」に切り分ける感じです。

  • 素の参照データ自体が男性軸と女性軸の２次元データであり、男性の１次元を切り出して度数分布表／ヒストグラムを作り、女性の１次元を切り出してもう一つの度数分布表／ヒストグラムを作れることが分かりました。


実践する

散布図、度数分布表、ヒストグラムを描いてみよう

「都道府県・性別50歳時未婚割合」の参照データは国立社会保障・人口問題研究所のホームページで公開されています。

日本の人口のイラスト：「いらすとや」さんより

次のリンクで2022年度版「人口統計資料集」の目次を確認できます。

次のリンクでEXCELファイルをダウンロードできます。
「表１２－３７ 都道府県，性別50歳時未婚割合：1920～2020年」です。
男性のページと女性のページが分かれています。


CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
2015年と2020年の配偶関係不詳補完結果に基づくデータです。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。


電卓・手作業で作成してみよう！

「知る」の内容を手作業で実践しましょう！
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
データやグラフ間の関係も実感できると思います。


EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

散布図の作成
EXCELの散布図グラフを利用します。
参照データの表より、男性データと女性データを範囲指定します。
メニューの「挿入」を選び、「グラフ」の右下隅の矢印をクリック、「グラフの挿入」画面で散布図を選択します。

EXCEL：散布図の選択画面イメージ

散布図の点に都道府県名を設定する方法です。
グラフをクリックして表示される「＋」メニューの階層をたどって「その他のオプション」を指定します。

EXCEL：グラフの＋メニュー

「データラベルの書式設定」画面で「セルの値」のチェックボックスをチェックして、隣の「範囲の選択」ボタンを押します。
「データラベル範囲」画面で都道府県名のセル範囲を設定します。

EXCEL：散布図のデータラベルを表示する

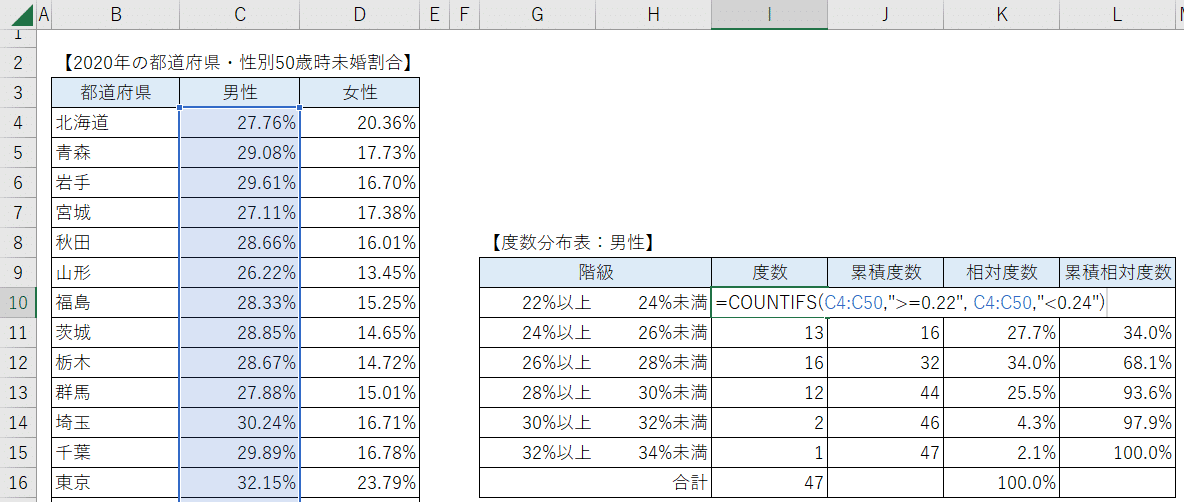
度数分布表の作成
この度数分布表の階級は「◯◯以上、◯◯未満」です。
EXCELの度数カウント用の関数「FREQUENCY関数」は「◯◯超、◯◯以下」になり、今回の度数分布表に合いません。
そこで、「COUNTIFS関数」を利用して度数をカウントします。
COUNTIFS関数（末尾にS有り）は「複数の条件を設定」できる点で、COUNTIF関数（末尾にS無し）よりも複雑な検索ができます。

=COUNTIFS( 検索範囲1, 検索範囲1に適用する条件式, 検索範囲2, 検索範囲2に適用する条件式)

EXCEL：COUNTIFS関数による度数のカウント

ヒストグラムの作成
EXCELの棒グラフを利用します。

EXCEL：棒グラフサンプル

棒グラフの棒の横幅の調整方法です。
棒グラフの棒をダブルクリックして「データ系列の書式設定」画面を表示します。
「要素の間隔」を 5% 程度にするとヒストグラムのような雰囲気になります。

EXCEL：棒グラフの棒の幅の調整

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。


Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回はいろんな描画系ライブラリを利用して、散布図、度数分布表、ヒストグラムの作成に取り組んでみましょう。

①ライブラリのインポート
データ可視化ライブラリseabornを使用します。

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline

②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。

datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile)
print(df.shape)
display(df.head())
出力イメージ

③散布図の表示
matplotlibのscatterを利用して散布図を描画します。
plt.scatter( x軸のデータ, y軸のデータ, その他の引数 ) です。
また、冒頭の means の箇所で算出した平均値を、散布図にプロットします。

# 単純平均の設定
means = {'2020年_男性': df['2020年_男性'].mean(), 
         '2020年_女性': df['2020年_女性'].mean(),
        }

# scatter引数の設定
args_2020 = {'s': 40, 'c': 'lightblue', 'ec': 'darkblue', 'lw':0.7, 
            'alpha': 0.5, 'label': '2020年'}
args_mean = {'s': 200, 'c': 'yellow', 'ec': 'darkorange', 
            'marker': '*', 'label': '単純平均'}

plt.figure(figsize=(4, 4), tight_layout=True)

# 2020年の散布図のプロット
plt.scatter(df['2020年_男性'], df['2020年_女性'], **args_2020)
plt.scatter(means['2020年_男性'], means['2020年_女性'], **args_mean)
plt.xlim(0.22, 0.34)
plt.ylim(0.10, 0.26)
plt.grid(axis='both', linewidth=0.5, linestyle='--')
plt.title('散布図：2020年都道府県別50歳時未婚割合')
plt.xlabel('男性')
plt.ylabel('女性')
plt.legend(loc='upper left')

# plt.savefig('./scatter.png') # グラフ画像ファイルの保存
plt.show()
出力イメージ

④度数分布表の作成、ヒストグラムの表示１
度数分布表のデータフレームを作成する関数を定義します。
男性・女性の別に度数分布表データフレームを作成します。
pandasのplotを利用して度数分布表データフレームのヒストグラムを作成します。

■度数分布表作成関数の定義
入力したデータフレームのデータに基づいて、度数分布表データフレームを作成する関数です。

# 度数分布表作成関数の定義
def get_freq_table(data, bins):
    freq = pd.cut(data, bins, right=False).value_counts(sort=False)
    class_value = np.round((bins[:-1] + bins[1:]) / 2, 2)
    rel_freq = round(freq / data.count() * 100, 1)
    cum_freq = freq.cumsum()
    cum_rel_freq = rel_freq.cumsum()
    df_freq = pd.DataFrame({
                            '階級以上': np.round(bins[:-1], 2), 
                            '階級未満': np.round(bins[1:], 2),
                            '階級値': np.round(class_value, 2), 
                            '度数': freq, '累積度数': cum_freq,
                            '相対度数': rel_freq, '累積相対度数': cum_rel_freq},
                            index=freq.index)
    return df_freq

■共通引数の設定
次のコードの「df_men_2020.plot.bar(**args_bar) 」で利用する引数を設定します。

# df.plot.barの共通引数の設定
args_bar = {'x':'階級未満', 'y':'度数', 'figsize': (4, 2), 'width': 1,
            'ec': 'white'}

■度数分布表・ヒストグラムの作成／表示（2020年・男性）
上段で関数を呼び出しして度数分布表を作成・表示します。
中段のdf_men_2020.plot.bar(**args_bar) の部分で、Pandasのplot.barを利用してヒストグラム（棒グラフ）を描画します。

# 2020年－男性の度数分布表dfの作成、度数分布表・ヒストグラムの表示
data = df['2020年_男性']
bins = np.linspace(0.22, 0.34, 7)
df_men_2020 = get_freq_table(data, bins)

print('【度数分布表：都道府県別50歳時未婚割合－2020年 男性】')
display(df_men_2020)
df_men_2020.plot.bar(**args_bar)

plt.tight_layout()
# plt.savefig('./bar_2020_men.png') # グラフ画像ファイルの保存
plt.show()
出力イメージ

■度数分布表・ヒストグラムの作成／表示（2020年・女性）

# 2020年－女性の度数分布表dfの作成、度数分布表・ヒストグラムの表示
data = df['2020年_女性']
bins = np.linspace(0.12, 0.24, 7)
df_women_2020 = get_freq_table(data, bins)

print('【度数分布表：都道府県別50歳時未婚割合－2020年 女性】')
display(df_women_2020)
df_women_2020.plot.bar(**args_bar)

plt.tight_layout()
# plt.savefig('./bar_2020_women.png') # グラフ画像ファイルの保存
plt.show()
出力イメージ

⑤ヒストグラムの表示２
matplotlibのhistを利用してヒストグラムを表示します。
入力データのデータフレームdfを使用します。

２つのグラフを横並びにするため、最初のコードで ax に「1, 2」（１行２列）のサブプロットを定義しています。
サブプロット領域は ax[0] と ax[1] に分かれます。
また、sharey=True を指定して、縦軸（y軸）の目盛りを共有しています。

fig, ax = plt.subplots(1, 2, figsize=(6, 3), tight_layout=True, sharey=True)

# 2020年・男性のヒストグラムのプロット
ax[0].hist(df['2020年_男性'], bins=6, range=(0.22, 0.34), ec='white')
ax[0].set_title('2020年 男性', fontsize=10)
ax[0].set_xticks(np.arange(0.22, 0.35, 0.02))

# 2020年・女性のヒストグラムのプロット
ax[1].hist(df['2020年_女性'], bins=6, range=(0.12, 0.24), ec='white')
ax[1].set_title('2020年 女性', fontsize=10)
ax[1].set_xticks(np.arange(0.12, 0.25, 0.02))

fig.supxlabel('割合')
fig.supylabel('都道府県数（度数）')
fig.suptitle('ヒストグラム：都道府県別50歳時未婚割合')

# plt.savefig('./hist.png') # グラフ画像ファイルの保存
plt.show()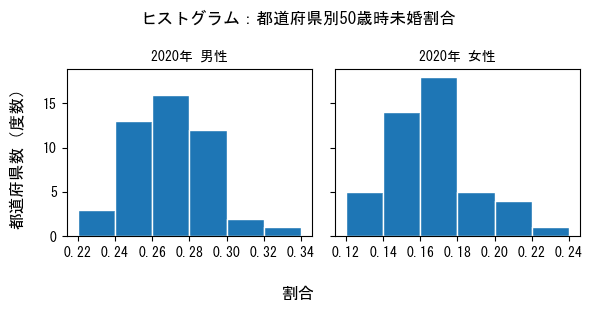
出力イメージ

⑥ジョイントプロットの表示
seabornのjointplotを利用して、散布図とヒストグラムの両方を表示します。
kind='scatter' の設定で散布図を選択しています。
入力データのデータフレームdfを使用します。

「２つの変数の相関の様子を散布図で確認」でき、同時に、それぞれ「１つの変数の分布の様子をヒストグラムで確認」できます。
データから気づきを得たいとき、ジョイントプロットは役立ちそうです！

#ヒストグラム付きの散布図を作成
sns.jointplot(data=df, x='2020年_男性', y='2020年_女性', kind='scatter',
              height=5, ratio=2, marginal_ticks=True, color='steelblue')
plt.suptitle('ジョイントプロット：都道府県別50歳時未婚割合（2020年）')
plt.tight_layout()
# plt.savefig('./jointplot.png') # グラフ画像ファイルの保存
plt.show()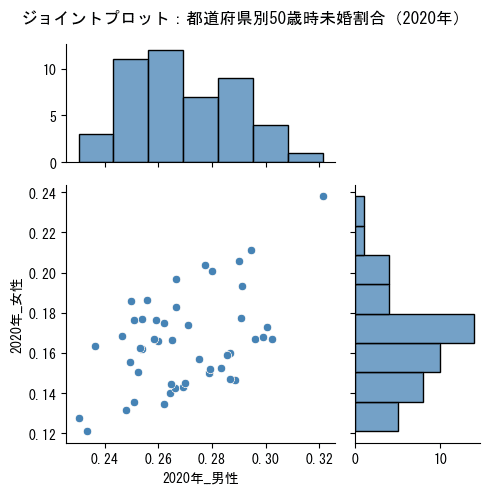
出力イメージ

■グラフを作成してみて
Pythonのグラフ描画のツールをいくつか利用してみました。
pandasのデータフレームを使う場合はpandasのplotが便利そうです。
気軽に表現力の高い描画をする場合はseabornでしょう。
細かな設定を行う場合はmatplotlibがよさそうです。
今回利用したもの以外にもツールがあるそうです。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。


おわりに

今回から「2変数記述統計の分野」が始まりました。
この分野は全部で６問あるのですが、そのうち５問で散布図が出現します！
特に後半の問題では、「散布図、共分散、相関係数が一体」になった問題が出題されます。
2変数の関係の理解を促進できるように、がんばって書きます！
引き続きよろしくお願いいたします。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

目次

いいなと思ったら応援しよう！