
2-3 散布図の選択 〜 素データから相関係数を逐一計算
今回の統計トピック
相関係数の計算と散布図の作成を通じて、2つのデータの相関関係に迫ります!
散布図を見て、おおよその相関係数を掴めるようになれるかもです!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
2変数記述統計の分野
問3 散布図の選択(国語と英語の試験得点)
試験実施年月
調査中
問題
公式問題集をご参照ください。
解き方
題意
①相関係数の計算と②相関係数と散布図の関係の2つを問う内容になっています。
相関係数の計算
問題文の次の点に注目します。
国語の得点の分散 236.6
英語の得点の分散 170.1
国語の得点と英語の得点の共分散 133.1
相関係数の公式$${相関係数=\cfrac{確率変数XとYの共分散}{\sqrt{Xの分散\times Yの分散}}}$$に当てはめて、相関係数を算出します。
$$
\begin{align*}
相関係数&=\cfrac{国語と英語の共分散}{\sqrt{国語の分散\times英語の分散}}\\
&=\cfrac{133.1}{\sqrt{236.6\times170.1}}\\
&=0.663\cdots\\ \fallingdotseq 0.66
\end{align*}
$$
相関係数は 0.66 です。

相関係数と散布図の関係
相関係数 0.66 は、「正の値」であり、かつ、「中程度の値の大きさ」です。
このデータは、散布図に次のように表されます。
・相関係数が正の値=右肩上がり
・相関係数の値の大きさが中程度=右肩上がりの傾向が強からず・弱からず
(この散布じゃない・・・)
さて、解答の選択肢を1つ1つ確認します。
選択肢① 適切である
「右肩上がり」の傾向が「ややはっきり」出ています。
この特徴は、中程度の正の相関です。
相関係数は 0.6 程度と思われます。
正の傾向の強さ・弱さは選択肢⑤、選択肢④と比べるとイメージしやすいかもしれません。
選択肢② 適切でない
右肩上がりの傾向も左肩上がりの傾向も見られません。
この特徴は、無相関を示しています。
相関係数はゼロに近い値と思われます。
選択肢③ 適切でない
「右肩上がり」の傾向が「強くはっきり」出ています。
この特徴は、強い正の相関です。
相関係数は 0.9 程度と思われます。
選択肢④ 適切でない
「右肩上がり」の傾向が「弱くうっすら」出ています。
この特徴は、弱い正の相関です。
相関係数は 0.4 程度と思われます。
選択肢⑤ 適切でない
「左肩上がり」の傾向が「強くはっきり」出ています。
この特徴は、強い負の相関です。
相関係数は -0.9 程度と思われます。
解答
①です。
難易度 やさしい
・知識:相関係数、散布図
・計算力:数式組み立て(低)、電卓(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
ここでは「ランダムに生成した国語と英語の得点風の数値」データを用いて、相関係数と散布図の組み合わせを学びましょう。
【データの概要】
次の「相関係数8ケース」に相当する「国語と英語のペア」を各300個用意しました。
・相関係数が正:0.90、0.66、0.44、0.03
・相関係数が負:-0.90、-0.66、-0.44、-0.03
国語の平均は56点付近、英語の平均は59点付近になるように作成しました。
データでは国語をx、英語をyと表します。

【謝辞】
「フリーの統計分析プログラムHAD」(EXCEL VBA)を利用してデータを作成しました。
「特定の共分散の値に合致する乱数データ」を手作業で作るのは、ほぼ無理です(泣)
このツールが無かったら、記事を書けませんでした。
誠にありがとうございます!
今回は相関係数と散布図の関係を見てから、相関係数の計算に取り組みます。
相関係数と散布図
📕公式テキスト:1.6.1 散布図(26ページ~)
相関
国語の得点と英語の得点の関係のように、変数間の関係を相関と呼びます。
次のグラフで相関係数と散布図の見え方を確認しましょう。
(宇宙の星雲にようにも見えます🛸)

横軸(x軸)に国語の得点、縦軸(y軸)に英語の得点をプロットしています。
各グラフに300の点がプロットされています。
グラフ上部の「相関係数$${r=\cdots}$$の値」と「グラフの点が構成する形状」に注目しましょう。
正の相関、負の相関
上段が正の相関、下段が負の相関です。
一方の値が大きくなると他方の値も大きくなる傾向は正の相関です。
右肩上がりの形状は正の相関です。
このとき、相関関数$${\boldsymbol{r}}$$の値は正です。
一方の値が大きくなると他方の値が小さくなる傾向は負の相関です。
左肩上がりの形状は負の相関です。
このとき、相関関数$${\boldsymbol{r}}$$の値は負です。
2つの変数間に特別な関係がない場合は無相関です。
このとき、相関関数$${\boldsymbol{r}}$$の値はゼロに近くなります。
相関の強さ
グラフの左が強い相関、右が弱い相関です。
強い相関は一方向の傾向がくっきりと散布図に現れます。
相関が弱くなるにつれて、傾向が曖昧になる様子を散布図から読み取ることができます。
相関係数$${r}$$の絶対値が 0.9 の場合、強い相関と言えそうです。
相関係数$${r}$$の絶対値が 0.66 の場合、中程度の相関と言えそうです。
相関係数$${r}$$の絶対値が 0.44 の場合、弱い相関と言えそうです。
相関係数$${r}$$の絶対値が 0.03 の場合、無相関と言えそうです。

相関係数の計算
前項では、散布図サンプルを用いて直感的に、2つの変数の相関係数の程度と、相関係数に応じた散布図の見え方を確認しました。
ここからは、相関係数の数値の成り立ちと計算式を追っていきます。
1つの変数の平均・分散・標準偏差と、2つの変数間の共分散を確認しつつ、相関係数を計算します。
データ数を10個に減らした簡単なサンプルを用います。

平均・分散・標準偏差の計算式
まず、計算式を見ておきます。
次に、次項の計算フォームで具体的な数値を使って、計算式に迫ります。
ここでは、標本を考慮しない分散を用います。
■平均
データ$${x}$$をデータ順$${( i )}$$に1番目から全部足して、データの個数$${n}$$で割って算出します。
$$
\begin{align*}
平均\ \bar{x}&=\cfrac{1}{n}\ (x_1+x_2+\cdots+x_n)\\
&=\cfrac{1}{n}\ \sum^n_{i=1}x_i
\end{align*}
$$
■分散
データ$${x}$$をデータ順$${( i )}$$に1番目から順に、まず、平均$${\bar{x}}$$を引いてから二乗して、この二乗した値を全部足して、最後にデータの個数$${n}$$で割って算出します。
ちなみに、1つ1つのデータと平均の差$${x_i-\bar{x}}$$のことを、偏差と呼びます。
分散は、1つ1つのデータと平均の差を取っていて、データが平均からどの程度散らばっているのかを示します。
$$
\begin{align*}
分散\ s^2&=\cfrac{1}{n}\ \{(x_1 -\bar{x})^2 +(x_2 -\bar{x})^2+\cdots+(x_n -\bar{x})^2 \}\\
&=\cfrac{1}{n}\ \sum^n_{i=1}(x_i-\bar{x})^2
\end{align*}
$$
■標準偏差
分散$${s^2}$$の平方根です。
標準偏差は分散と同様に、データの散らばり程度を示します。
分散は「二乗」したままなので、データの単位と合わないのですが、標準偏差は「二乗した分散の平方根」なので、データの単位と合います。
$$
標準偏差\ s = \sqrt{分散 s^2}
$$
x:国語の平均、分散、標準偏差
次の図は計算用のフォームです。

■平均
平均(c)は、x:国語データのID(i)1から10の合計(a)を、データ数(b)=10で割って算出します。
■分散
ステップ1:偏差(③)を求める
x:国語データのID(i)1から10について、平均(c)を差し引いて偏差(③)を算出します。
ステップ2:偏差の二乗(④)を求める
偏差(③)を二乗して偏差の二乗(④)を算出します。
ステップ3:偏差平方和(d)を求める
偏差の二乗(④)を合計して偏差平方和(d)を算出します。
ステップ4:分散(e)を求める
偏差平方和(d)をデータ数(b)で割って分散(e)を算出します。
■標準偏差
分散(e)の平方根が標準偏差(f)です。
y:英語の平均、分散、標準偏差
計算用フォームを掲載します。
計算の仕方はx:国語のときと同じです。
y:英語の方が平均値が大きく、標準偏差は小さいようです。

共分散と相関係数の計算式
x:国語とy:英語の変数単体の標準偏差が分かりました。
ここからは、xとyの2つの変数の関係式を確認します。
■共分散
データ$${x}$$と$${y}$$をデータペアの順$${( i )}$$に1番目から順に、まず、xの偏差($${x-平均\bar{x}}$$)とyの偏差($${y-平均\bar{y}}$$)を掛けます。掛けた値を全部足して(偏差積和)、最後にデータの個数$${n}$$で割って算出します。
$$
\begin{align*}
共分散\ s_{xy} &=\cfrac{1}{n}\ \{ (x_1-\bar{x})(y_1-\bar{y})+\cdots + (x_n-\bar{x})(y_n-\bar{y}) \}\\
&=\cfrac{1}{n}\ \sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})
\end{align*}
$$
■相関係数
共分散を「xの標準偏差 × yの標準偏差」で割ります。
相関係数の値は「$${-1~1}$$」となります。
$$
\begin{align*}
相関係数\ r&=\ \cfrac{xとyの共分散s_{xy}}{xの標準偏差s_x \times yの標準偏差s_y}\\
&=\cfrac{\cfrac{1}{n} \displaystyle\sum^n_{i=1}(x_i-\bar{x})(y_i-\bar{y})}{s_x s_y}\\
&=\cfrac{1}{n} \sum^n_{i=1} \cfrac{(x_i-\bar{x})}{s_x} \cfrac{ (y_i-\bar{y})}{s_y}\\
\end{align*}
$$
また、分散を用いると次のような計算式になります。
$$
相関係数\ r=\ \cfrac{xとyの共分散s_{xy}}{\sqrt{ xの分散s^2_x \times yの分散s^2_y}}\\
$$
x:国語とy:英語の共分散と相関係数
計算用フォームの全体像です。

左の【xとyの共分散の計算】が加わりました。
この部分をクローズアップします。

■共分散
ステップ1:偏差の積(④)を求める
データペアのID(i)1から10について、xの偏差(③)とyの偏差(③)を掛けて偏差の積(④)を算出します。
ステップ2:偏差積和(d)を求める
偏差の積(④)を合計して偏差積和(d)を算出します。
ステップ3:共分散(e)を求める
偏差積和(d)をデータ数(b)で割って共分散(e)を算出します。
■相関係数
共分散(e)を「xの標準偏差(f) × yの標準偏差(f)」で割ります。
ひとまずのまとめ
お疲れ様です!
ひとまずのサマリーです。
・xの平均と標準偏差: 54.5、18.29
・yの平均と標準偏差: 57.0、13.05
・xとyの共分散と相関係数: 154.10、0.6459
x:国語とy:英語の相関係数は約 0.64 。
xとyには中程度の正の相関がありそうです。
国語の得点が高くなると英語の得点が高くなる傾向がある、ということです。
散布図を確認しましょう。

右肩上がりの傾向が見られます。
散布図からも、x:国語の得点と、y:英語の得点に中程度の正の相関を確認できます。
さまざまな相関
相関を強くしてみる
ここからは素データを少しいじってみましょう。
xとyのデータの値は引き続き同じです。
ここでは、x:国語の得点とy:英語の得点を小さな順に並び替えています。
「x:国語の得点が低いほどy:英語の得点が低くなり、x:国語の得点が高いほどy:英語の得点が高くなる」データを作りました。

x:国語とy:英語の計算用フォームを見てみましょう。

データの値自体は変化していないので、平均・標準偏差も変わっていません。
ただし、xとyのペアの「偏差」の関係が変わったようです。
xとyの偏差の欄をご覧ください。
xもyも偏差の値の小さな順にデータが並んでいます。
「xとyのペア(同じID)の平均との乖離の傾向がまったく同じ」なんです!
このことは、共分散の計算で用いる「xとyの偏差積和」が変わることを意味しています。

偏差積和(d)が大きくなり、共分散(e)も大きくなりました。
共分散が大きくなると相関係数も大きくなります。0.9921です!
つまり、強い相関に向かうのです!
ひとまずのまとめ
xとyの全ペアで、x:国語の得点の高低とy:英語の得点の高低が一致するケースを見ました。
xとyのペアで、平均からの乖離の値(偏差)の順番が同じになったことで、xとyの偏差積和が最大化しました。
この結果、共分散の値も最大化し、相関係数が 0.99 という強い正の相関の値になりました。
散布図を見ましょう。

データ点が直線に張り付くように、一方向の傾向を表しています。
くっきりと強い正の相関が見られます。
相関関係を逆転してみる
今度は、「x:国語の得点が低いほどy:英語の得点が高くなり、x:国語の得点が高いほどy:英語の得点が低くなる」データで試してみましょう。

x:国語とy:英語の計算用フォームを見てみましょう。
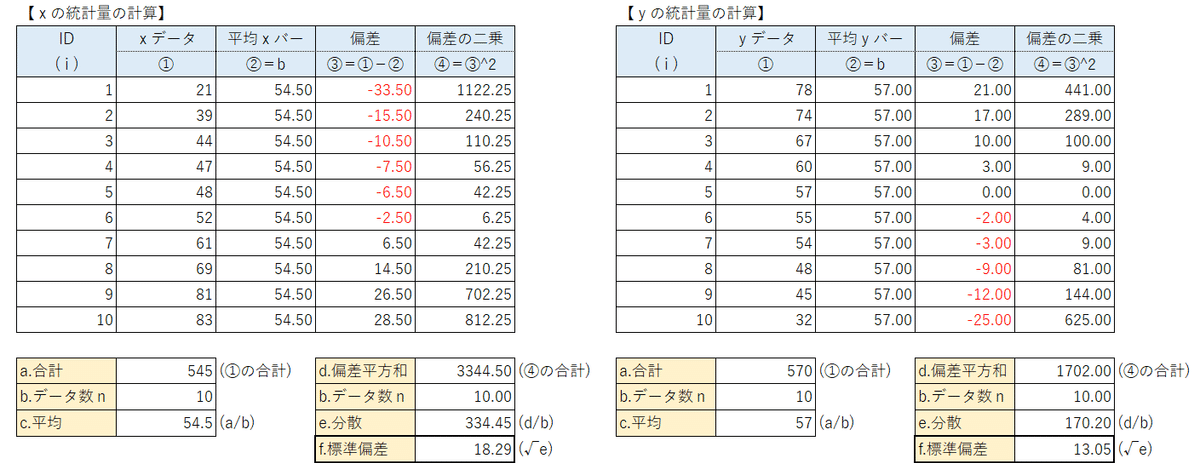
xは偏差の値の小さな順に並び、yは偏差の値の大きな順にデータが並んでいます。
「xとyのペア(同じID)の平均との乖離の傾向が真逆」なんです!
ペアで見ると、一方の値は「+」、もう一方の値は「-」になっています。
プラスマイナスも真逆です。
このことは、「xとyの偏差積和」に大きく影響します。
xとyの共分散の計算用フォームを見てみましょう。

xとyの偏差の積はほとんどマイナスです!
ペアで一方が「+」、もう一方が「-」の場合、掛けると「-」になるからです。
共分散もマイナスになるので、相関係数もマイナスです。
これが強い負の相関の正体です。
ひとまずのまとめ
xとyの全ペアで、x:国語の得点の高低とy:英語の得点の高低が真逆のケースを見ました。
xとyのペアで、平均からの乖離の値(偏差)の順番が全く逆になったことで、xとyの偏差積和がマイナス方向になり、最小化(絶対値は最大化)しました。
この結果、共分散の値がマイナス方向に最小化(絶対値は最大化)し、相関係数が -0.99 という強い負の相関の値になりました。
散布図を見ましょう。

くっきりと強い負の相関が見られます。
【極端な例】外れ値と相関係数
素データのID:10番のデータを 1000 にしてみました。
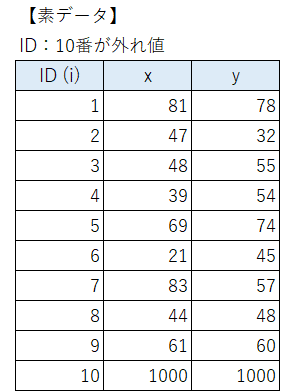
散布図は次のように10番の外れ値が影響して、直線的な関係が生まれてしまいました。飛び抜けています!

共分散は 8万超、相関係数は 0.9989 です。
ものすごく強い正の相関です。
ID:1~9番のデータは何も変わっていないので、10番の値「1000」だけの影響で、こんなに変わってしまいました。

このケースは極端です。
しかし、外れ値がある場合の相関係数や相関関係には注意が必要です。
次へ進みます
では、冒頭のデータ数300の「ランダムに生成した国語と英語の得点風の数値」データに進みましょうか。
いや、やめておきましょう。

実践する
共分散・相関係数を計算して散布図を描いてみよう
データ数を10個に減らした簡単なサンプルを用いて実践してみましょう。
CSVファイルのダウンロード
EXCEL・Python用に300個の方のCSVファイルを作成しました。
こちらのリンクからダウンロードできます。
データの項目名は相関係数の値を示しています。
たとえば「r090_x」は相関係数$${r=0.90}$$の$${x}$$の項目、「r090m_y」は相関係数$${r=-0.90}$$の$${y}$$の項目を示しています。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
電卓・手作業で作成してみよう!
「知る」の内容をもとにして、共分散と相関係数を手作業で計算して、散布図を作成しましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
データとグラフの関係も実感できると思います。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
共分散、相関係数の計算
「知る」の章の「共分散・相関係数の計算式」のとおりにEXCELで計算してみましょう。
また、EXCELの共分散と相関係数の関数を利用して計算してみましょう。
共分散は「COVARIANCE.P関数」、相関係数は「CORREL関数」で計算できます。一発ですね。
次の図は共分散の計算式「COVARIANCE.P関数」の設定例です。

EXCELサンプルファイルの概要
①「知る」の章で使用した「簡単なサンプルの計算用フォーム」を取り扱うのシートの全体像です。

②また、データ数300個の「ランダムに生成した国語と英語の得点風の数値」データを取り扱うシートもあります。
8つの散布図を描いています。

さまざまな相関を確認する
EXCELサンプルファイルのxデータ、yデータをさまざまな値に変えてみましょう。
サンプルデータは試験の得点のテイを醸すために、値を 0~100 点の範囲に収めていますが、この縛りを無くしてしまって、ガンガン数値を変えてみましょう。
ペアのデータの関係性を変化させることによって、共分散や相関係数の変化を確認できますし、散布図の形状の変化を味わうことができます。
バックアップを取っておけば、大胆に数字を変えても安心です。
データ数300のデータについては、データの変更と連動して、グラフのプロットが変わり、タイトルの相関係数の値も連動して変わります。
たくさん試してみてください。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、共分散・相関係数などの計算と、さまざまな相関係数の散布図の表示に取り組みます。
①ライブラリのインポート
主にpandasとnumpyを利用します。
回帰直線の作成にscikit-learnのLinearRegressionを使用します。
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile, index_col='ID')
print(df.shape)
display(df.head())
③x、yの統計量の表示1
numpyの以下の関数で統計量を取得します。
var: 分散
std: 標準偏差
cov: 共分散
corrcoef: 相関係数
# 分散、標準偏差、共分散、相関係数の計算
# 引数ddof=0とすることで母標準偏差等を計算。1/nで計算
# 引数ddof=1とすることで標本標準偏差等を計算。1/(n+1)で計算
# x軸のカラムとy軸のカラムを設定
x_cols = [df.columns[i] for i in range(0, 16, 2)]
y_cols = [df.columns[i] for i in range(1, 16, 2)]
# 分散・標準偏差の表示
print('【分散・標準偏差】')
for col in df.columns:
print(f'{col:16} 分散 : {np.var(df[col], ddof=0):7.2f}, '
f'標準偏差: {np.std(df[col], ddof=0):5.2f}')
# 共分散・相関係数の表示
print('\n【共分散・相関係数】')
for i, (x_col, y_col) in enumerate(zip(x_cols, y_cols)):
print(f'{x_col:7}と{y_col:7} 共分散: {np.cov(df[x_col], df[y_col])[0][1]:7.2f}, '
f'相関係数: {np.corrcoef(df[x_col], df[y_col])[0][1]:5.2f}')
【 f 文字列 】
分散・標準偏差・共分散・相関係数の計算は、print関数の「 f ' ' 」で囲まれた { } の中で行っています。
f文字列、フォーマット文字列と呼ばれるPythonの仕組みです。
f で開始して、シングルクォーテーション(' ')またはダブルクォーテーション(" ")で囲んだ文字列です。
f文字列の中に { } で関数を記述すると、print実行時に「関数の計算結果」を表示できます。
f 文字列の中の「分散 np.var()、標準偏差 np.std()、共分散 np.cov()、相関係数 np.corrcorf() 」を見つけてみましょう。
④相関係数のケースごとに散布図の表示
8つの散布図を表示します。
fig, ax = plt.subplots(2, 4, figsize=(9, 5), sharex=True, sharey=True)
for i, (x_col, y_col) in enumerate(zip(x_cols, y_cols)):
x, y = df[x_col], df[y_col]
corr_coef = np.corrcoef(x, y)
idx_row, idx_col = divmod(i, 4)
ax[idx_row][idx_col].scatter(x, y, s=0.7)
ax[idx_row][idx_col].set_xlim([0, 100])
ax[idx_row][idx_col].set_ylim([0, 100])
ax[idx_row][idx_col].set_title(f'$r={corr_coef[0][1]:.2f}$', fontsize=10)
fig.supxlabel('<--- 強い 相関の強さ 弱い --->')
fig.supylabel('<--- 負 相関の傾向 正 --->')
fig.suptitle('相関係数と散布図')
plt.tight_layout()
# plt.savefig('./scatter1.png') # グラフ画像ファイルの保存
plt.show()
散布図に回帰直線を追加します。
scikit-learnのLinearRegressionを使用します。
# 初期化
reg = LinearRegression()
result_dic = {}
# 描画
fig, ax = plt.subplots(2, 4, figsize=(9, 5), sharex=True, sharey=True)
for i, (x_col, y_col) in enumerate(zip(x_cols, y_cols)):
# 散布図のプロット
x, y = df[x_col], df[y_col]
corr_coef = np.corrcoef(x, y)
idx_row, idx_col = divmod(i, 4)
ax[idx_row][idx_col].scatter(x, y, s=0.7)
ax[idx_row][idx_col].set_xlim([0, 100])
ax[idx_row][idx_col].set_ylim([0, 100])
ax[idx_row][idx_col].set_title(f'$r={corr_coef[0][1]:.2f}$', fontsize=10)
# 回帰直線のプロット
x, y = df[[x_col]], df[[y_col]]
reg.fit(x, y)
y_pred = reg.predict(x)
ax[idx_row][idx_col].plot(x, y_pred, c='red', lw=0.5)
# 回帰直線の式と決定係数の表示
r2, coef, intercept = reg.score(x, y), reg.coef_[0][0], reg.intercept_[0]
result_dic[f'{corr_coef[0][1]:.2f}'] = {'r2': r2, 'coef': coef,
'intercept': intercept}
ax[idx_row][idx_col].text(5, 10, f'$y = {coef:.2f}x + {intercept:.2f}$', fontsize=7)
ax[idx_row][idx_col].text(5, 1, f'$R^2 = {r2:.2f}$', fontsize=7)
fig.supxlabel('<--- 強い 相関の強さ 弱い --->')
fig.supylabel('<--- 負 相関の傾向 正 --->')
fig.suptitle('相関係数と散布図')
plt.tight_layout()
# plt.savefig('./scatter2.png') # グラフ画像ファイルの保存
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
ネットには本当に助けていただいています。
「一定の相関係数になるように2系列の数字300個をランダムに生成する」
なにか方策はないだろうか?と、とにかく検索しました。
出会い1
最初に出会ったのは、PythonのOptunaを利用して、与えた相関係数になるように数値を生成するこの記事です。
Optunaによる最適化のコードが書かれていて、素晴らしいアイデア・知見を得ることができました。
ありがとうございます!
私のやりたいことにストレートな答えが見つかったかに思えました。
早速、データ生成に取り組みます。
相関係数 0.90 になるように、300個のデータを1000回の試行で最適化するのにかかった時間は2時間15分。
出来上がったデータの相関係数は 0.40 。
私の考えが甘かったのです。
出会い2
次に見つかった情報がこちらです。
今回利用したHADとの出会いです。
このツールは優れた統計処理機能を備えていて、2対のデータの「平均」と「分散共分散行列」を指定するだけで、瞬時に300個のデータセットが出来上がるのです!すごい。
生成データには小数点以下の値があります。時々100超の値が含まれます。
生成のやり直しと手作業のデータ補正は必要です。
しかし何よりも、瞬時にデータの素材が揃ったことが嬉しかったです!

HADは無料で「基礎的な分析から統計的検定,そして分散分析,回帰分析,一般化線形モデル,因子分析,構造方程式モデル,階層線形モデルなどの多変量解析が実行できる」そうです。
統計ツールをご検討の方、ぜひ使ってみてください。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
