9-1-2 一様性の適合度検定～同一期待度数の場合、分母は１つになるというお話

ネイピア DS

2023年9月23日 10:41

統計的仮説検定のトピック「適合度の検定」の２回目です。
適合度の検定の型を身につけてみませんか？

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解いて、知る・実践する

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
適合度検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

カイ二乗検定の分野　～適合度検定の分野
問2 一様性の適合度検定（曜日別の交通事故発生件数）

試験実施年月
統計検定2級 2018年11月問16（回答番号28）

📕公式テキスト：6.2 適合度の検定（203ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件に基づき、適合度の検定の「$${\chi^2}$$統計量が従う分布」と「帰無仮説を棄却できるかどうか」を解答します。

【条件】
・観測度数は以下の通り
　月曜:14、火曜:19、水曜:15、木曜:22、金曜:16、土曜:16
　合計＝標本サイズ102
・仮定する確率は、「どの曜日も発生率は同じ」である
・帰無仮説は「観測データは仮定する確率と一致する」
　（発生率は曜日に依存しない）
・有意水準$${5\%}$$で適合度検定を行う

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

条件より「適合度の検定」を行います。
適合度の検定は「片側検定（上側）」です。
仮定した確率「どの曜日も発生率は同じ」に基づいて期待度数を計算します。
観測度数と期待度数を用いて、検定統計量$${\chi^2}$$を計算します。
検定統計量$${\chi^2}$$が従う$${\chi^2}$$分布の自由度を計算します。
$${\chi^2}$$分布のパーセント点表より、有意水準$${5\%}$$のパーセント点を取得して、帰無仮説を棄却できるかどうか結論づけます。

この問題の統計的仮説検定の概要を図示します。

統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

手計算で検定

ステップ１：期待度数を計算する

期待度数は、理論的な確率や想定する確率といった「仮定する分布」の下でカウントされる度数です。

本問の仮定する分布は「全ての曜日は同じ確率」です。
表にすると全ての曜日が$${1/6 \fallingdotseq 0.1667}$$であることが分かります。

102件（標本サイズ）について、仮定する分布（全ての曜日は同じ確率）を用いて、期待度数を計算します。
全ての曜日の期待度数は一律$${102 \times 1/6=17}$$です

期待度数を表にしましょう。

次の計算で観測度数と期待度数を用いるので、両方の度数をまとめて掲載しましょう。

観測度数は曜日で凸凹がありますが、期待度数は平坦です。
棒グラフで観測度数と期待度数の違いを可視化しましょう。

グラフで比べると、観測度数と期待度数の間に大きな差は無いように見えます。
さて、適合度検定の結果はいかに・・・。

ステップ２：検定統計量$${\boldsymbol{\chi^2}}$$を計算する

カテゴリ（分類）ごとに「観測度数と期待度数の差の２乗」を「期待度数で割り」、全カテゴリを合計します。

本問のカテゴリは曜日「月」から「土」までの６つです。
検定統計量$${\chi^2}$$は次の計算式を用いて計算します。

先程まとめた観測度数と期待度数の値を当てはめて、検定統計量$${\chi^2}$$を計算しましょう。

分母の期待度数はすべて$${17}$$になります。
計算途中で割り算せずに、分子を計算して合計しましょう。
差の二乗の箇所は必ず正の数になります。
サザンが９、ニニンが４が２回、ゴゴ２５，インイチが１が２回、という具合に、暗算しやすいです。

検定統計量の計算で得られた$${\chi^2}$$値は$${2.59}$$です。

ステップ３：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の自由度

観測度数が１変数の場合、検定統計量$${\chi^2}$$は自由度$${k-1-\alpha}$$の$${\chi^2}$$分布に従います。
$${k}$$はカテゴリの数です。
$${\alpha}$$は観測データから推定する分布のパラメータの数（補足参照）です。
本問で取り扱う観測度数は「事故が発生した曜日」の１変数であり、カテゴリの数は６（月～土の６つ）、データから推定するパラメータの数は０ですので、自由度は$${k-1-\alpha=6-1-0=5}$$です。

解答選択肢（ア）は「自由度$${5}$$の$${\chi^2}$$分布」です。

【補足】データから推定するパラメータの数

大半の統計検定２級の問題では、「データから推定するパラメータの数」を意識する必要はありません。
自由度は「カテゴリの数－１」で求めます。

ただし、仮定する分布にポアソン分布を想定する問題では注意が必要です。
観測データからポアソン分布の平均パラメータ$${\lambda}$$の推定値$${\hat{\lambda}}$$を求めて、期待度数を計算するケースがあります。
この場合、観測データから分布のパラメータを１つ推定しているので、$${\chi^2}$$分布の自由度は$${k-1\boldsymbol{-1}}$$のように、推定パラメータ個数を最後に差し引きします。

ステップ４：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の上側パーセント点

続いて上側パーセント点を取得して棄却域を確認します。
ここで重要なお知らせ。

【重要ポイント】
・適合度検定は片側・上側検定です。

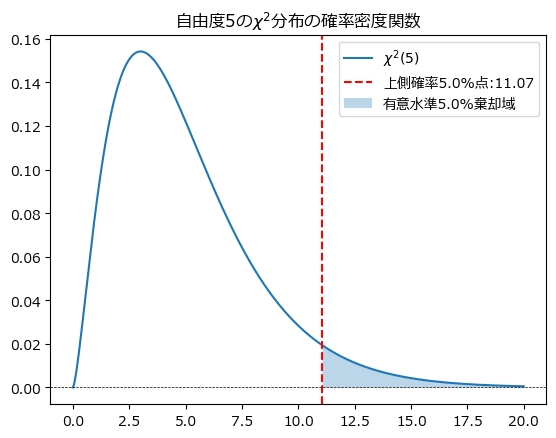
適合度検定は片側・上側検定ですので、有意水準$${5\%}$$の棄却域を求める際には、自由度$${5}$$の$${\chi^2}$$分布のパーセント点表より上側確率$${5\%}$$点を取得します。

自由度$${5}$$の上側確率$${5\%}$$点は$${11.07}$$です。

$${\chi^2}$$分布の確率密度関数をグラフで確認しましょう。

ステップ５：結論を出す

$${\chi^2}$$値$${=2.59}$$と上側確率$${5\%}$$点$${=11.07}$$を比べます。
$${\chi^2}$$値は上側確率$${5\%}$$点より小さいため、棄却域から外れています。
よって、帰無仮説は棄却されません。

解答選択肢（イ）は「棄却しない」です。

最後にグラフで棄却域と$${\chi^2}$$値の関係を確認しましょう。

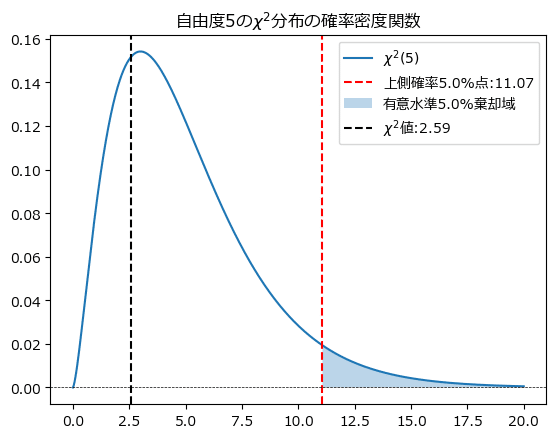
$${\chi^2}$$値は棄却域から大幅に外れています。
おそらく$${p}$$値は大きな値でしょう。

手計算は以上となります。

EXCELで検定

計算シートを用いて適合度検定を行います。

計算シートの全体像
左側の表には、観測度数と仮定する分布（確率）を登録します。
期待度数を計算して、観測度数・期待度数の両方を整えます。
また、カテゴリごとに$${(観測度数-期待度数)^2/期待度数}$$の計算を行って合計を取り、$${\chi^2}$$値にしています。
右側の入力パラメータは「有意水準」です。

観測度数・期待度数・有意水準より、$${\chi^2}$$値、上側確率％点、$${p}$$値を求めて、判定します。

適合度検定の実行

上記の計算シートには既に必要なデータ、パラメータを設定済みです。
計算値によると、自由度は$${5}$$、$${\chi^2}$$値は$${2.588}$$、上側確率$${5\%}$$点は$${11.07}$$です。
$${\chi^2}$$値が上側確率5%点よりも小さいので、帰無仮説は棄却できません。

解答選択肢は（ア）自由度$${5}$$の$${\chi^2}$$分布、（イ）棄却しない、です。

EXCELの関数

EXCELの CHISQ.TEST 関数を用いて、適合度検定の$${p}$$値を算出できます。
引数は、CHISQ.TEST ( 観測度数のデータ範囲, 期待度数のデータ範囲 ) です。
シンプルなのでぜひ使ってみてください！

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで検定

scipy.stats の chisquare を用いて適合度検定を実行します。

①インポート

### インポート
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②データとパラメータの設定
問題で与えられた「観測度数」、「仮定する確率」、「有意水準」を設定します。
この３つの情報から、期待度数、自由度、上側確率$${5\%}$$点を算出します。
$${\chi^2}$$分布の上側確率$${5\%}$$点の取得には、scipy.stats の chi2.isf を利用しました。

### データとパラメータの設定

## 設定
# 観測度数 : 月～土の順
observed_freq = np.array([14, 19, 15, 22, 16, 16])
# 仮定する確率 : 一律1/6
expected_prob = np.repeat(1/observed_freq.shape[0], observed_freq.shape[0])
# 有意水準
alpha = 0.05

## 検定に利用する値の計算（設定）
# 期待度数
excepted_freq = expected_prob * observed_freq.sum()
# 自由度
df = observed_freq.shape[0] - 1
# 有効水準のカイ二乗分布の上側パーセント点
critical_value = stats.chi2.isf(alpha, df)

## 観測度数と期待度数の表示
summary_table = pd.DataFrame(
                  data={'観測度数': observed_freq,
                        '期待度数': excepted_freq},
                  index=['月', '火', '水', '木', '金', '土']).T
display(summary_table)

③適合度検定の実施
scipy.stats の chisquare を用いて適合度検定を行います。
引数は、chisquare ( 観測度数データ, 期待度数データ ) です。
戻り値は、$${\chi^2}$$値と$${p}$$値です。

### 適合度検定の実施
chi2_value, p_value = stats.chisquare(observed_freq, excepted_freq)
print(f'chi2_value:{chi2_value:.3f}, p_value:{p_value:.3f}')

出力イメージ

（予告）
$${p}$$値が$${0.763}$$と大きな値なので、きっと帰無仮説を棄却できないでしょう。

④結論の表示
有意水準と$${p}$$値を比較して、帰無仮説を棄却できるかどうかを判定します。

### 結論の表示
if p_value < alpha:  # p値が有意水準より小さい場合：棄却できる
    result = ('棄却される', '言える')
else:                # p値が有意水準以上の場合：棄却できない
    result = ('棄却されない', '言えない')
print(f'結論\n有意水準{alpha:.1%}で帰無仮説は{result[0]}\n'
      f'対立仮説「観測データは仮定する確率分布に一致しない」と{result[1]}')

### 統計量の表示
print('\n統計量')
print(f'自由度{df}のカイ二乗分布の上側{alpha:.1%}点:{critical_value:.3f}, '
      f'カイ二乗値:{chi2_value:.3f}')
print(f'有意水準{alpha:.3f}, p値:{p_value:.3f}')

やはり帰無仮説を棄却できませんでした。

解答選択肢は（ア）自由度$${5}$$の$${\chi^2}$$分布、（イ）棄却しない、です。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

以上で終了です。
お疲れ様でした。

解答

③ です。

難易度　やさしい

・知識：適合度の検定、$${\chi^2}$$分布のパーセント点表
・計算力：数式組み立て（低）、電卓（中）
・時間目安：2分

おわりに

この記事は前回記事の適合度検定の構成、パーツをそっくり転用して作成しました。
お気づきでしょうか？
適合度検定の要点を押さえて、答案作成の流れを会得できれば、あとは同様のスタイル＝型どおりの所作で解答すればよいのです。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

いいなと思ったら応援しよう！

この記事が参加している募集

#沼落ちnote

9,652件

9-1-2 一様性の適合度検定 ～ 同一期待度数の場合、分母は１つになるというお話

問題を解いて、知る・実践する

手計算で検定

EXCELで検定

Pythonで検定

おわりに

のんびり統計シリーズの記事

いいなと思ったら応援しよう！

この記事が参加している募集

9-1-2 一様性の適合度検定～同一期待度数の場合、分母は１つになるというお話