
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第2章2.4「プログラミングの基礎」
第2章「プログラミングの基礎」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第2章「プログラミングの基礎」2.4節「プログラミングの基礎」および2.5節「演習問題」の Python写経活動 を取り扱います。
前前回からの3記事はシミュレーションの準備体操にあたります。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いて準備体操の旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.4 プログラミングの基礎
テキストはシミュレーションの基礎になる「Rによるプログラミング」に慣れることを目標にして、初歩的なコードを R で書いています。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回取り組む R のコード・構文は Python とよく似ています。
直近で利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# 描画
import matplotlib.pyplot as plt
2.4.1 反復
■ for 文の最初の一歩
for 文、while 文に慣れましょう。
どちらも「同じ処理を繰り返し実施」するときに使います。
テキストの最初の for 文体験は、1 から 3 までの数字を画面に表示することです。
for により、1 から 3 までの範囲の数値(range(1, 4))を1つずつ繰り返し取り出して、変数「i」に設定し、字下げ(インデント)された処理(print(i))を実行します。
### 38ページ for文
for i in range(1, 4): # 1から3までの整数
print(i) 【実行結果】
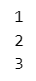
【Pythonの注意事項】
範囲の終点は3なのですが、Pythonの文法上、終点+1を指定する必要があり、「range(1, 4)」となります。
「1」から「4の1つ前=3」までの整数値を得られます。
■ リスト内の数値の総和計算
リスト x の数値$${3, 5, 1}$$の総和を計算します(合計します)。
for 文では、リスト x からスライスで値を1つずつ取り出して、変数 y に加算しています。
「y = 0」はひとまず、おまじないだと思っておきましょう。
### 38ページ 総和
x = [3, 5, 1] # リスト型を使用
y = 0
for i in range(len(x)): # iは0から2までの整数値。リストxの長さlenは3(0から2まで)
y = y + x[i] # xからスライス(インデックス指定)で値を取り出しyと足し算
print(y)【実行結果】
合計は9です。
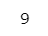
ちなみにsum関数を使うと簡単に合計を計算できます。
### sum関数
sum(x)【実行結果】
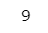
■ リストから直接値を取る for 文
1つ上の range を用いた for 文の変数 i には$${0, 1, 2}$$と0から順番に値が設定されました。
ここでは、リストの値を変数 i に設定する方法で for 文を作成します。
### 39ページ 総和
y = 0
for i in [1, 3, 5, 3, 6, 2]:
print(i)
y = y + i【実行結果】
変数 i にはリストの先頭から順番に値$${1, 3, 5, 3, 6, 2}$$が取り出されました。
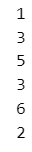
総和を持っている変数 y を表示します。
print(y)【実行結果】
しっかり合計できています。
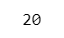
■ 数列を作成
1から20の範囲で4つずつ等間隔で数列を作成します。
リストを使うバージョンです。
### 40ページ 1から20まで4ずつ間隔を開けた数列をつくる
list(range(1, 21, 4)) # リスト型を利用【実行結果】
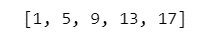
numpy配列を使うバージョンです。
np.arange() を使用します。
# numpy配列を利用する場合、arangeを使用
np.arange(1, 21, 4)【実行結果】
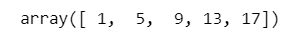
range() は整数のみ扱えますが、np.arange() は整数と小数(小数点の付いた数値)を扱えます。
■ 決して実行しないでください、の for 文
以下の内容の R コードは for 文が止まらない「永久ループ」になるようです。
安心してください、Pythonは止まりますよ!
### 40ページ 決して実行しないでください はpythonでは止まるので安心
for i in range(1, 6):
print(i)
i = 3【実行結果】
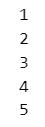
■ for 文の入れ子
変数 i を用いる for 文の内側に、変数 j を用いる for 文があります。
内側の for 文が細かに回されます。
### 41ページ 文字列をつなげる
for i in range(1, 6):
for j in range(3, 6):
# f文字列で数値と文字を混在した文字列を作成。{}の中に変数を設定する
print(f'{i} + {j} = {i + j}')【実行結果】
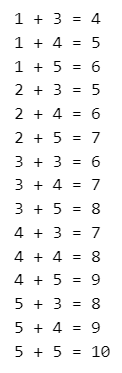
■ 行列積を for 文で計算
テキストにならって行列の積を numpy で計算します。
numpy配列で見立てた行列$${A,B}$$をドット積「@」で計算します。
### 42ページ 行列積 numpy配列を利用
# 行列A, Bの作成
A = np.arange(1, 7).reshape((2, 3), order='F')
B = np.arange(1, 13).reshape((3, 4), order='F')
# 行列A, Bの表示
print(A)
print(B)
# 行列積の計算
print(A @ B)【実行結果】

この行列積の計算を for 文の入れ子を用いた足し算で行います。
### 43ページ 総和で行列積を実装
C = np.zeros((2, 4))
for i in range(A.shape[0]):
for j in range(B.shape[1]):
for k in range(A.shape[1]):
C[i, j] = C[i, j] + A[i, k] * B[k, j]
print(C)【実行結果】
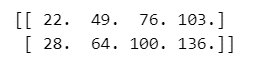
■ もう1つの反復法、while
for 文は range() やリストなどで与えた値群に対して繰り返し処理します。
一方、while 文は評価が「True」の間、繰り返しを続けます。
次のコードでは、a が 20 未満の間(a < 20 が True 評価)、a に 3 を加算しています。
### 43ページ while
a = 0
while a < 20:
a = a + 3
print(a)【実行結果】
a が 21 になった時点で、20以上(つまり、a < 20 がFalse)になり、繰り返し処理が終了しています。
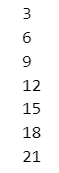
while 文の処理中に「brake」が入ると、繰り返し処理を完了します。
### 44ページ break
a = 0
while a < 20:
a = a + 3
print(a)
break【実行結果】
1回めの while ループで break が発動されました。
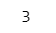

2.4.2 条件分岐
if 文に取り組みます。
以下は大雑把な構文です。
if 条件1: # 条件1がTrueの場合
処理
elef 条件2: # 条件1がFalse、条件2がTrueの場合
処理
else: # 条件1も条件2もFalseの場合
処理■ if 文、最初の一歩
もしも変数 a が 10 超の場合、「a > 10」と表示するコードです。
### 45ページ 条件分岐
a = 9
if a > 10:
print('a > 10')【実行結果】
何も表示されません。
変数 a が 9 なので、if 文の条件「変数 a が 10 超」に該当せず、「print('a > 10')」の処理が飛ばされました。
■ if ~ else
変数 a が 10 超の場合に「a > 10」と表示し、それ以外(else)の場合に「a <= 10」と表示するコードです。
### 45ページ 条件分岐2
if a > 10:
print('a > 10')
else:
print('a <= 10')【実行結果】
a は 10 超ではないので、else の処理が実行されて「a <= 10」と表示されました。
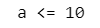
■ ifelse 関数に似た書き方
1行で if ~ else を表現してみます。
「if が True のときの処理」 if 条件 else 「if がFalseのときの処理」のような書き順です。
### 46ページ ifelse関数に似た1行if文の書き方
print('a > 10') if a > 10 else print('a <= 10')【実行結果】
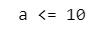
■ if ~ elif ~ else
条件が複数ケースある場合、2つめの if は「elif」と書きます。
### 46ページ if~else if~else
if a > 10:
print('a > 10')
elif a > 8:
print('8 < a <= 10')
else:
print('a <= 8')【実行結果】
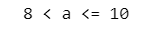

論理式の書き方
if 文の条件に用いる「論理式」の例です。
■ 等しい、等しくない
等しい:「==」、等しくない「!=」です。
### 47ページ 基本形
if a == 9:
print('a は 9 に等しい')
if a != 9:
print('a は 9 ではない')【実行結果】
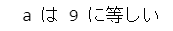
■ かつ
複数の条件が「かつ」(すべて満たされる)で評価する場合、条件を「and」か「&」で繋げます。
### 47ページ 論理積 and または &
b = 10
if a < 10 and b <= 10:
print('a は 10 より小さく、b は 10 以下である')【実行結果】
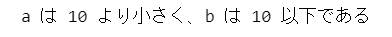
if a < 10 & b <= 10:
print('a は 10 より小さく、b は 10 以下である')【実行結果】
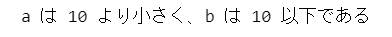
■ または
複数の条件が「または」(どれかに該当する)で評価する場合、条件を「or」か「|」で繋げます。
### 47ページ 論理和 or または |
b = 10
if a > 10 or b < 10:
print('a は 10 より大きいか、b が 10 より小さい')
else:
print('a が 10 以下か、b が 10 以上')【実行結果】
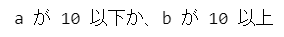
if a > 10 | b < 10:
print('a は 10 より大きいか、b が 10 より小さい')
else:
print('a が 10 以下か、b が 10 以上')【実行結果】
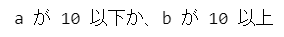
■ 配列の論理判断
複数の要素を持つnumpy配列の論理判断の例です。
要素が1から6の整数 numpy配列$${A}$$(ベクトル相当)の中から3に合致するかどうかの論理判断を行います。
### 48ページ ベクトルの論理判断 numpy配列を利用
A = np.arange(1, 7)
A == 3【実行結果】
3番めの要素「3」が True、その他の要素は False です。

上記の論理式をそのまま if 文の条件に使うと、エラーになります。
### 48ページ エラーになるif文
if A == 3:
print('3がありました')【実行結果】
どの要素で True か False かを判断するのか特定できないのでエラーになるようです。

たとえば次のような条件にすると、変数$${A}$$に3が含まれる場合に「3がありました」と表示できます。
any() は A == 3 の中に1つ以上の True がある場合に、True を返します。
### エラーにならないif文
if any(A == 3):
print('3がありました')■ FuzzBuzz問題
テキストにならってFuzzBuzz問題のコードを書きます。
1~15の数字を順番にコールしますが、3で割り切れる場合は「Fizz」、5で割り切れる場合は「Buzz」、3と5で割り切れる場合は「FizzBuzz」とコールするようです。
### 49~50ページ 最終形
for i in range(1, 16):
if i % 3 == 0 and i % 5 == 0:
print('FizzBuzz')
elif i % 3 == 0:
print('Fizz')
elif i % 5 == 0:
print('Buzz')
else:
print(i)【実行結果】
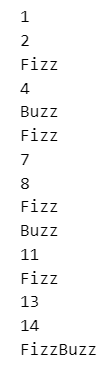
テキストの別解の Python コードです。
### 51ページ 別解
for i in range(1, 16):
msg = ''
if i % 3 == 0:
msg = 'Fizz'
if i % 5 == 0:
msg = msg + 'Buzz'
print(i, ':', msg)【実行結果】


2.4.3 記述統計関数を作ってみよう
テキストにならって記述統計関数を作成します。
■ 標本分散を算出する関数
R には(憶測ですが)標本分散を算出する関数が無いのでしょうか?
テキストでは標本分散算出関数 var_p を作成して、後続の章で活用します。
### 52ページ 標本分散s²を算出する関数の定義
def var_p(x): # xはnumpy配列
n = len(x)
mean_x = x.mean()
var_x = sum((x - mean_x)**2) / n
return var_x別バージョンです。
### 53ページ 標本分散s²を算出する関数の定義2 不偏分散を利用
def var_p2(x): # xはnumpy配列
n = len(x)
var_x = x.var(ddof=1) * (n - 1) / n # var(ddof=1)で不偏分散を算出
return var_xPython では numpy の var 関数で不偏分散、標本分散を使い分けて計算できます。
自由度から差し引く数を ddof 引数で指定します。
不偏分散を計算する場合は、ddof = 1、標本分散を計算する場合は、ddof = 0 です。
2つの関数とnumpyのvar関数で標本分散を計算してみます。
### 関数を試す
x = np.array([7, 5, 9, 10, 8])
print('var_p(x) :', var_p(x))
print('var_p2(x):', var_p2(x))
print('numpy.var:', x.var(ddof=0))【実行結果】
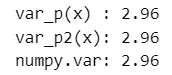

コラム:コード規約
テキストは「コードの見やすさ(可読性の高さ)」を意識しよう!と提案しています。
Python ではコードスタイルを PEP8 などで定義・提案しています。
■ 変数名 Camel Case, Snake Case
### 54ページ 変数名 Camel Case, Snake Case
ObjectName = 2 # PythonではCamel Caseを主にクラス名に利用
object_name = 2 # Pythonで一般に用いられる記法。先頭は小文字■ インデントのない表記
テキストはインデントのない表記は読みにくくなるので避けましょう、と提案しています。
インデントのない表記の例です。
### 54ページ インデントのない表記
from itertools import product
for i, j in product(range(1, 6), range(3, 11)): print(i, '+', j, '=', i + j)【実行結果】
途中の一部の表記を省略しています。
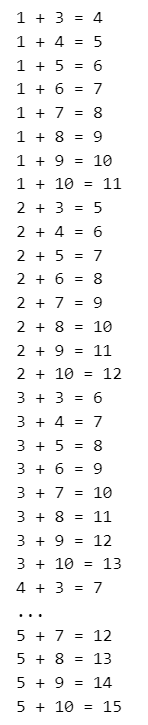
インデントのある表記に変更します。
### 54ページ インデントのある表記
for i in range(1, 6):
for j in range(3, 11):
print(i, '+', j, '=', i + j)【実行結果】上の実行結果と同じ
なお、上記例の計算結果だけを変数に格納する場合、Python ではリスト内包表記を使うことがあります。
### リスト内包表記
result = [i + j for i in range(1, 6) for j in range(3, 11)]
print(result)【実行結果】
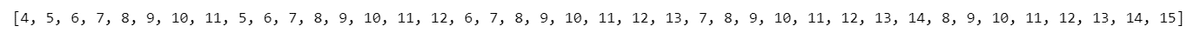

コラム:実行時間
テキストはコードの書き方次第でコンピュータの処理時間が変わることを示しています。
特に for 文などで大量の繰り返し処理を実行する場合、処理時間の違いが明確になります。
この記事では Jupyter Notebook で「%time」または「%%time」と記述して、CPU times(コンピュータのCPUを使用した時間)とWall times(全処理時間)を計測します。
■ 平均値の計算
要素数$${10}$$と要素数$${10^7}$$の平均値の処理時間を比べます。
### 56ページ 1~10の平均値
x = list(range(1, 11))
%time np.mean(x)【実行結果】
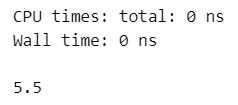
### 56ページ 1~10^7の平均値
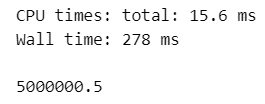
x = list(range(1, 10**7 + 1))
%time np.mean(x)【実行結果】
処理時間の単位がミリ秒なので体感時間は短いかもですが、10までの平均値計算よりも桁が100000違うことになります。
■ 配列の要素追加か、初めに要素数の器を作るか
テキストは100000回の計算値を配列(変数)に格納する際、予め器を作っておいたほうが処理時間が短くなる実験をします。
実験パターンは次の3つ。
① 計算の都度、配列に要素を追加
② 計算開始前に100000個のゼロ要素(器)を作ってから計算値を格納
③ 計算開始前に100000個のNaN要素(器)を作ってから計算値を格納
%%time
### 56ページ 要素追加方式
## 最初は1だけ持っている配列
x = np.array([1], dtype='int64')
## 反復回数
iter = 100000
## i番目の要素はi-1番目の要素にiを足したもの
for i in range(1, iter):
x = np.append(x, x[i-1] + i)【実行結果】
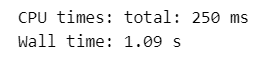
%%time
### 57ページ ゼロ事前用意方式
## 反復回数
iter = 100000
## 最初に0が入った配列を用意
x = np.zeros(iter)
## 最初の要素に1を代入
x[0] = 1
## i番目の要素はi-1番目の要素にiを足したもの
for i in range(1, iter):
x[i] = x[i-1] + i【実行結果】
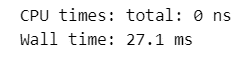
%%time
### 57ページ NaN事前用意方式
## 反復回数
iter = 100000
## 最初にNaNが入った配列を用意
x = np.repeat(np.nan, repeats=200000)
## 最初の要素に1を代入
x[0] = 1
## i番目の要素はi-1番目の要素にiを足したもの
for i in range(1, iter):
x[i] = x[i-1] + i
## 不要なNaNを削除
x = x[~np.isnan(x)]【実行結果】
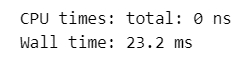
③の予めNaN要素で器を作っておく方法が最も処理時間が短くなりました。
2.5 演習問題
テキストの3つの演習問題を Python で解きます。
解答コードとその実行結果のみ記載します。
2.5.1 演習問題1
### 58ページ 2.5.1 演習問題1:1から100までの偶数を合計
sum((range(0, 101, 2)))【実行結果】
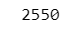
2.5.2 演習問題2
### 58ページ 2.5.2 演習問題2:1からxまでの偶数を合計する関数
def sum_even_number(x):
return sum(range(0, x+1, 2))### 実行
print(sum_even_number(100))
print(sum_even_number(1000))【実行結果】
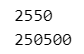
2.5.3 演習問題3
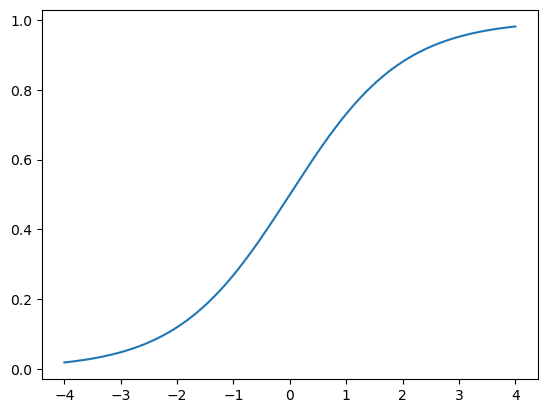
### 59ページ 2.5.3 演習問題:ロジスティック関数(シグモイド関数)
# ロジスティック関数の定義
def logistic(x):
return 1 / (1 + np.exp(-x))
# -4から4までのx軸の値の設定
xval = np.linspace(-4, 4, 1001)
# ロジスティック関数曲線の描画
plt.plot(xval, logistic(xval));【実行結果】
今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
