
「回帰分析から学ぶ計量経済学」をPythonで写経 ~ 第4章「変数の工夫」①ダミー変数・コンジョイント分析
第4章「変数の工夫」
書籍の著者 山澤成康 先生
この記事は、書籍「回帰分析から学ぶ計量経済学」第4章「変数の工夫」の Python写経活動 を取り扱います。
今回は「ダミー変数」を堪能します!
時系列分析を彩る、水準変化ダミー、季節ダミー、トレンド変数を扱い、ダミー変数を説明変数に用いる分析手法の1つ、コンジョイント分析に取り組みます!
では書籍を開いて回帰分析の旅に出発です🚀

はじめに
書籍「回帰分析から学ぶ計量経済学」のご紹介
このシリーズは書籍「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」(オーム社、「テキスト」と呼びます)の Python 写経です。
テキストは、2023年11月に発売され、副題「Excelで読み解く経済のしくみ」のとおり、主に Excel を用いて、計量経済学を平易に学べる素晴らしい書籍です。
テキストの「はじめに」に著者の先生が執筆の動機を書かれています。
社会人の統計リテラシーの向上をテーマの1つとした科研費プロジェクトの最終年度で、広く社会人に向けてわかりやすい経済分析の本を書きたかったのです。
私にとって計量経済学は高嶺の花ですが、このテキストでさまざまな回帰分析のアプローチを知ることができました。
また、書籍の Excel 処理を Python に置き換える「寄り道写経」の実践を通じて、回帰分析のお気持ちに少し近づけた感じがいたします。
回帰分析に慣れ親しむのに丁度良いレベル感と内容ですので、これはぜひともブログにしたい!と思って現在に至ります。
計量経済学の色を薄め、データ分析の色を濃いめに書いてまいります!

引用表記
この記事は、出典に記載の書籍に掲載された文章と配布データを引用し、適宜、掲載文章・配布データを改変して書いています。
【出典】
「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」
第1版第1刷、著者 山澤成康、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
第4章 変数の工夫
この記事は第4章の以下の節を取り扱います。
4.2 ダミー変数とは(4.1 変数をどう選ぶかを含みます)
4.3 コンジョイント分析
記事に用いるデータは、オーム社の書籍紹介サイトからダウンロードできる Excel ファイル内のデータをもとにしてCSVファイルを作成し、data フォルダに格納しています。
第4章で用いるライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 統計処理
import scipy.stats as stats
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.api import het_white # ホワイトの検定
from statsmodels.stats.outliers_influence import variance_inflation_factor # VIF
import lmdiag # 残差プロット
# 描画
import matplotlib.pyplot as plt
from matplotlib.ticker import PercentFormatter # 軸目盛りを%表示
import seaborn as sns
import japanize_matplotlib
# ワーニング非表示
import warnings
warnings.simplefilter('ignore')
4.2 ダミー変数とは
■ 例題:冷夏ダミー p.122
テキストによると「ダミー変数は0と1だけで作った、人工の変数のこと」であり、「一時点だけ異常値があったり、ある時点以降に制度変更があったりする場合に使います」とのことです。
一時点だけ異常値がある場合の例として、テキストは「冷夏による水稲の収穫量の減少」をダミー変数で表現する例題を出しています。

2000年から2021年の水稲の作付面積と収穫量データを読み込みます。
2003年だけが「冷夏」であり、冷夏ダミー変数の値を$${1}$$にしています。
### データの読み込み
# 収穫量: 1000t, 作付面積: 1000ha
# CSVファイルの読み込み
df1 = pd.read_csv('./data/04_01_rice.csv', index_col=0)
# インデックスを数字に変換
df1.index = range(2000, 2000 + len(df1))
df1.index.name = '年'
# 冷夏ダミー変数(2003年のみ1、その他の年は0)の追加
df1['冷夏ダミー'] = np.where(df1.index==2003, 1, 0)
# データフレームの表示
print('df1.shape:', df1.shape)
display(df1.head())【実行結果】

散布図でデータを確認しましょう。
### 散布図の描画
# 回帰直線付き散布図の描画
sns.lmplot(data=df1, x='作付面積', y='収穫量', ci=None, height=4, aspect=1.4,
hue='冷夏ダミー', palette=['tab:blue', 'tab:red'],
line_kws={'color': 'tomato'},)
# 年のテキストの表示
for year in df1.index:
# フォントサイズの設定 冷夏ダミー==1(2003年): 14, その他: 6
fontsize = 14 if df1.loc[year, '冷夏ダミー'] == 1 else 6
# データ点の傍に年を表示
plt.annotate(text=year,
xy=(df1.loc[year, '作付面積']+5, df1.loc[year, '収穫量']+10),
fontsize=fontsize)
# 修飾
plt.xlabel('作付面積 [1000ha]')
plt.ylabel('収穫量 [1000t]')
plt.title('水稲の作付面積と収穫量')
plt.grid(lw=0.5)
plt.show()【実行結果】
通常の年は概ね回帰直線(朱色の斜線)に沿っていますが、2003年は回帰直線から外れていて(外れ値!)、収穫量が減少している様子を確認できました。
なおこの回帰直線は外れ値の影響を受けています。

続いて、冷夏ダミーを説明変数に加えた次の式を用いて、回帰分析を実行します。
$$
収穫量 = \beta_1 \times 作付面積 + \beta_2 \times 冷夏ダミー + 切片
$$
statsmodels の ols(formula.api)を利用します。
### ダミー変数を用いた回帰の実行
result = smf.ols(formula='収穫量 ~ 作付面積 + 冷夏ダミー', data=df1).fit()
display(result.summary())【実行結果】
冷夏でおよそ$${1000}$$トン減少すると推定されました。

回帰式による予測値を可視化しましょう。
### 散布図の描画
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 回帰直線付き散布図の描画
sns.regplot(data=df1, x='作付面積', y='収穫量', color='tab:blue', ci=None,
line_kws={'color': 'royalblue', 'ls': '--', 'lw': 1},
scatter_kws={'alpha': 0.5, 's': 70},
label='実測値', ax=ax)
# 収穫量の予測値の描画
ax.scatter(df1['作付面積'], result.fittedvalues, fc='None', ec='tab:red', lw=1.5,
s=80, label='予測値')
# 収穫量の予測値(冷夏を除く)に基づく回帰直線の描画
drop_outlier = result.fittedvalues.copy()
drop_outlier.loc[2003] = np.nan
ax.plot(df1['作付面積'], drop_outlier, color='tomato', ls='--', lw=2,
label='予測値の回帰直線')
# 修飾
plt.xlabel('作付面積 [1000ha]')
plt.ylabel('収穫量 [1000t]')
plt.title('水稲の作付面積と収穫量~冷夏ダミーで推定')
plt.grid(lw=0.5)
plt.legend()
plt.show()【実行結果】
赤い丸は予測値、赤い点線は予測値の回帰直線、青い点線は冷夏ダミーを考慮しない回帰直線です。

2003年(冷夏)の予測値は実測値にピタリと当てはまっています。
2つの回帰直線を比べると、予測値(赤い点線)の傾きが大きくなっています。
予測値の回帰直線の傾きは、2003年の外れ値の影響を除外していると考えられます。

■ 傾きが途中で変わる場合(構造変化、係数ダミー) p.124
テキストは経済成長の傾向が大きく変化した「バブル経済終焉」を「構造変化」の題材にして、実質GDPのトレンドを推定しています。
1955~2021年度の実質GDPデータを読み込みます。
### データの読み込み
# 実質GDP: 兆円
# CSVファイルの読み込み
df2 = pd.read_csv('./data/04_02_gdp.csv', index_col=0)
# トレンド項を追加
df2['トレンド'] = np.arange(1, len(df2)+1)
# 構造変化ダミーを追加 1990年に構造変化があったと想定
df2['構造変化ダミー'] = np.where(df2.index >= 1990, 1, 0)
# データフレームの表示
print('df2.shape:', df2.shape)
display(df2)【実行結果】
トレンドは1955年(始点)を$${1}$$にして、毎期$${+1}$$カウントアップしています。
構造変化ダミーは、1989年までは$${0}$$、1990年からは$${1}$$を設定しています。
1990年に構造変化=バブル経済終焉による経済成長の変化が起きて、以後、構造変化が継続している、との見立てです。

次の式を用いて、回帰分析を実行します。
$$
\begin{align*}
実質GDP =\ &\beta_1 \times トレンド + \beta_2 \times 構造変化ダミー \\
&+ \beta_3 \times トレンド \times 構造変化ダミー + 切片
\end{align*}
$$
構造変化前は構造変化ダミー$${=0}$$ですので、式は以下のような感じになります。
$$
実質GDP = \beta_1 \times トレンド + 切片
$$
構造変化後は構造変化ダミー$${=1}$$ですので、式は以下のような感じになります。
$$
実質GDP = (\beta_1 + \beta_3) \times トレンド + (\beta_2 + 切片)
$$
構造変化ダミーの係数は、$${\beta_2}$$は切片の変化、$${\beta_3}$$はトレンドの係数の変化を表しています。
では回帰分析を実行しましょう。
### 回帰分析の実行
# トレンド*構造変化ダミー ⇒ トレンド + 構造変化ダミー + トレンド:構造変化ダミー
result = smf.ols(formula='実質GDP ~ トレンド*構造変化ダミー', data=df2).fit()
display(result.summary())【実行結果】
構造変化によって、切片は$${304.5}$$兆円上方にシフトし、トレンドの傾きは$${7.0}$$減少しています。

予測値を可視化しましょう。
### 実測値と予測値の描画
plt.figure(figsize=(10, 4))
plt.plot(df2['実質GDP'], label='実測値')
plt.plot(result.fittedvalues, color='tab:red', ls='--', label='予測値')
plt.xlabel('年度')
plt.ylabel('実質GDP [兆円]')
plt.title('実質GDPとトレンド変数')
plt.grid(lw=0.5)
plt.legend()
plt.show()【実行結果】
青い実線は実測値、赤い点線は予測値です。
予測値は概ね時系列の傾向を捉えているように見えます。

切片の変化$${+304.5}$$は、バブル期の一時的な実質GDP上昇を捉えている(もしくは吸収している)ように見えます。
傾きの変化$${-7.0}$$は、バブル経済終焉後の低成長を捉えているように見えます。
構造変化があったかどうかを確かめる手法「チャウテスト」は次次回の記事でご紹介いたします!

■ トレンド変数と季節ダミー p.125
実質GDPの四半期の周期性を「季節ダミー」で表現します。
テキストのExcelダウンロードファイルに分析用のデータがないので、以下の内閣府のサイトからデータを取得しました。
【データ引用元】
内閣府 経済社会総合研究所の「統計表(四半期別GDP速報)」
使用データ:
2024年1-3月期 1次速報値-Ⅰ. 国内総生産(支出側)及び各需要項目-実額-四半期-実質原系列(CSV形式)
【お断り】
テキストが使うデータと異なる可能性があり、テキストの分析結果と若干異なる結果になっています。
2012年第三四半期~2019年第三四半期の実質GDPデータを読み込みます。
### データの読み込み
# CSVファイルの読み込み
df3 = pd.read_csv('./data/04_03_gdp.csv', index_col=0)
# 四半期日付のインデックスを設定
df3.index = pd.date_range(start='1994-03-31', periods=df3.shape[0], freq='QE')
df3.index.name = '四半期'
# 2012年第3四半期から2019年第3四半期を抽出
df3 = df3[(df3.index>='2012-09-30') & (df3.index<='2019-9-30')]
# データフレームの表示
print('df3.shape:', df3.shape)
display(df3.head())
display(df3.tail())【実行結果】
実質GDPの単位は 10億円です。

データの前処理を行います。
第二~第四四半期の「3つの四半期ダミー」と「トレンド」を追加します。
1~3月期が第一四半期です。
### 前処理:四半期ダミーとトレンド項の追加
# 四半期ダミーを追加
df3['Q2ダミー'] = (df3.index.quarter == 2).astype(int)
df3['Q3ダミー'] = (df3.index.quarter == 3).astype(int)
df3['Q4ダミー'] = (df3.index.quarter == 4).astype(int)
# トレンド項を追加
df3['トレンド'] = np.arange(1, len(df3)+1)
# 結果の表示
print('df3.shape:', df3.shape)
display(df3.head())【実行結果】
第一四半期は$${Q2ダミー=Q3ダミー=Q4ダミー=0}$$で表現します。

次の式を用いて、回帰分析を実行します。
$$
\begin{align*}
四半期実質GDP =\ &\beta_1 \times Q2ダミー + \beta_2 \times Q3ダミー \\
&+ \beta_3 \times Q4ダミー + \beta_4 \times トレンド + 切片
\end{align*}
$$
四半期ダミー変数の値は$${0}$$か$${1}$$であり、各四半期は次のような数式で表せそうです。
◆ 第一四半期 ◆
切片は第一四半期の切片を示すようです。
トレンドは$${1}$$四半期ごとに$${1}$$増加するので、係数$${\beta_4}$$は四半期ごとの実質GDP増加額(一定額)と読めそうです。
$$
四半期実質GDP = \beta_4 \times トレンド + 切片
$$
◆ 第二四半期 ◆
第二四半期の係数$${\beta_1}$$が切片を調整しているようです。
$$
四半期実質GDP = \beta_4 \times トレンド + (\beta_1 + 切片)
$$
◆ 第三四半期 ◆
$$
四半期実質GDP = \beta_4 \times トレンド + (\beta_2 + 切片)
$$
◆ 第四四半期 ◆
$$
四半期実質GDP = \beta_4 \times トレンド + (\beta_3 + 切片)
$$
では回帰分析を実行しましょう。
切片の大きな桁数を表示する目的で、ols の結果を summary2() で表示します。
### 回帰分析の実行
result = smf.ols(
formula='実質GDP ~ Q2ダミー + Q3ダミー + Q4ダミー + トレンド', data=df3).fit()
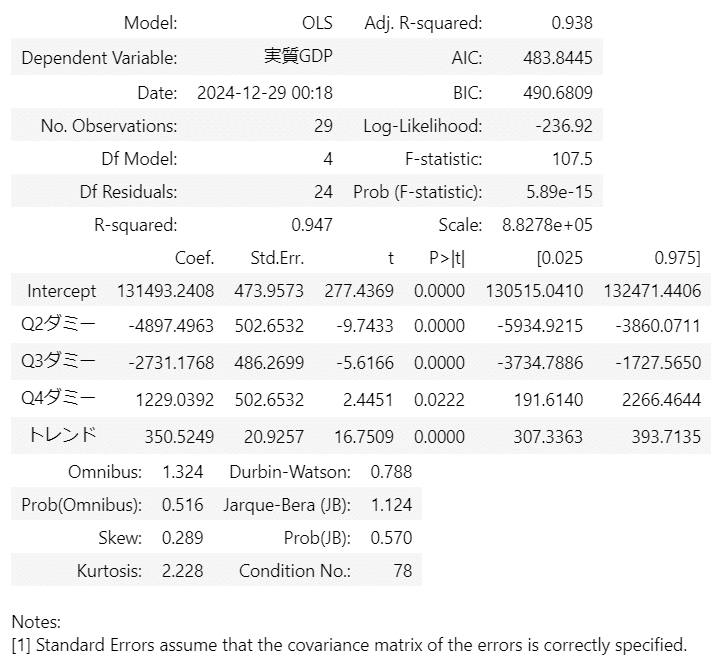
display(result.summary2())【実行結果】
各四半期の切片への影響は、第二四半期と第三四半期がマイナス、第四四半期はプラスです。
予測値を可視化しましょう。
### 実測値と予測値の描画
plt.figure(figsize=(10, 4))
plt.plot(df3['実質GDP'], label='実測値')
plt.plot(result.fittedvalues, color='tab:red', ls='--', label='予測値')
plt.xlabel('四半期')
plt.ylabel('実質GDP [10億円]')
plt.title('トレンド変数と季節ダミーで実質GDPを推定')
plt.ylim(120000, 150000)
plt.grid(lw=0.5)
plt.legend()
plt.show()【実行結果】
青い実線は実測値、赤い点線は予測値です。
予測値は四半期の季節変動を捉えており、トレンドは緩やかに右上がりになっている様子を確認できました。

このグラフより先の期間では、新型コロナウイルスの影響を受けて、予測したトレンドや四半期の周期性とは異なるGDPの動きになっている可能性があります。

4.3 コンジョイント分析
テキストによるとコンジョイント分析は「さまざまな評価指標のうち、回答者が何を重視しているのかが、数値でわかるもの」だそうです。
テキストは、ディズニーランドを題材にして以下のアンケート調査を行っています。
ディズニーランドを楽しむ4つのポイントから組み合わせパターンを作成
11人の学生が各パターンを7段階評価(非常に満足:7点~非常に不満:1点)で評価
回帰分析で推定した係数を用いて各ポイントの満足度を推定

■ 4つのお楽しみポイントと組み合わせパターン p.128
4つのポイントは、「アトラクション」「ショー・パレード」「限定品以外のグッズの購入」「限定品グッズの購入」です。
テキストは「図表 8つの行動パターン」で「4つのポイント」の組み合わせを8パターンを示しています。

アンケート調査では行動パターンごとに7段階評価してもらいます。
例えば、1つ目の行動パターンでは全てのお楽しみポイントを実施するときの評価、2つ目の行動パターンではアトラクションとショー・パレードを実施するときの評価、という感じです。
◆ ◆ ◆
ところで、ポイントの全組み合わせは $${2^4=16}$$で16パターンなのですが、テキストは8パターンに絞り込んで分析を進めるようです。
コンジョイント分析に関するさまざまなWebサイトの情報によると、「直交表」を用いることでパターンの数を減らせるそうです。
ポイント数が4つであり、各ポイントが「含める/含めない」の2水準であることに対応する直交表は$${L_8(2^7)}$$のようです。
次の表が$${L_8(2^7)}$$の直交表です。

行がパターンに対応します。
つまり、アンケート調査を8パターンに絞り込めるということです。
列には4つのポイントを割り当てます。
行と列の交差する点の数値が水準です。
$${1}$$を「パターンに含む」、$${2}$$を「パターンに含まない」としましょう。
$${L_8(2^7)}$$直交表に4つのポイントを割り当てると、テキストの8つの行動パターンが見えてきました!
(注)直交表の行5~8を入れ替えしています。


■ 11人の学生による評価のサマリー p.129
テキストはアンケート調査のサマリーデータを開示しています。
データを読み込みます。
### データの読み込み
# CSVファイルの読み込み
df4 = pd.read_csv('./data/04_04_conjoint.csv')
# 列名の変更
df4 = df4.rename({'ショー・パレード': 'ショーとパレード'}, axis=1)
# インデックスの加工
df4.index = range(1, len(df4)+1)
df4.index.name = 'パターン'
# データフレームの表示
print('df4.shape:', df4.shape)
display(df4)【実行結果】
アンケート評価の平均値を「平均得点」列に設定しています。
各お楽しみポイントはダミー変数になっていて、$${1}$$は「パターンに含む」、$${0}$$は「パターンに含まない」です。

平均得点を満足度と見立てると、全ポイントを実行するパターン1が最も満足度が高そうです(全部楽しみたいですよね!)。
次点は「アトラクション」と「限定品グッズ」です。

■ 閑話休題:パターンと回帰の式
平均得点を目的変数に、お楽しみポイントのダミー変数を説明変数にして、回帰分析を実行します。
回帰の式は以下のような感じ。
$$
\begin{align*}
平均得点 =\ &\beta_1 \times アトラクション + \beta_2 \times ショーとパレード \\
&+ \beta_3 \times 限定以外のグッズ + \beta_4 \times 限定品グッズ \\
&+ 切片
\end{align*}
$$
ダミー変数になっているお楽しみポイントの$${0, 1}$$を回帰の式に当てはめてみましょう。
$$
\begin{array}{c:ccccc}
パターン & 平均点 & アトラ & ショー & グッズ & 限定 & 切片\\
\hline
1 & 6.63 = & +\beta_1 & +\beta_2 & +\beta_3 & +\beta_4 & + \beta_0\\
2 & 5.54 = & +\beta_1 & +\beta_2 & & & +\beta_0 \\
3 & 5.27 = & +\beta_1 & & +\beta_3 & & + \beta_0\\
4 & 5.90 = & +\beta_1 & & & +\beta_4 & + \beta_0\\
5 & 2.09 = & & & & & + \beta_0\\
6 & 3.36 = & & & +\beta_3 & +\beta_4 & + \beta_0\\
7 & 4.09 = & & +\beta_2 & & +\beta_4 & + \beta_0\\
8 & 3.72 = & & +\beta_2 & +\beta_3 & & + \beta_0\\
\end{array} \\
$$
8つのパターンの中に、ダミー変数の係数が4つずつ含まれています。
ダミー変数の係数は「切片」の調整のような働きをするようです。
(ダミー変数の係数は傾きでは無さそうです)
また任意の2列について、係数あり/なしの組み合わせが2組ずつ存在しています。
後者が直交表の特徴だそうです。

■ 回帰分析で推定した係数を用いて各ポイントの満足度を推定 p.129
いよいよ分析開始です!
回帰分析を実行します。
### 回帰分析の実行
formula = '''
平均得点 ~ アトラクション + ショーとパレード + 限定以外のグッズ + 限定グッズ
'''
result = smf.ols(formula=formula, data=df4).fit()
display(result.summary())【実行結果】
自由度調整済み決定係数(Adj. R-squared)は$${0.962}$$。
当てはまりがかなり良い感じ。

では「ポイントごと」の満足度を探りましょう。
係数は「部分効用」と呼ばれます。
部分効用が高いのは「アトラクション」($${2.5}$$)、「ショーとパレード」($${0.8}$$)、「限定グッズ」($${0.8}$$)です。
「限定以外のグッズ」はテキストによると「$${t$}$値が$${1.64}$$と低く」目的変数「への影響が小さいことがわかります」とのこと。
部分効用の2倍は「重要度」、重要度の比率は「相対重要度」と呼ばれます。
テキストによると「重要度が高い特性」(ここではお楽しみポイント)「ほど、満足度の高い特性といえる」とのこと。
相対重要度を可視化しましょう。
### 相対的重要度の可視化
## 重要度の算出
# 重要度の算出 係数の2倍
importances = abs(result.params[1:]) * 2
# 相対的重要度(重要度全体に占める比率)の算出
importances_prop = importances / importances.sum()
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 相対的重要度の横グラフの描画 ※pandasで描画
importances_prop.sort_values().plot.barh(
xlim=(0, 0.65), alpha=0.7,
title='遊園地のお楽しみポイントの相対的重要度\nコンジョイント分析',
ax=ax)
# 相対的重要度の値を表示
for i, v in enumerate(importances_prop.sort_values()):
ax.annotate(text=f'{v:.1%}', xy=(v+0.01, i), fontsize=12)
# x軸目盛りを%表示 ※ from matplotlib.ticker import PercentFormatter
ax.xaxis.set_major_formatter(PercentFormatter(xmax=1))
# 修飾
ax.grid(lw=0.5, axis='x')
plt.show()【実行結果】
アトラクションの満足度が圧倒的に高いです!

お楽しみポイントの「組み合わせの一部の評価」から、お楽しみポイント「個別の満足度を推定」できるって、なんだか不思議です。
今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
