
「Pythonによる異常検知」を寄り道写経 ~ 第2章2.4節「高度な特徴抽出による異常検知」⑤制約付きボルツマンマシン(RBM)
第2章「非時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第2章「非時系列データにおける異常検知」2.4節「高度な特徴抽出による異常検知」の通称「寄り道写経」を取り扱います。
5回連続で高度な特徴抽出技術を利用した異常検知を寄り道写経します!
今回は 制約付きボルツマンマシン(RBM)による異常検知です。
ではテキストを開いて異常検知の旅に出発です🚀

はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.4 高度な特徴抽出による異常検知
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
制約付きボルツマンマシン(以下、RBMと略します)で異常検知を行います。
学習データで異常検知モデルを作成して、未知データの異常検知を行います。
学習データと未知データは前回と同じ3次元データです。

RBMの実装は難しく、一人でやり遂げることができませんでした。。。
以下のWebサイトよりtaka256様のRBMのコードを引用いたしました。
ありがとうございます!
RBMを動かすことができて嬉しかったです。
この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
制約付きボルツマンマシン(RBM)
制約付きボルツマンマシン(Restricted Bolzmann Machines: RBM)を異常検知に用いるアイデアは主成分分析やオートエンコーダとよく似て、「次元削減」と「再高次元化」です。
RBMの概要はぜひテキスト(図1.40あたり)をご覧ください。
また、次のWebサイトではとてもやさしくRBMを説明しています。
誤差関数と異常検知のマリアージュ💞
異常度は入力データと出力データのユークリッド距離(L2ノルム)です。

準備
1.学習データの作成と可視化
前回と同じ3次元データを作成します。
最初の2次元は前回までと同じ300個の乱数データを作成します。
200個はグループ0、100個はグループ1を想定して、別々の2変量正規分布で乱数を作成します。
3次元目は連続一様分布乱数で作成します。
### データの作成 ※3変数
# 乱数生成器の設定
rng = np.random.default_rng(seed=1)
# 乱数生成器の設定
rng = np.random.default_rng(seed=1) # 23 or 24
# グループ0の200個のデータ作成:2変量正規分布乱数
group0 = rng.multivariate_normal(mean=[1, 1], cov=[[0.3, 0.081], [0.081, 0.3]],
size=200)
# グループ1の100個のデータ作成:2変量正規分布乱数
group1 = rng.multivariate_normal(mean=[-1, -1], cov=[[0.1, 0.009], [0.009, 0.1]],
size=100)
# 3次元目を追加(一様分布乱数)
data_3rd = rng.uniform(low=-1, high=1, size=300).reshape(-1, 1)
# データの統合
data = np.vstack([group0, group1])
data = np.hstack([data, data_3rd])
print('data.shape:', data.shape)
print(data[:5, :], '…')
# グループラベルの作成
label_true = np.hstack([np.zeros(200), np.ones(100)]).astype(int)
print('\nグループラベル:', label_true[:10], '…')【実行結果】

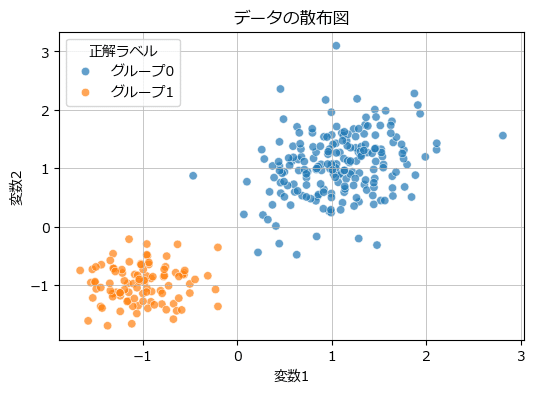
学習データの散布図を描画して、分布などを確認しましょう。
### データの散布図の描画 ※変数1,2の組み合わせ(以後同様)
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=label_true, alpha=0.7,
palette=['tab:blue', 'tab:orange'], ax=ax)
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['グループ0', 'グループ1'], title='正解ラベル')
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='データの散布図')
ax.grid(lw=0.5);【実行結果】
実のところ、RBMでクラスタリングを行わないので、グループ別の表記はあまり意味が無いかもです。

異常検知モデルの構築
テキストの STEP に沿って、学習データによる異常検知モデルの構築に取り組みます。
1.STEP 1:RBMの学習
ゆっくり順を追って進めてまいります。
■ RBMの定義
taka256様のコードを引用いたします。
なお★印の箇所は引用コードを改変しました。
特に sigmoid 関数のオーバーフロー対策には、chersky様のWebサイトのコードを引用いたしました。
ありがとうございます!
### 制約付きボルツマンマシン関数の定義 ★印を改造
# 引用元 https://developers.agirobots.com/jp/deep-learning-2020-rbm/
class RBM():
def __init__(self, v_num, h_num, seed=11): # ★mod seed追加
"""
=引数=
v_num:可視ニューロンの数
h_num:隠れニューロンの数
=重みパラメータと状態パラメータの定義=
self.w:可視ニューロンと隠れニューロン間の重み結合を表す行列
self.v_b:可視ニューロンの持つバイアス
self.h_b:隠れニューロンが持つバイアス
self.v:可視ニューロンの状態を表すベクトル
self.h:隠れニューロンの状態を表すベクトル
"""
self.v_num = v_num
self.h_num = h_num
self.seed = seed # ★add 乱数シード
self.w = np.zeros((v_num, h_num), dtype=np.float32)
self.v_b = np.zeros((v_num, ), dtype=np.float32)#.reshape(-1, v_num)
self.h_b = np.zeros((h_num, ), dtype=np.float32)#.reshape(-1, h_num)
## ★mod sigmoid関数のオーバーフロー対策
# 引用元 https://qiita.com/chersky/items/d74c9662a25c4e84565f
# def sigmoid(self, x):
# return 1 / (1 + np.exp(-x))
def sigmoid(self, x):
return np.exp(np.minimum(x, 0)) / (1 + np.exp(- np.abs(x)))
def sampling(self, p):
# _s = p - np.random.random_sample(p.shape)
_s = p - self.rng.random(p.shape) # ★mod 乱数生成器使用
# return np.where(0, 1, _s > 0)
return np.where(_s > 0, 1, 0) # ★mod 理解しやすい形式
def v_to_h(self, x):
"""
可視ニューロンのバイナリ値から隠れニューロンの値を導出
シグモイド関数を使い確率へ写像
入力データの型は[batch_size, feature_num]を想定
"""
return self.sigmoid(x @ self.w + self.h_b)
def h_to_v(self, x):
"""
隠れニューロンのバイナリ値から可視ニューロンの値を導出
シグモイド関数を使い確率へ写像
入力データの型は[batch_size, feature_num]を想定
"""
return self.sigmoid(x @ self.w.T + self.v_b)
def fit(self, x, eta, epochs):
err = []
self.rng = np.random.default_rng(self.seed) # ★add 乱数生成器の初期化
for epoch in range(epochs):
v0 = x
p_h0 = self.v_to_h(v0)
h0 = self.sampling(p_h0)
v1 = self.sampling(self.h_to_v(h0))
p_h1 = self.v_to_h(v1)
self.w = self.w + eta*(v0.T @ p_h0 - v1.T @ p_h1)
self.v_b = self.v_b + eta*(np.mean(v0, axis=0) - np.mean(v1, axis=0))
self.h_b = (self.h_b + eta*(np.mean(p_h0, axis=0)
- np.mean(p_h1, axis=0)))
err.append(np.mean(np.abs(v0-v1)))
return err
def predict(self, x): # ★mod:関数名の変更
v0 = x
self.rng = np.random.default_rng(self.seed) # ★add 乱数生成器の初期化
h0 = self.sampling(self.v_to_h(v0))
v1 = self.sampling(self.h_to_v(h0))
return v1【実行結果】なし
■ RBMの学習
RBMを動かします!
隠れ層の数を 6 にしました。
入力データの次元数 3 よりも大きい値です。
エポック数は 500 です。
### RBMの学習
## 初期値設定
num_visible = data.shape[1] # 可視層の数=説明変数数=データの列数
num_hidden = 6 # 隠れ層の数
seed = 15 # 乱数シード # 11, 15, 16, 17, 18, 25
## 学習の実行
# RBMインスタンス生成
rbm = RBM(v_num=num_visible, h_num=num_hidden, seed=seed)
# RBMの学習
rbm_error = rbm.fit(data, eta=0.1, epochs=500)【実行結果】なし
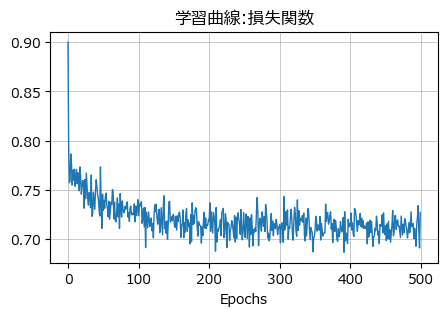
学習曲線(損失曲線)を可視化します。
### 損失関数の可視化
plt.figure(figsize=(5, 3))
plt.plot(rbm_error, lw=1)
plt.xlabel('Epochs')
plt.title('学習曲線:損失関数')
plt.grid(lw=0.5);【実行結果】
まずまず収束しているのではないでしょうか。

2.STEP 2:異常度の算出
RBMで学習データの予測値を算出して、予測値と入力データのユークリッド距離を異常値とします。
### STEP2 異常度の算出
### 異常度関数(テキスト120頁の式34)α(X)=‖NN(W, X)-X‖²
# RBMの予測値の算出
rbm_pred = rbm.predict(data)
# 異常度αの算出 : nn_predとデータの差(つまり誤差)のユークリッド距離
anomaly_score = np.linalg.norm(rbm_pred - data, ord=2, axis=1)
# 異常度の表示
print('anomaly_score.shape:', anomaly_score.shape)
print('anomaly_score[:5] :', anomaly_score[:5], '…')【実行結果】
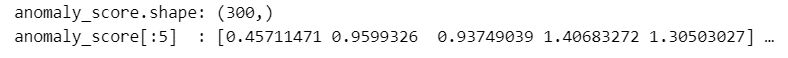

3.STEP 3:異常度の閾値の算出
分位点法による閾値を算出します。
分位点は 1% です。
### STEP3 異常度の閾値の算出 by 分位点法
# 分位%点の設定
q = 0.01
# 閾値の算出
num_quantile = int(round(len(anomaly_score) * q, 0))
anomaly_thres = sorted(anomaly_score)[::-1][num_quantile - 1]
# 閾値の表示
print('分位点数:', num_quantile)
print('閾値:', anomaly_thres)【実行結果】
閾値はおよそ 2.56 です。
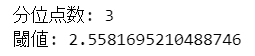
4.STEP 3-2:学習データで異常検知を確認
学習データの異常度に閾値を適用して異常検知を実行し、結果を可視化します。
### STEP3-2 学習データの異常検知
# 正常/異常ラベルの算出
anomaly_label = np.array((anomaly_score >= anomaly_thres) + 0)
# 算出結果の表示
print('anomaly_label.shape:', anomaly_label.shape)
print('anomaly_label[:10] :', anomaly_label[:10], '…')
print('異常データ数:', anomaly_label.sum())【実行結果】
学習データのうち、3点が異常判定となるモデルになりました。

異常検知の結果を可視化します。
### STEP3-3 異常度と閾値を可視化して確認
## 異常度と閾値の可視化関数の定義
def plot_anomaly1(a_score, a_threshold, a_label, q):
# 設定
palette = ['tab:blue', 'tab:red']
sizes = [40, 80]
labels = ['正常', '異常']
# 正常データがない場合
if sum(a_label == 0) == 0:
palette = ['tab:red']
sizes = [80]
labels = ['異常']
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# データの散布図の描画
sns.scatterplot(x=range(len(a_score)), y=a_score,
hue=a_label, palette=palette,
size=a_label, sizes=sizes)
# 閾値の水平線の描画
ax.axhline(a_threshold, color='tab:red', ls='--')
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=labels, bbox_to_anchor=(1, 1))
ax.set(xlabel='データ番号', ylabel='異常度 $\\alpha$',
title=f'AutoEncoderによる異常度\n閾値 {a_threshold:.3f} (q={q:.0%})')
ax.grid(lw=0.5)
plt.show()
## 異常度の可視化
plot_anomaly1(anomaly_score, anomaly_thres, anomaly_label, q)【実行結果】
異常度の大きな順から3番目の異常データ点付近が閾値な感じがいたします。
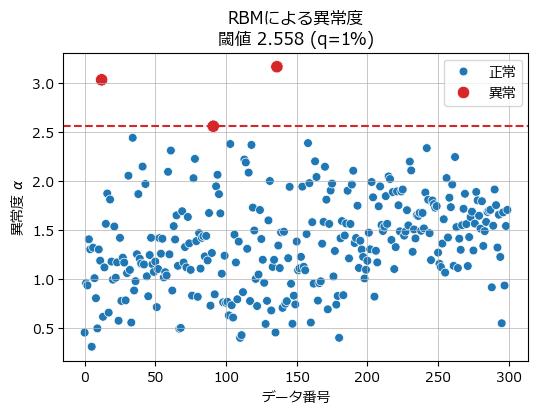
前回までのコレクションを飾ります。
三者三様の異常値をご堪能ください!
(参考:オートエンコーダ)
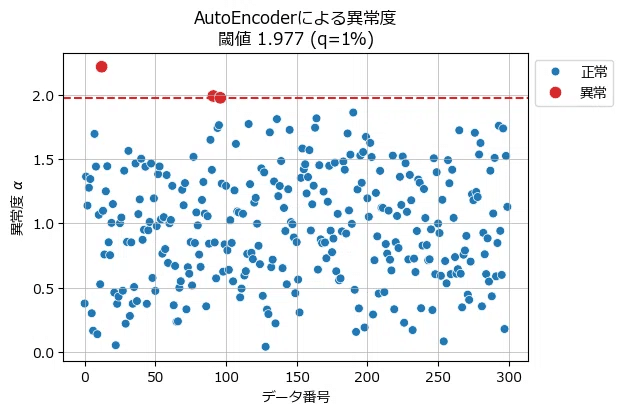
(参考:主成分分析)
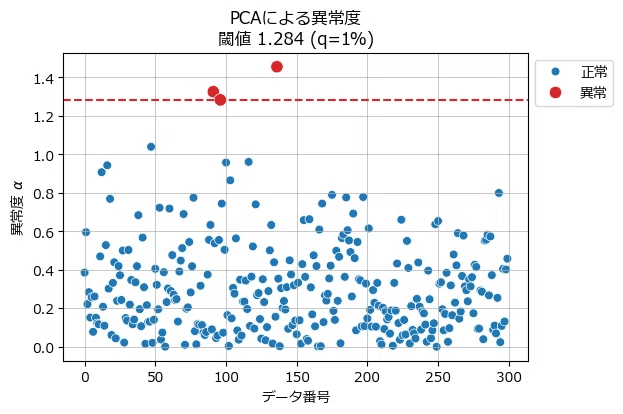
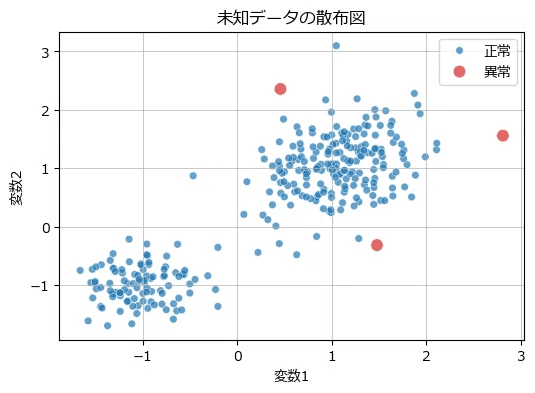
変数1、変数2の散布図の形式で異常データを見てみましょう。
### 異常データの散布図の描画
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=anomaly_label,
palette=['tab:blue', 'tab:red'], ec='white', alpha=0.7,
size=anomaly_label, sizes=[30, 80], ax=ax)
handles, _ = ax.get_legend_handles_labels()
ax.legend(handles=handles, labels=['正常', '異常'])
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの散布図')
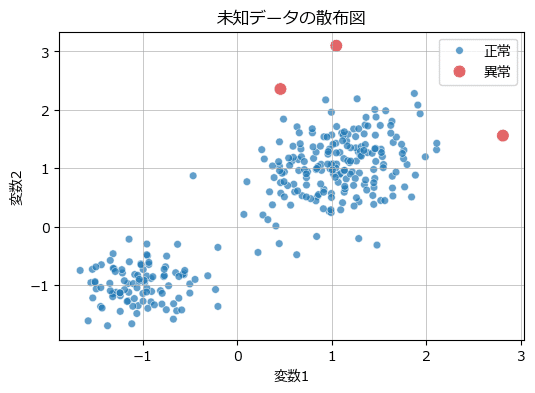
ax.grid(lw=0.5);【実行結果】
赤いデータ点を異常と捉えたようです。
データの塊から外れている点をうまく異常と捉えているようです。
前回までのコレクションを飾ります。
三者三様の異常値をご堪能ください!
(参考:オートエンコーダ)
(参考:主成分分析)

未知データの準備
未知データを作成して、さきほど構築した異常検知モデルに適用して異常検知しましょう!
1.未知データの作成
### 未知データの作成
data_new = np.array([[-1, 2, -0.5], [-1, 0.3, 0.8], [0, -1.5, 0.2],
[0, -1, -0.4], [1, -1, 1], [2, 0, -1]])
print('未知データ:')
print(data_new)【実行結果】
6個のデータを作成しました。
前回の未知データと同じです。

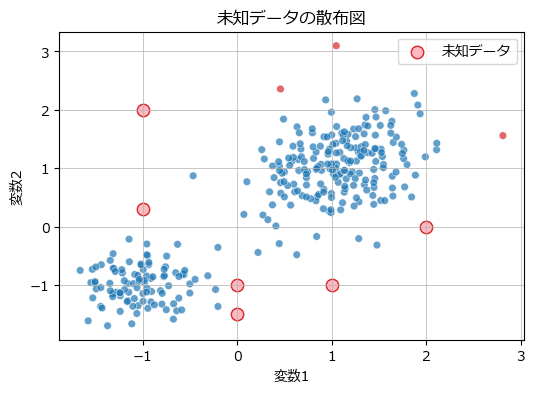
未知データを可視化します。
### 未知データの可視化
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=anomaly_label,
palette=['tab:blue', 'tab:red'], ec='white', alpha=0.7,
size=anomaly_label, sizes=[30, 30], legend=False, ax=ax)
# 未知データの散布図の描画
ax.scatter(data_new[:, 0], data_new[:, 1], color='lightpink', ec='tab:red',
s=80, label='未知データ')
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの散布図')
ax.legend()
ax.grid(lw=0.5);【実行結果】

未知データの異常検知
いよいよ本番です!
テキストの STEP に沿って、未知データの異常検知に取り組みます。
1.STEP 4:未知データの異常度の算出
学習済みのRBM器 rbm を用いて、未知データの超高次元化・再低次元化を実行し、異常度を計算します。
### STEP4 未知データの異常度の算出
# RBMの予測値の算出
rbm_new_pred = rbm.predict(data_new)
# 異常度αの算出 : nn_predとデータの差(つまり誤差)のユークリッド距離
anomaly_score_new = np.linalg.norm(rbm_new_pred - data_new, ord=2, axis=1)
print('未知データの異常度 :', anomaly_score_new)【実行結果】
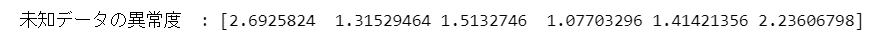
2.STEP 5 未知データの異常検知
異常度計算・閾値を適用して異常データを炙り出します!
### STEP5 未知データの異常検知
anomaly_label_new = np.array((anomaly_score_new >= anomaly_thres) + 0)
print('未知データの異常検知:', anomaly_label_new)【実行結果】
未知データの1番目が異常判定されました!
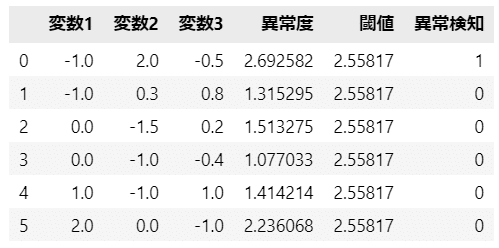
未知データの異常検知結果をデータフレーム化しましょう。
### 未知データの異常検知結果のデータフレームの作成
data_new_df = pd.DataFrame(data_new, columns=['変数1', '変数2', '変数3'])
data_new_df['異常度'] = anomaly_score_new
data_new_df['閾値'] = anomaly_thres
data_new_df['異常検知'] = anomaly_label_new
display(data_new_df)【実行結果】

3.異常検知結果を可視化
未知データの異常検知結果をさまざまな可視化手法で堪能しましょう。
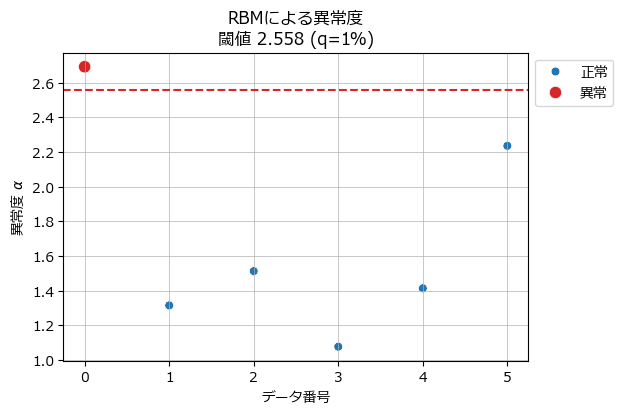
① 異常度の散布図
### 異常度の可視化
plot_anomaly1(anomaly_score_new, anomaly_thres, anomaly_label_new, q)【実行結果】
未知データの異常度はさまざまな値をとっていることが分かります。
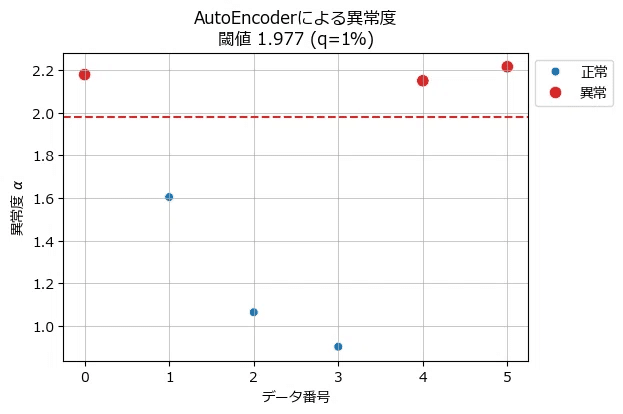
前回までのコレクションを飾ります。
三者三様の異常値をご堪能ください!
(参考:オートエンコーダ)
(参考:主成分分析)
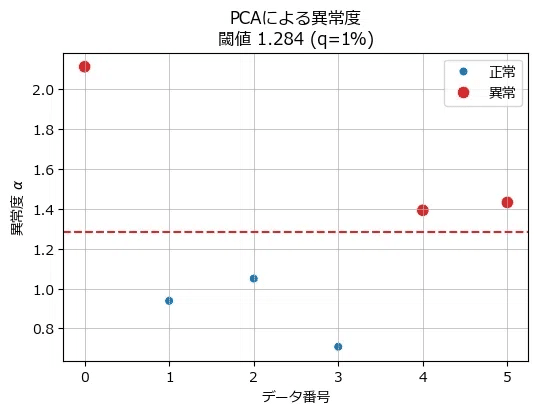
② 2変数の散布図に正常・異常をマップ
学習データを含む2変数の散布図に未知データを追加してみましょう。
未知データは正常・異常を識別してプロットします。
### 未知データの異常検知の可視化
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 学習データの散布図の描画
sns.scatterplot(x=data[:, 0], y=data[:, 1], hue=anomaly_label,
palette=['tab:blue', 'tab:red'], ec='white', alpha=0.7,
size=anomaly_label, sizes=[30, 30], legend=False, ax=ax)
# 未知データの散布図の描画
sns.scatterplot(x=data_new[:, 0], y=data_new[:, 1],
hue=anomaly_label_new, palette=['tab:blue', 'tab:red'],
alpha=0.7, ec='wheat',
style=anomaly_label_new, markers=['o', 'X'],
size=anomaly_label_new, sizes=[200, 250], legend=False,
ax=ax)
for i in range(len(data_new)):
ax.annotate(text=i, xy=data_new[i, :2]+0.12, fontsize=14)
# 凡例
ax.scatter([], [], marker='o', c='tab:blue', ec='wheat', s=70, label='正常')
ax.scatter([], [], marker='X', c='tab:red', ec='wheat', s=100, label='異常')
ax.legend(bbox_to_anchor=(1.2, 1))
# 修飾
ax.set(xlabel='変数1', ylabel='変数2', title='未知データの異常検知')
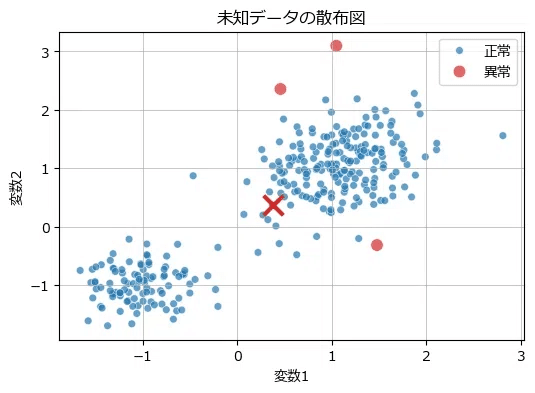
ax.grid(lw=0.5);【実行結果】
大きく外れている点が異常になっています。
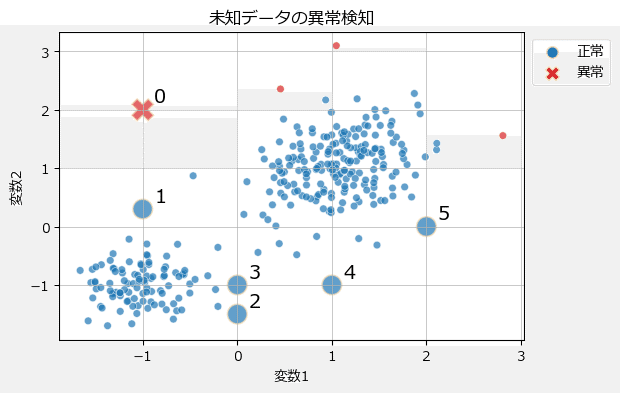
前回までのコレクションを飾ります。
三者三様の異常値をご堪能ください!
(参考:オートエンコーダ)
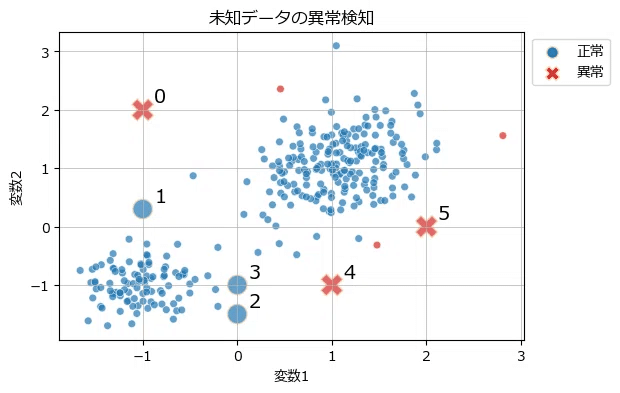
(参考:主成分分析)
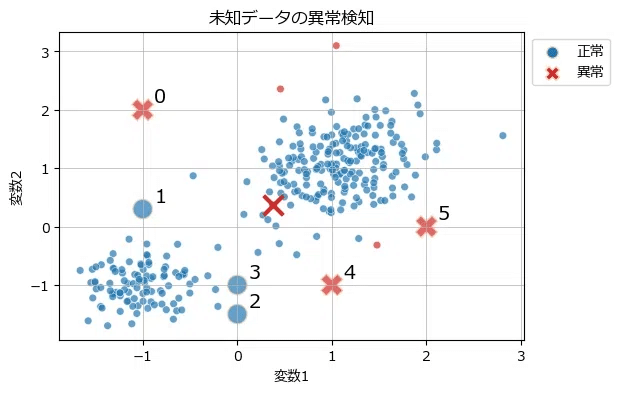
今回の寄り道写経は以上です。
高度な特徴抽出技術を利用した異常検知も今回で完了です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
