
「Pythonによる異常検知」を寄り道写経 ~ 第2章2.3節「非正規分布に基づく異常検知」局所外れ値因子法(LOF法)
第2章「非時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第2章「非時系列データにおける異常検知」2.2節「非正規分布に基づく異常検知」の通称「寄り道写経」を取り扱います。
今回はデータが正規分布に従うと仮定しない場合の局所外れ値因子(LOF)法による異常検知を寄り道写経します!
ではテキストを開いて異常検知の旅に出発です🚀

はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
2.3 非正規分布に基づく異常検知
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
学習データのみ使用する異常検知となります。
局所外れ値因子(LOF)法をscikit-learnのライブラリで実践
この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
# 機械学習
from sklearn.neighbors import LocalOutlierFactor
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
局所外れ値因子(LOF)法
局所外れ値因子(LOF)法(LOF: Local Outlier Factor)は次のような特徴があり、正規分布に従っていないデータの異常値を扱えるそうです。
密度のばらつきがあるデータのk近傍法
データ間の距離を特徴として抽出し、異常度を定義

1.データの読み込みと可視化
テキストのデータをお借りします。
### データの読み込み ★テキストのデータを引用
data = pd.read_csv('./data/Davis_1_2.csv').values[:, 2:4]
print('data.shape:', data.shape)
print(data[:10, :], '…')【実行結果】
1列目は体重(kg)、2列目は身長(cm)です。

散布図を描画します。
### データの可視化
sns.scatterplot(x=data[:, 0], y=data[:, 1])
plt.xlabel('体重 [kg]')
plt.ylabel('身長 [cm]')
plt.grid(lw=0.5);【実行結果】
左下の群と中央上の群に分かれている感じです。

2.異常検知の実行
scikit-leanr の LocalOutlierFactor を使用してLOF法を実行します。
正常・異常を識別するLOFラベルを実行結果として取得できます。
引数 k で近傍点の数$${k}$$を設定します。
引数 contamination で異常データの割合的な数値を設定します。
(ピッタリ異常割合にはなりません)
### scikit-learnのLocalOutlierFactorの実行 ★テキストと異なる実装
## LOFの設定値
# kの設定
k = 10
# contamination(異常割合的な値)の設定
contamination = 0.1
## LOFの実行
# LOF分類器の設定
clf_lof = LocalOutlierFactor(n_neighbors=k, contamination=contamination)
# LOFの実行、正常/異常ラベルの取得 外れ値:-1, 通常値:1
lof_labels = clf_lof.fit_predict(data)
# ラベル値の変更 外れ値:1, 通常値:0
lof_labels = np.where(lof_labels == -1, 1, 0)
print('正常/異常LOFラベル:', lof_labels[:10], '…')【実行結果】
1STEPで正常・異常の判別ができました!

3.異常度と閾値の確認
LOF法が正常・異常の判別に用いたスコア(LOF)と閾値を表示します。
LOF法を実行して得た clf_lof に対して「negative_outlier_factor_」でスコアを取得でき、「offset_」で閾値を取得できます。
両数値は負値なので、$${-1}$$を掛けて正値に変換しています。
### LOFスコアと閾値の取得(元値が負のため-1を掛けて正値に変換)
score = -1 * clf_lof.negative_outlier_factor_
thres = -1 * clf_lof.offset_
print('LOFスコア:', score[:5], '…')
print('閾値 :', thres)【実行結果】

4.異常検知の可視化
3つのグラフを描画します。
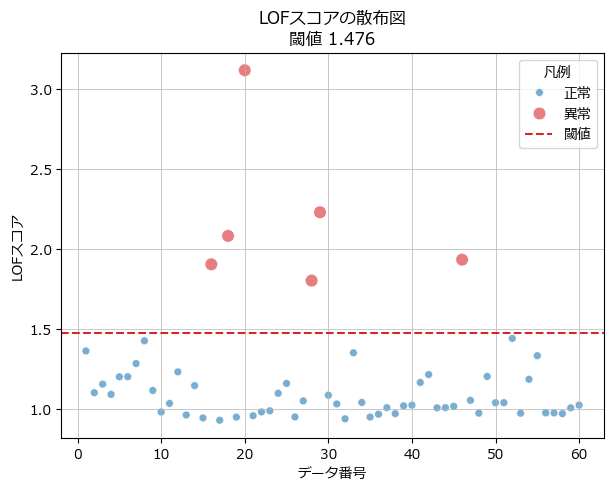
1つ目は異常度と閾値の散布図です。
### LOFスコアによる異常検知表現
# 描画領域の設定
fig, ax = plt.subplots(figsize=(7, 5))
# 異常度の散布図の描画
sns.scatterplot(x=range(1, len(score)+1), y=score, alpha=0.6,
hue=lof_labels, palette=['tab:blue', 'tab:red'],
size=lof_labels, sizes=[30, 80], ax=ax)
# 閾値の水平線の描画
ax.axhline(thres, color='tab:red', ls='--', label='閾値')
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(title='凡例', handles=handles, labels=['正常', '異常', '閾値'])
# 修飾
ax.set(xlabel=r'データ番号', ylabel=r'LOFスコア',
title=f'LOFスコアの散布図\n'
f'閾値 {thres:.3f}')
ax.grid(lw=0.5);【実行結果】
学習データのうち6点が異常です。
なかなかいい感じに異常判別しているような気がします。
続いて、テキストの図2.12に相当する2つの図を描画します。
1つ目は体重・身長の散布図で異常点を表現します。
### テキスト図2.12左の再現
# 描画領域の指定
fig, ax = plt.subplots(figsize=(7, 4))
# LOFで得たラベルを加味してxyの散布図を描画
sns.scatterplot(ax=ax, x=data[:, 0], y=data[:, 1], alpha=0.7,
hue=lof_labels, palette=['tab:blue', 'tab:red'],
size=lof_labels, sizes=[40, 70])
# 凡例
handles, _ = ax.get_legend_handles_labels()
ax.legend(loc='upper left', handles=handles, labels=['正常', '異常'])
# 修飾
ax.set(xlabel='体重[kg]', ylabel='身長[cm]',
title='LOFラベルで異常点を識別した散布図')
plt.grid(lw=0.5);【実行結果】
異常値、そう来たか!という所感です。
右下の群は密度が高いからか、それほど離れていないように感じる点が1点異常となっています。
中央上の群は密度がそれほど高くなくからか、異常点もいい感じに群から離れている感じがします。

次の図は $${k}$$に$${10,15,20}$$を設定してLOF法を実行した結果の描画です。
### テキスト図2.12右の再現
## 初期設定
# kの値
ks = [10, 15, 20]
# マーカーの色の設定
colors = ['tab:blue', 'tab:red', 'tab:green']
# マーカーの形状の設定
markers = ['o', 'o', 's']
## 描画処理
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 5))
# 3つのkごとにLOF実行と描画を繰り返し処理
for i, (k, c, m) in enumerate(zip(ks, colors, markers)):
# LOFの実行
clf_lof = LocalOutlierFactor(n_neighbors=k, contamination=contamination)
pred_lof = clf_lof.fit_predict(data)
# 異常度の取得
anomaly_score = clf_lof.negative_outlier_factor_ * -1
# 散布図の描画
ax.scatter(range(1, data.shape[0]+1), anomaly_score,
color=c, alpha=0.5, s=30, marker=m, label=f'k={k}')
# k=20のときの閾値の水平線の描画
ax.axhline(clf_lof.offset_ * -1, color='tab:red', ls='--',
label='k=20の閾値')
# 修飾
ax.set(ylim=(0.5, 3.5), xlabel='データ番号', ylabel='LOF')
ax.grid(lw=0.5)
ax.legend()
plt.show()【実行結果】
テキストではデータ点ごとに局所異常度(LOF)の値を比較して、LOF法の収束を確認しています。

今回の寄り道写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
