
「Pythonによる異常検知」を寄り道写経 ~ 第3章3.4節「機械学習による時系列データの解析」②再帰型ニューラルネットワーク
第3章「時系列データにおける異常検知」
書籍の著者 曽我部東馬 先生、監修 曽我部完 先生
この記事は、テキスト「Pythonによる異常検知」第3章「時系列データにおける異常検知」3.4節「機械学習による時系列データの解析」の通称「寄り道写経」を取り扱います。
前回から2回連続で機械学習を利用した時系列データ解析を寄り道写経します!
今回は 再帰型ニューラルネットワーク(LSTM)です。
※異常検知はありません。
ではテキストを開いて時系列データ解析の旅に出発です🚀

はじめに
テキスト「Pythonによる異常検知」のご紹介
このシリーズは書籍「Pythonによる異常検知」(オーム社、「テキスト」と呼びます)の寄り道写経です。
テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる1冊です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第1版第6刷、著者 曽我部東馬、監修者 曽我部完、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
3.4 機械学習による時系列データの解析
主に Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
今回の寄り道ポイントです。
再帰型ニューラルネットワークの一種、 LSTM(Long Short Term Memory)のシンプルなモデルを PyTorch で実装して、多変数の時系列データ解析を行います。
この記事で用いるライブラリをインポートします。
### インポート
# 数値計算、確率計算
import numpy as np
import pandas as pd
# 時系列解析
import statsmodels.api as sm
# PyTorch
import torch
import torch.nn as nn
from torch.utils.data import TensorDataset, DataLoader
# 機械学習
from sklearn.preprocessing import LabelEncoder, MinMaxScaler
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# 設定
seed = 1234 # 乱数シード
LSTM
LSTMは時間の系列を考慮できる再帰型ニューラルネットワークのモデルです。
今回は入力層 8、LSTM層 200、出力層 1 のモデルです。

データの確認
1.データの読み込み
テキストのデータを引用いたします。
北京の米国大使館で観測した天候・大気(目的変数はPM2.5濃度)のデータセットです。
### データの読み込み ※テキストのコードを引用、一部改変
# データの読み込み
data_orgn = pd.read_csv('./data/pollution_5variable.csv', header=0, index_col=0)
print('data_orgn.shape', data_orgn.shape)
display(data_orgn.head())
# Numpy配列化
values = data_orgn.values
# 目的変数の取り出し
dataset = data_orgn['pollution']【実行結果】
1時間毎の8変数の時系列データです。

2.ADF検定
データの定常性を確認するため、目的変数「pollution」のADF検定を実行します。
帰無仮説は「データは非定常である」です。
statsmodels の adfuller を利用します。
### 目的変数のADF検定 ※テキストと異なるコード
# ADF検定の実行
adf_result = sm.tsa.stattools.adfuller(dataset)
# ADF検定結果の表示
print(f'ADF統計量: {adf_result[0]:.6f} p値: {adf_result[1]:.6f}')
print(f'棄却限界値:', end='')
for k, v in adf_result[4].items():
print(f' {k}: {v:.3f}', end='')【実行結果】
有意水準を 5% とすると p値が 0.05 未満なので帰無仮説は棄却され、データは定常である、と解釈できます。

3.自己相関の確認
statsmodels の plot_acf(コレログラム)と plot_pacf(偏自己相関プロット)を利用します。
テキストの図3.30に相当します。
### 目的変数のコレログラムと偏自己相関プロットの描画 ※テキストと異なるコード
# 自己相関・偏自己相関分析の描画関数の定義
def plot_acf_pacf(data, lags=20):
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# 自己相関分析(コレログラム)の描画
sm.graphics.tsa.plot_acf(data, lags=lags, markersize=3, ax=ax1,
title='自己相関分析', auto_ylims=True)
ax1.set(xlabel='ラグ $h$', ylabel='自己相関')
# 偏自己相関分析の描画
sm.graphics.tsa.plot_pacf(data, lags=lags, markersize=3, ax=ax2,
title='偏自己相関分析', auto_ylims=True)
ax2.set(xlabel='ラグ $h$', ylabel='偏自己相関')
# 修飾
plt.tight_layout();
# 描画
plot_acf_pacf(dataset, lags=80)【実行結果】
偏自己相関より、ラグ1の自己相関があります。


データセットの作成
テキストのコードを引用して、学習データとテストデータを揃えます。
1.データ変換関数
テキストオリジナルコードを引用します。
### テキストのデータ変換関数 ※テキストのコードを引用
# convert series to supervised learning
def series_to_supervised(data, n_in=2, n_out=1, dropnan=True):
n_vars = 1 if type(data) is list else data.shape[1]
df = pd.DataFrame(data)
cols, names = list(), list()
# input sequence (t-n, ... t-1)
for i in range(n_in, 0, -1):
cols.append(df.shift(i))
names += [('var%d(t-%d)' % (j+1, i)) for j in range(n_vars)]
# forecast sequence (t, t+1, ... t+n)
for i in range(0, n_out):
cols.append(df.shift(-i))
if i == 0:
names += [('var%d(t)' % (j+1)) for j in range(n_vars)]
else:
names += [('var%d(t+%d)' % (j+1, i)) for j in range(n_vars)]
# put it all together
agg = pd.concat(cols, axis=1)
agg.columns = names
# drop rows with NaN values
if dropnan:
agg.dropna(inplace=True)
return agg【実行結果】なし
2.データの前処理
テキストオリジナルコードを引用いたします。
### データの前処理 ※テキストのコードを引用
# 風向きwnd_dirを整数値に変換
encoder = LabelEncoder()
values[:, 4] = encoder.fit_transform(values[:, 4])
# 全項目のデータ型をfloat32に変換
values = values.astype('float32')
# 全項目のデータ正規化(MinMax法)
scaler = MinMaxScaler(feature_range=(0, 1))
scaled = scaler.fit_transform(values)
# 変数のラグ特徴量の作成:ラグ1
reframed = series_to_supervised(scaled, n_in=1, n_out=1)
reframed.drop(reframed.columns[list(range(9, 16))], axis=1, inplace=True)
# 加工後のデータを表示
print('reframed.shape:', reframed.shape)
display(reframed.head())【実行結果】

3.学習データとテストデータの分割
テキストオリジナルコードを引用いたします。
### 学習データとテストデータの分割 ※テキストのコード引用
# 前準備
values = reframed.values # データフレームからNumpy配列へ変換
n_train_hours = 10 * 24 # 学習データは最初の10日間
# 学習データとテストデータに分割
train = values[:n_train_hours, :]
test = values[n_train_hours:, :]
# 説明変数var1(t-1)~var8(t-1)と目的変数var1(t)に分割
train_X, train_y = train[:, :-1], train[:, -1]
test_X, test_y = test[:, :-1], test[:, -1]【実行結果】なし

モデルの構築
pytorchでLTSMモデルを構築します。
1.データセットの作成
pytorchのデータローダを作成します。
### データセットの作成
# 設定
batch_size = 36 # バッチサイズの設定
torch.manual_seed(seed) # 乱数シードの固定
# 学習データセットの作成: dataloaderの作成
x_train_tensor = torch.tensor(train_X)
y_train_tensor = torch.tensor(train_y.reshape(-1, 1))
train_dataset = TensorDataset(x_train_tensor, y_train_tensor)
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True)
# テストデータセットの作成: dataloaderの作成
x_test_tensor = torch.tensor(test_X)
y_test_tensor = torch.tensor(test_y.reshape(-1, 1))
test_dataset = TensorDataset(x_test_tensor, y_test_tensor)
test_dataloader = DataLoader(test_dataset, batch_size=batch_size, shuffle=False)【実行結果】なし
2.モデルの定義
シンプルなLSTMクラスを定義します。
### LSTMモデルの定義 ★PyTorch
## LSTMクラスの定義
class LSTM(nn.Module):
def __init__(self, input_size, rnn_hidden_size):
super(LSTM, self).__init__()
self.rnn = nn.LSTM(input_size=input_size, hidden_size=rnn_hidden_size,
batch_first=True)
self.fc = nn.Linear(in_features=rnn_hidden_size, out_features=1)
def forward(self, x):
x, _ = self.rnn(x) # LSTMの出力に含まれる複数の変数からoutputを取り出し
x = self.fc(x)
return x
## モデルのインスタンス生成
torch.manual_seed(seed)
model_lstm = LSTM(input_size=train_X.shape[1], rnn_hidden_size=200)
print(model_lstm)【実行結果】

3.モデルの学習
エポック数 200 の学習を実行します。
テストデータを用いて検証します。
%%time
### NNの学習
## 乱数シード
torch.manual_seed(seed)
## 学習関数の定義
def train_nn(model, num_epochs, dataloader, loss_func, optimizer):
# 学習履歴リストの初期化
loss_history = [0] * num_epochs
# エポック数を繰り返し処理
for epoch in range(num_epochs):
# バッチ数を繰り返し処理
for x_batch, y_batch in dataloader:
pred = model(x_batch) # 1.予測値を生成
loss = loss_func(pred, y_batch) # 2.損失値を計算
loss.backward() # 3.勾配を計算(誤差逆伝播)
optimizer.step() # 4.パラメータ更新
optimizer.zero_grad() # 5.勾配の初期化
loss_history[epoch] += loss.item() # 損失値の一時格納
# 損失値を正す(バッチ数で除算)
loss_history[epoch] *= (y_batch.size(0) / len(dataloader.dataset))
# 500エポックごとに損失値を表示
if (epoch + 1) % 100 == 0:
print(f'Epoch {epoch + 1: >4}, Loss {loss.item():.2f}')
# 戻り値:学習履歴リスト
return np.array(loss_history)
## NNのパラメータなどの設定
# 学習率 テキストはおそらく0.001
learning_rate = 0.0005
# エポック数 テキストは50
num_epochs = 200
# 損失関数 平均二乗誤差
criterion = nn.MSELoss()
# 最適化手法 Adam
optimizer = torch.optim.Adam(model_nn.parameters(), lr=learning_rate)
## 学習の実行
history = train_nn(model_nn, num_epochs, dataloader, criterion, optimizer)【実行結果】

学習曲線(損失曲線)を描画します。
テキストの 図3.32(a) に相当します。
### 学習曲線の描画 ★PyTorch
plt.plot(history[0], label='train')
plt.plot(history[1], label='test')
plt.xlabel('Epoch')
plt.title('学習曲線')
plt.grid(lw=0.5)
plt.legend();【実行結果】
収束している感じがします。


予測
1.予測の実行
テストデータを用いて予測を行います。
### テストデータによる予測の実行 ★PyTorch
# 予測実行
y_pred = model_lstm(x_test_tensor).detach().numpy()【実行結果】なし
2.予測値をスケール変換
予測値を元データのスケールに戻します。
テキストオリジナルコードを一部引用いたします。
### 予測データの再スケーリング ★テキストのコードを引用、一部改変
# 変換時に必要になる説明変数の準備
test_X_add = test_X.squeeze()[:, 1:]
# yの予測データの逆変換
y_pred_inverse = np.hstack([y_pred, test_X_add])
y_pred_inverse = scaler.inverse_transform(y_pred_inverse)
y_pred_inverse = y_pred_inverse[:, 0]
# yのテストデータの逆変換
y_test_inverse = np.hstack([test_y.reshape(-1, 1), test_X_add])
y_test_inverse = scaler.inverse_transform(y_test_inverse)
y_test_inverse = y_test_inverse[:, 0]【実行結果】なし
3.残差の自己相関の確認
残差に自己相関が残っていないかの確認です。
テキストの図3.31に相当します。
### 残差の自己相関、偏自己相関プロットの描画 ★テキストと異なるコード
resid = y_test_inverse - y_pred_inverse
plot_acf_pacf(resid, lags=60)【実行結果】
残差に自己相関は見られません!

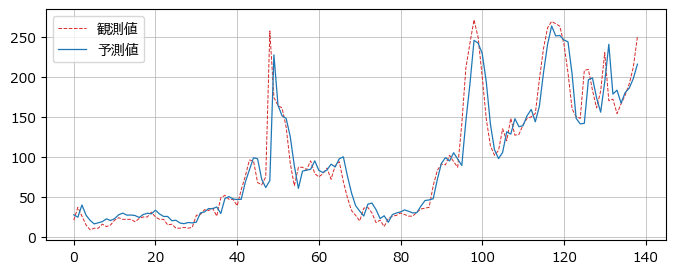
4.予測プロット
テストデータの観測値と予測値を描画します。
テキストの 図3.32(b) に相当します。
### 観測値と予測値のプロットを描画
plt.figure(figsize=(8, 3))
plt.plot(y_test_inverse, color='tab:red', lw=0.7, ls='--', label='観測値')
plt.plot(y_pred_inverse, color='tab:blue', lw=0.9, label='予測値')
plt.grid(lw=0.5)
plt.legend();【実行結果】
若干、期間の横ずれが残っています。
テキストによると「予測値は実測値とちょうど1時間ずれて形状を「複製」しています」とのこと。
今回の寄り道写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
