
分析や関係性のあれこれ
こんにちは!Dynata Marketing & PRチームです!
少しずつ秋らしくなってきましたね。
今日は分析手法についてお話ししたいと思います。
コンジョイント分析
コンジョイント分析とは、ユーザーにとって最適な商品やサービスのコンセプトを抽出すための分析手法です。マーケティングの分野で利用されています。なお、この「コンセプト」とは、商品・サービスを構成するスマートフォンでは、機能や性能、デザイン、アフターサービス、価格などの要素があげられます。そして、この要素の性能や水準を示すものが水準です。性能で言うと、CPUスペックや、メモリ・ストレージ容量、バッテリー駆動時間などが該当します。
ユーザーは、商品やサービスの購入の際に、「どの属性・水準を重視するか」という基準があり、「唯一これが決め手」という要因があるよりむしろも複雑に絡み合った属性と水準の組み合わせのなかから、自分が欲しいものを決定します。コンジョイント分析は、コンセプトの最適化を分析して、多くのユーザーに評価される商品・サービスの開発が可能とします。そのうえで、自社と他社のスペック比較によるシミュレーションも可能となります。
コンジョイント分析の進め方
A 直交表を用いて複数のコンジョイントカードを作成する
コンジョイントカードとは、効果を測定したい属性と水準を設定して作成する商品のプロファイルを言います。以下は携帯電話の例です。

属性と水準が異なる組み合わせで構成される、直交表を用いて複数のコンジョイントカードを作成します。
上記の例の場合、容量は「128か256」、防水・耐性は「強いか普通」、価格は「6万円か8万円」、というパターンがあり、全部で2×2×2の8通りの組み合わせになります。この8つから重複を整理して整理します。
B ユーザー調査の実施
作成したカードを基にしてアンケートでユーザーに評価してもらいます。複数のカードの中で、欲しいと思う順位をつけてもらう他、欲しいと思う度合いや魅力度を確認します。
仮想的な商品とは言え、具体的にスペックを前提にして点数付けまたは順位付けするため、実際の購入検討に近い前提で有効なデータを回収できます。
C 属性・水準と効用値の関連を可視化する
各属性・水準がそれぞれ、購入したい度合いにどの程度影響しているかを分析します。この分析には通常「重回帰分析」を用います。重回帰分析は、ひとつの成果(目的変数)に対して要因(説明変数)が複数あるとき、各要因がどれだけ成果に影響を与えているか分析する手法です。
コンジョイント分析では、効用値を目的変数、各属性・水準を説明変数と定義して分析を進め、影響を与えている度合いを表す数値「回帰係数」を導出します。
得られた回帰係数は、コンジョイント分析においては「部分効用」と称します。また、「欲しいと思う」水準の値はプラス、「欲しいと思わない」水準の値はマイナスで表記します。
D 部分効用を合計して評価の高い仕様を抽出
コンジョイントカードに設定した商品仕様の評価と分析結果について、各水準の部分効用値を足し合わせます。
【商品A】
0.4(256G)+0.2(防水・耐性強い) -0.75(8万円)= -1.25
【商品B】
-0.4(128G)+0.2(防水・耐性強い)+0.75(6万円)=0.55
このような計算結果が算出されました。この場合は商品Bの方が効用値が高いことから、ユーザー調査からより魅力的であると評価されます。
コンジョイント分析により最も評価の高い仕様を抽出した後、当該仕様に近づけるような製品開発を行うという手順につなげます。
相関関係と因果関係
AとBの事柄において一定の関係性があるものを「相関関係」と言い、その中でも、Aを原因としてBが変動するものを「因果関係」と言います。アンケート結果のデータだけをみると一定の関係性があると、それを「因果関係がある」と判断してしまうことも多いと思います。ここで重要なことは、「本当にこの2つの事柄に関係性はあるのか?」と凝視することです。相関関係があるからと言って、必ずしも因果関係があるわけではありません。データの裏にある人間心理や環境を考えることが重要です。
相関関係
相関関係とは、「片方の値が変化すれば、もう片方も同じように変化する関係」です。
相関関係には「正の相関」と「負の相関」があります。正の相関関係とは次の左側のグラフのように横軸の値(x)が増加すると縦軸の値(y)も増加するという関係のことです。負の相関関係とは、次の右側のグラフのようにxが増加するとyが減少するという関係のことです。下記のように散布図にして外れ値がないかも確認します。
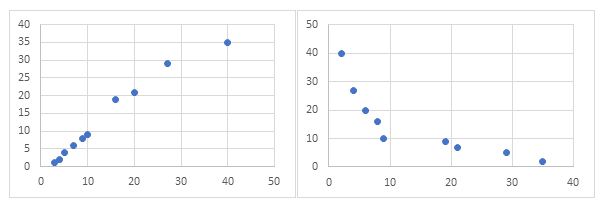
複数の変数について相関分析を用いて、相関関係があるかどうかを検証します。相関関係を定量的に評価のできる相関係数は、エクセルでもcorrel関数で簡単に算定することが可能で相関性を明らかにできます。
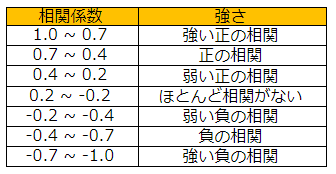
相関関係とは「Aが増加した際、Bも同じように増加する傾向にある」といった関係性のことを意味するので、
「出来事の起こる順番は関係なく」、
「お互いに影響がない可能性がある」、
「因果関係があるとは限らない」
という点に留意が必要です。
例えば、「雨が降ると来客数が減る」では「雨が降る」と「来客数が減る」という2つの事象には相関関係があると言えます。
その他にも学歴と年収。
学歴が高いと年収が高くなるイメージがありますが、高学歴が必ずしも年収が高いというわけではないので、因果関係は成立しません。
因果関係
ある事実と他の事実との間に原因と結果の関係、いいかえれば、ある事実から他の事実が引き起こされたという関係を言います。「相関関係」の中でも、原因と結果を表しているものだけが「因果関係」と言います。つまり、因果関係のあるものには相関関係がありますが、相関関係は必ずしも因果関係とはならないということです。因果関係は時間順序、直接性、相関性が成立します。他方で相関関係では、順序の関係、お互いの影響はありません。
データを読む
相関分析の結果をどのように見るのか、いくつかの視点を解説します
A 背景を考察
例えば駅前交差点で交通量と通行者の年齢層の調査を行った時「交通量が増加するのに伴って、交差点を通過する人の平均年齢が下がった」とする。結果、「交通量が増えるため、交差点を通る人の平均年齢が下がる」と言えるでしょうか。交差点は、昼頃には周辺にあるオフィス街のサラリーマンも利用しますが、夜には若者が繁華街や飲食店に向かうことが想定されます。
その結果「交通量の少ない昼の平均年齢は高くなり、交通量の増える夜には平均年齢が低くなる」と考えられます。交通量の増減が通行者の行動に影響して、結果として平均年齢を引きげているわけではないと考えられます。
B 他の要素を考える
例えば血圧と所得額の調査を行い、結果、「血圧が高い人ほど、給与水準が高かった」という相関関係が成立した場合、「血圧が高い人ほど給与が高くなる」という因果関係を導くことはできるでしょうか。他の要素を考えると、通常、年齢が高い人ほど加齢により血圧が高くなる傾向があり、一方で日本では年齢が高い人は給与が高くなる傾向にあります。そのため、データ上では血圧が高い人ほど給与水準が高くなるように見えてしまうのです。このように2つの要素以外に根本的な原因がある場合がある場合があります。因果関係を推定する際には、他の要素が影響していないかをないかを考えます。
C 周辺データを確認
例えば、複数の地域に対して電灯の数と犯罪発生件数の調査を行ったとき「電灯の数が多いほど、犯罪の発生件数は少なかった」とします。この時、調査対象外の他の地域・国での調査結果や、地域、関係者への人のヒアリング調査など周辺にあるデータをもとにして、根拠の裏付けを行い、確からしさを検証します。
と、今日は分析やデータの関係性についてお話ししました。
次回はアンケート集計のひとつ、デルファイ法についてお話ししたいと思います。
グローバル調査、ネット調査など、調査に関してはなんでも、お問合せください!(日本語で大丈夫です)
