つくば市の各地区の駅からの距離と平均年齢の関係を調べてみる

こんにちは、つくばに住む研究者です。

以前、ヒートマップ(コロプレス図)を用いてつくば市の各地区の平均年齢を色分けしてみました。これを見ると、つくばエクスプレスの駅に近い地区では、そうでない地区に比べて平均年齢がかなり低い様子が伺えます。今回の記事では、この様子をjointplotを使って数字として図示したいと思います。

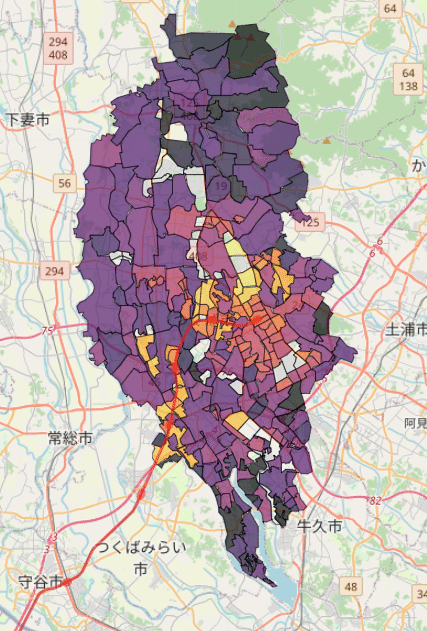
いつものように、国土地理院のデータを使います。データのダウンロード等については過去の記事を参照してください。
具体的な手順は以下の通りです。

1. 各地区(町丁目)の座標がまとめられた地理データを用意する

2. 各地区について、国勢調査結果からその地区平均年齢を紐づける

3. 駅の座標がまとめられた地理データを用意する

4. 各地区について、地域の全ての駅との距離を計算し、最寄駅までの距離を保持する

5. 最寄りまでの距離と地区の平均年齢をjointplotにまとめる

まずはそれぞれのデータを読み込みます。jointplotの作成のためにはseabornを使います。

from google.colab import drive
import pandas as pd
import numpy as  np
import matplotlib.pyplot as plt
import geopandas as gpd

import japanize_matplotlib
japanize_matplotlib.japanize()

import seaborn as sns
sns.set(font="IPAexGothic")

drive.mount('/content/drive')

まずは地区の座標データを読み込み、つくば市のデータだけを取り出します。

gdf =  gpd.read_file(files, encoding='Shift-JIS')
gdf = gdf[gdf['CITY_NAME']=='つくば市'].reset_index(drop=True)
gdf.head(3)

次に、国勢調査のデータを読み込みます。国土地理院のデータと合わせるために、地域階層レベルは2または4とします。国交省の座標データと国勢調査のデータではコードが異なるため、両者の紐付けのために、'JCODE'という列をもたせ、対応するように変換します。（このあたりはちょっと適当にやっているので、ひょっとしたら間違えているかもしれません。）

df = pd.read_csv(dir_path+'/h03_08.csv',encoding='Shift-JIS',skiprows=4)
df = df.rename({'-.1':'平均年齢'},axis=1)
df = df.rename({'-':'総年齢'},axis=1)
df = df[df['男女']=='総数']
df = df[(df['地域階層レベル']==4)|(df['地域階層レベル']==2)]
df = df[df['市区町村名']=='つくば市']
df['JCODE'] = '0'+df['市区町村コード'].astype(str).str.cat(df['町丁字コード'].astype(str))

cols= ['市区町村コード', '町丁字コード', '地域階層レベル','都道府県名', '市区町村名', '大字・町名', '字・丁目名',
'総数','0〜4歳','5〜9歳','（再掲）15歳未満','（再掲）15〜64歳', '（再掲）65歳以上', '平均年齢', 'JCODE']
df = df[cols]
df = df.reset_index(drop=True)
df.head(3)

最後に、駅のデータを読み込みます。元々のデータには全国の全ての駅が含まれていますが、今回はつくば市に関係のありそうな範囲に存在する駅のデータだけを使うことにします。

maxx = 140.25
minx = 139.8
maxy = 36.4
miny = 35.74

df_st = gpd.read_file(国土交通省の駅座標データへのパス)
df_st2 = df_st[(df_st['geometry'].bounds.minx >= minx)&
              (df_st['geometry'].bounds.maxx <= maxx)&
              (df_st['geometry'].bounds.miny >= miny)&
              (df_st['geometry'].bounds.maxy <= maxy)]

次に、各地区について平均年齢を紐付けましょう。

gdf['平均年齢']=0
for i in range(0,len(gdf)):
  try:
    gdf.loc[i, '平均年齢'] = float(df[ df['JCODE'] ==gdf.iloc[i]['KEY_CODE']]['平均年齢'])
  except ValueError:
    pass

gdf = gdf.reset_index(drop=True)

最後に、各地区の中心座標から、それぞれの駅までの距離を計算します。地球は平面ではないため、単純な緯度経度をつかって計算することが出来ないため、少し複雑な計算となります。今回はその複雑な計算を担ってくれるpyprojというライブラリを使います。

並列処理でかっこよくコードにできればよかったのですが、うまくいかなかったのでループ処理にしました。最も近い駅の名前と、2点間の距離をデータフレームのほうに持たせます。

import pyproj

grs80 = pyproj.Geod(ellps='GRS80')
gdf['station_name'] = ''

for j, rows in gdf.iterrows():
  dists = []
  for i,row in df_st2.iterrows():
    _,_, dist = grs80.inv(gdf.iloc[j]['geometry'].centroid.x, gdf.iloc[j]['geometry'].centroid.y,
                                              df_st.iloc[i]['geometry'].centroid.x, df_st.iloc[i]['geometry'].centroid.y)
    dists.append(dist)

  gdf.loc[j, 'station_name'] = df_st2['N02_005'].iloc[np.argmin(np.array(dists))]
  gdf.loc[j,'dist_from_station'] = min(dists)/1000

それでは、jointplotを使って散布図を作ります。データ点の密度をより分かりやすくするために、まずは６角タイルを使って表現してみます。

sns.set_theme(rc={'figure.dpi': 150, 'figure.figsize': (5, 5)})
sns.set(style="white", color_codes=True,font="IPAexGothic")
h = sns.jointplot(data=gdf, x=gdf['dist_from_station'], y=gdf["平均年齢"],kind="hex",ratio=4, marginal_ticks=True)
h.ax_joint.set_ylabel('地区の平均年齢(歳)', fontweight='bold')
h.ax_joint.set_xlabel('最寄駅からの距離(km)', fontweight='bold')
h.fig.suptitle("地区ごとの平均年齢と駅からの距離(つくば市)")
h.fig.subplots_adjust(top=0.95)
h.figure.tight_layout()

結果はこのようになりました。色が濃いほど、条件に当てはまる地区が多いということになります。左下から右上にかけて正の相関が伺えます。35歳以下までの平均年齢が低い地区は駅から4km以内に集中していること、また4km程度離れた地区は平均年齢が50歳程度となる地区が多いこと、6km以上離れた地区は平均年齢が高いこともわかります。この地区の住民は、サービスが集中する駅付近まで歩いて1時間程度かかることになるため、高齢化が進み自動車の運転が困難になると、日常生活に不便が出るかもしれません。将来はバスなどの公共の交通網の整備が課題になりそうです。

最後に、つくば市と同じように近年になって転入者が増加している流山市と守谷市についても同じようにjointplotを作成し、重ねてみましょう。

結果はこのようになります。

流山市も守谷市もつくば市にくらべてかなり面積が小さいことに加え、つくばエクスプレスだけでなくJRなども通っていることから、駅へのアクセスはつくば市に比べて格段によく、ほぼ全ての世帯が駅から2km以内に住んでいることがわかります。

それでは。