カオス理論

カオス理論について

カオスは、初期条件に対して非常に敏感であり、そのために長期的な予測が困難となる現象を指します
カオス理論は、非線形動力学系が示す複雑で予測困難な挙動を研究する数学的および物理的理論です。

カオス理論は、気象学、生物学、物理学、化学、社会科学、経済学など、多くの学術分野で応用されています。

カオス理論の主要な特徴

カオス理論の主要な特徴は以下の通りです。

初期条件の感度（バタフライ効果）

カオス的なシステムは、初期条件に非常に敏感であり、わずかな違いが大きな影響を及ぼすことがあります。この現象は、バタフライ効果としても知られています。

例えば「ブラジルのアマゾンでの蝶の羽ばたきが、アメリカでの竜巻を引き起こす」と表現されることがあります。

非線形動力学

カオス理論は、非線形動力学系に焦点を当てています。
非線形システムは、線形システムとは異なり、入力と出力の関係が単純ではなく、予測が困難です。

確定的カオス

カオス的なシステムは、一見ランダムに見える挙動を示すことがありますが、その背後には確定的な（決定論的な）ルールが存在しています。

つまり、カオス理論は、偶然性ではなく、システム内の非線形性が複雑さを引き起こすことを示しています。

常に発生するカオス

カオス理論は、あらゆるスケールでカオス的な挙動が存在することを示しています。つまり、いくら精度を上げても、予測不可能なカオス的挙動は避けられないことを意味します。

フラクタル

カオス理論は、フラクタル幾何学と密接に関連しています。フラクタルは、自己相似性と複雑な構造を持つ幾何学的対象であり、カオス的なシステムの挙動を視覚化するのに役立ちます。

フラクタルについては、こちらの記事で詳しく執筆しています：

決定論的モデルにおけるアタラクタとカオス

決定論的モデルでは、システムの状態が時間とともにどのように進化するかを表す一連の方程式が与えられています。このようなモデルは、初期条件に基づいて将来の状態を正確に予測することが可能です。ただし、非線形性がある場合、これらのモデルはカオス的な挙動を示すことがあります。

アトラクタとは

アトラクタとは、動力学システムが時間とともに漸近的に収束する状態や軌道のことを指します。アトラクタは、システムが一定の状態や振る舞いに落ち着く傾向があることを示します。アトラクタにはいくつかのタイプがあります。

固定点アトラクタ

システムが一定の状態に収束する場合。例えば、摩擦のある振り子は、最終的に静止状態に収束します。

限定周期アトラクタ（周期軌道）

システムが繰り返し同じ状態の系列をたどる場合。例えば、摩擦のない振り子は、周期的な往復運動を行います。

クワジ周期アトラクタ

システムが周期的であるように見えるが、実際には周期的でない場合。これは、一見周期的に見えるが、厳密には異なる軌道をたどるシステムです。

ストレンジアトラクタ

システムがカオス的な挙動を示す場合、その軌道はストレンジアトラクタに収束することがあります。ストレンジアトラクタは、フラクタル構造を持ち、非常に複雑な形状をしています。ローレンツアトラクタは、ストレンジアトラクタの一例です。

カオスは、決定論的モデルにおいて非線形性が原因で生じる複雑な挙動であり、初期条件に敏感であることが特徴です。 カオス的なシステムでは、アトラクタはストレンジアトラクタとして現れることが多く、その軌道は予測が困難でありながらも、確定的なルールに従っています。

ローレンツアタラクタ

ローレンツアトラクタは、1963年にエドワード・ローレンツが発見した、カオス理論における非常に有名なストレンジアトラクタの一例です。
ローレンツは、気象学のシンプルな数学モデルを研究していた際に、この複雑な構造を見つけました。ローレンツアトラクタは、非線形ダイナミクスとカオス理論の研究において重要な役割を果たしています。

ローレンツシステムは、3つの連立微分方程式で表される非線形動力学システムです。 ローレンツシステムは、次の3つの連立微分方程式で表されます。ここで、x、y、zは変数であり、tは時間を表します。また、σ（シグマ）、ρ（ロー）、β（ベータ）は正の定数です。

ローレンツシステムの連立微分方程式

ローレンツは、大気対流の簡略化されたモデルを研究していたときに、これらの方程式を導きました。σ、ρ、βは、それぞれ大気の物理的性質に関連するパラメータです。通常、σ = 10、ρ = 28、β = 8/3 という値が使用されることが多いですが、他のパラメータ値でもカオス的な挙動が見られることがあります。

ローレンツシステムは、非線形で連立した微分方程式のため、解析的に解くことは困難です。そのため、数値的に解く方法が一般的に用いられます。

このシステムは、初期条件に敏感であり、カオス的な挙動を示すことがよく知られています。

このシステムは、対流の簡略化されたモデルとしても知られており、その挙動は初期条件に非常に敏感です。そのため、長期的な予測が非常に困難となります。

ローレンツアトラクタは、3次元空間上に現れる複雑な軌道であり、2つの「翼」からなる形状をしています。システムの軌道は、これらの翼の間をカオティックに動き回りますが、翼の内部には決して入りません。このような挙動は、初期条件に敏感であることから、バタフライ効果として知られる現象の一例とされています。

Python code

以下のpython codeを用いることで、ローレンツアトラクタを表現できました。

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D  # 3Dプロットを行うために必要
import random

def lorenz(x, y, z, s=10, r=28, b=8/3):
    x_dt = s * (y - x)
    y_dt = x * (r - z) - y  
    z_dt = x * y - b * z
    return [x_dt, y_dt, z_dt]

dt = 0.01
xyz_ini = [0.0, 1.0, 1.05]
num_steps = 10000

xs = np.empty(num_steps)
ys = np.empty(num_steps)
zs = np.empty(num_steps)
xs[0], ys[0], zs[0] = xyz_ini  # 初期値

for i in range(1, num_steps):
    x_dt, y_dt, z_dt = lorenz(xs[i - 1], ys[i - 1], zs[i - 1])
    xs[i] = xs[i - 1] + (x_dt * dt)
    ys[i] = ys[i - 1] + (y_dt * dt)
    zs[i] = zs[i - 1] + (z_dt * dt)

# Jupyter Notebook 以外では、以下の行をコメントアウトしてください
# %matplotlib notebook

fig = plt.figure()
ax = fig.gca(projection="3d")
ax.plot(xs, ys, zs, lw=0.5)
plt.show()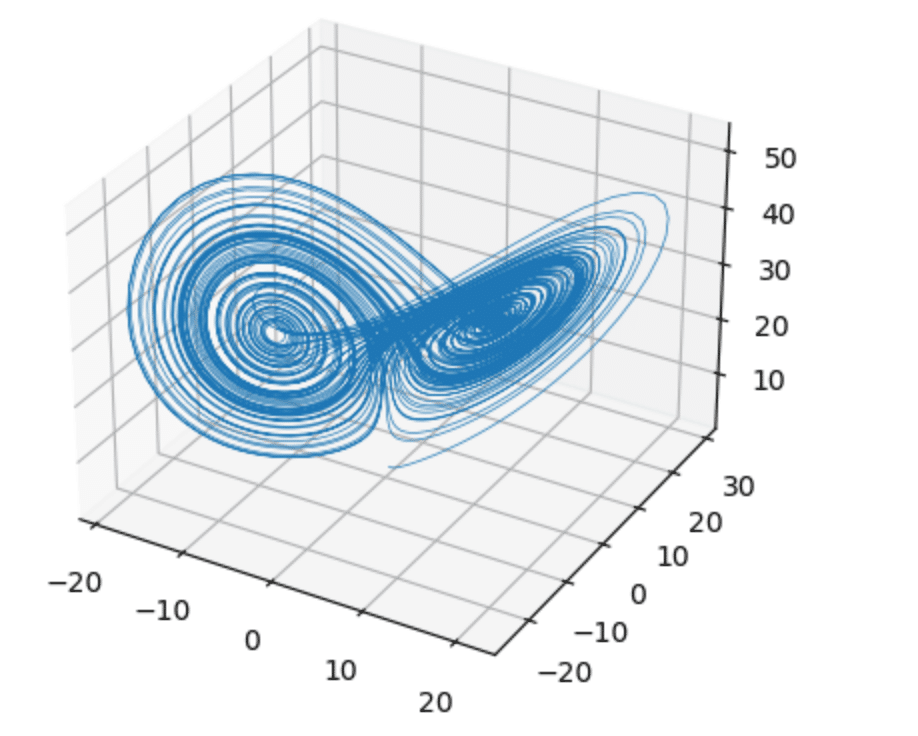  

Xの軌跡をプロットしたcodeと図は以下のとおりです

# xの軌跡をプロット
plt.figure()
plt.plot(np.arange(num_steps) * dt, xs)
plt.xlabel('Time')
plt.ylabel('x')
plt.title('x Trajectory')
plt.show()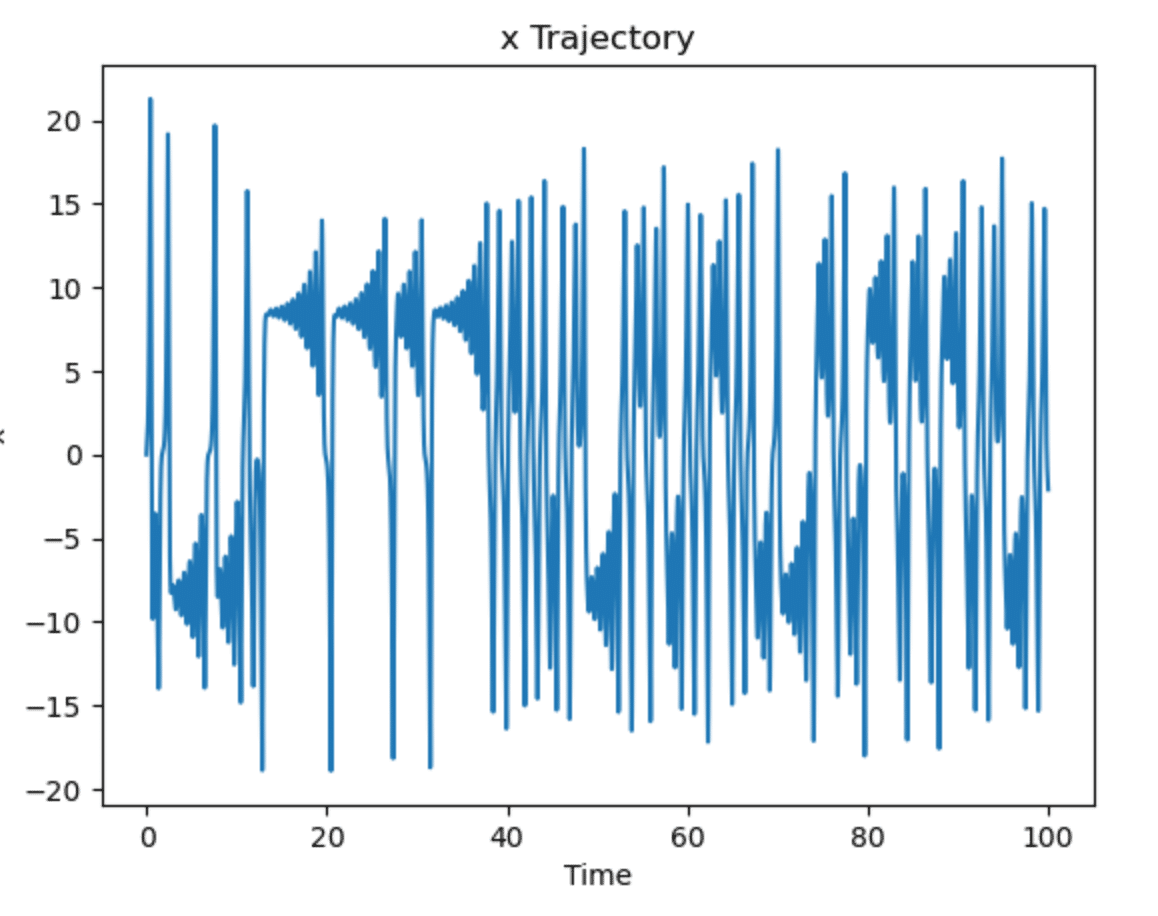

ロジスティック方程式のカオス

ロジスティック方程式は、人口動態や生物学的システムの成長を記述するために広く用いられる単純な数学モデルです。次の形式で表されます：

ここで、x(t)は時刻tにおける状態（例えば人口密度）を表し、rは成長率を示すパラメータです。x(t)は0から1の間の値をとり、1は環境の最大容量を示します。

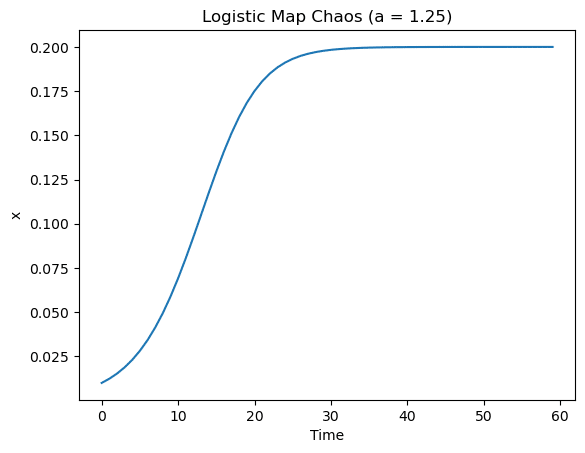
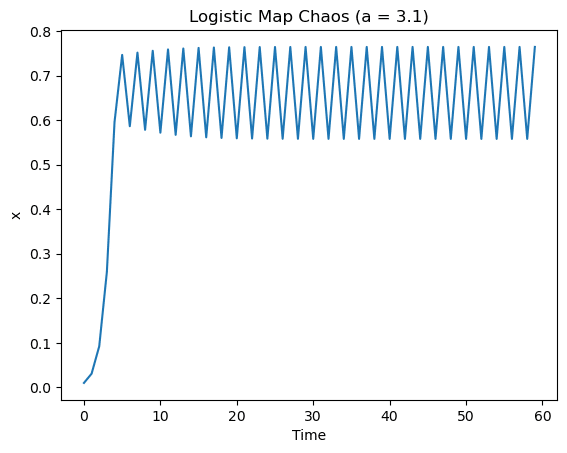
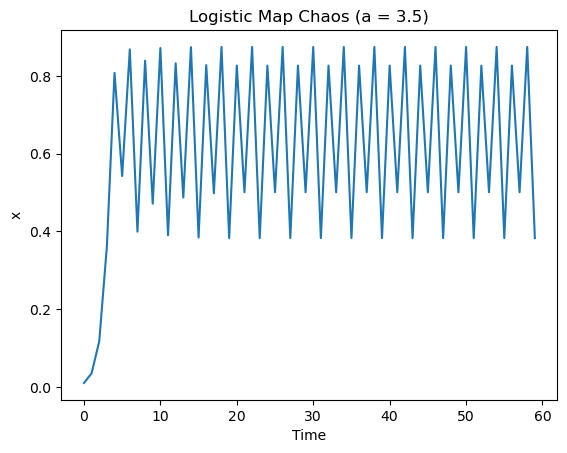
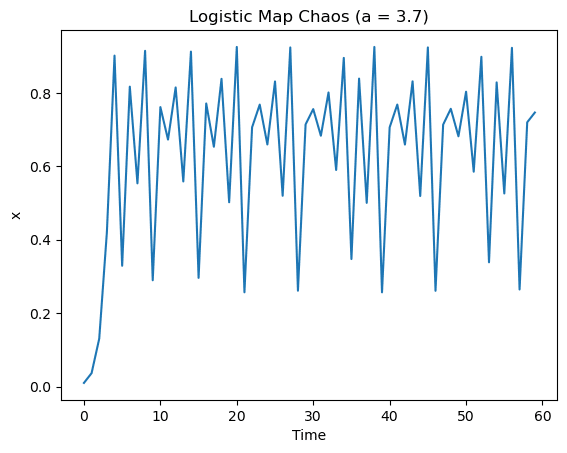
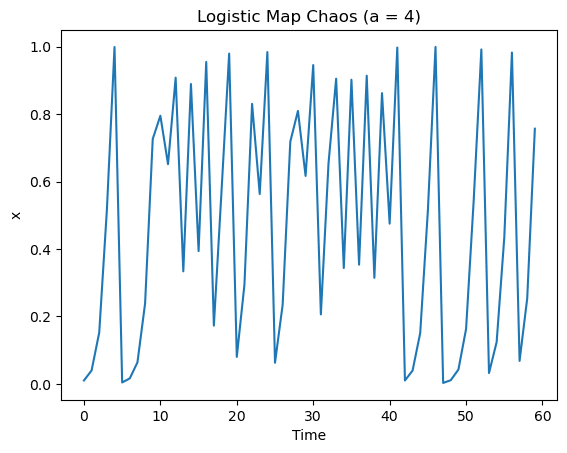
ロジスティック方程式は、rの値によって異なる振る舞いを示します。rの値が小さい場合、システムは定常状態に収束します。rが増加すると、システムは周期的振動を示すようになり、最初は2周期、次に4周期、8周期と倍になっていきます。しかし、rが約3.57を超えると、システムはカオス的な振る舞いを示すようになります。

カオスは、初期条件に対する極端な敏感さと非周期的な振る舞いを特徴とする現象です。ロジスティック方程式におけるカオスは、初期条件やパラメータの微小な変化が、時間とともに指数関数的に増大し、予測不可能な結果をもたらすことを示します。この現象は、カオス理論の基本的な例として広く研究されており、気象学、物理学、生物学など、さまざまな科学分野での応用があります。

python code

import numpy as np
import matplotlib.pyplot as plt

a_list = [1.25, 2.85, 3.1, 3.5, 3.7, 4]
num = 60
x0 = 0.01  # 初期値
xarr = np.zeros((6, num))

for i in range(6):
    xarr[i, 0] = x0
    a = a_list[i]
    for k in range(1, num):
        xarr[i, k] = a * xarr[i, k - 1] * (1 - xarr[i, k - 1])

# 結果をプロット
for i in range(6):
    plt.figure()
    plt.plot(np.arange(num), xarr[i, :])
    plt.xlabel('Time')
    plt.ylabel('x')
    plt.title(f'Logistic Map Chaos (a = {a_list[i]})')
    plt.show()

上記codeを使用すると、以下の図が作成されます

参考＆おすすめの書籍は以下：

Pythonコンピュータシミュレーション入門 人文・自然・社会科学の数理モデル