
インド式掛け算をロジック回路に応用できないか?
背景
今日の休憩中に下記の動画を見ていた
インド式掛け算はロジック回路の乗算に適用できないだろうか?
(とっくの昔に研究されたと思いますが)
インド式掛け算とは
例えば、12 x 34ですと、
最初に右の桁で2x4=8
次に斜めの1x4 + 2x3 = 10
1が桁上がりです
最後に1x3=3 に桁上がりの1を加えて4
→408
2進数では
証明を考えれば分かるとおり、2進数でも16進数でもインド式掛け算は成り立ちます。
例えば1011 (=11)x 1101(=13)ですと、
最下位ビットは1x1=1
2ビット目は1x0+1x0=0→結果は0
3ビット目は0x1+1x1+1x1=10→結果010と桁上がり1
4ビット目は1x1+0x1+1x1=10→結果は00100
5ビット目は1x1+繰り上げ1=10
→結果は全てのビットを結合して10001111 = 143 = 11x13
合ってるようです
乗算回路は
ChatGPTより
module vedic_4bit_multiplier (
input [3:0] A, // 4-bit input A
input [3:0] B, // 4-bit input B
output [7:0] P // 8-bit output P (Product)
);
wire p0, p1, p2, p3, p4, p5, p6, p7;
wire carry1, carry2, carry3, carry4, carry5;
// 1-bit partial products
assign p0 = A[0] & B[0];
assign p1 = (A[1] & B[0]) ^ (A[0] & B[1]);
assign carry1 = (A[1] & B[0]) & (A[0] & B[1]);
assign p2 = (A[2] & B[0]) ^ (A[1] & B[1]) ^ (A[0] & B[2]);
assign carry2 = ((A[2] & B[0]) & (A[1] & B[1])) | ((A[1] & B[1]) & (A[0] & B[2])) | ((A[2] & B[0]) & (A[0] & B[2]));
assign p3 = (A[3] & B[0]) ^ (A[2] & B[1]) ^ (A[1] & B[2]) ^ (A[0] & B[3]);
assign carry3 = ((A[3] & B[0]) & (A[2] & B[1])) | ((A[2] & B[1]) & (A[1] & B[2])) | ((A[1] & B[2]) & (A[0] & B[3])) | ((A[3] & B[0]) & (A[1] & B[2])) | ((A[2] & B[1]) & (A[0] & B[3]));
assign p4 = (A[3] & B[1]) ^ (A[2] & B[2]) ^ (A[1] & B[3]) ^ carry1;
assign carry4 = ((A[3] & B[1]) & (A[2] & B[2])) | ((A[2] & B[2]) & (A[1] & B[3])) | ((A[1] & B[3]) & carry1) | ((A[3] & B[1]) & (A[1] & B[3])) | ((A[2] & B[2]) & carry1);
assign p5 = (A[3] & B[2]) ^ (A[2] & B[3]) ^ carry2;
assign carry5 = ((A[3] & B[2]) & (A[2] & B[3])) | ((A[3] & B[2]) & carry2) | ((A[2] & B[3]) & carry2);
assign p6 = (A[3] & B[3]) ^ carry3;
assign carry6 = (A[3] & B[3]) & carry3;
assign p7 = carry4 ^ carry5 ^ carry6;
// Assign to output
assign P[0] = p0;
assign P[1] = p1;
assign P[2] = p2;
assign P[3] = p3;
assign P[4] = p4;
assign P[5] = p5;
assign P[6] = p6;
assign P[7] = p7;
endmoduleこれは4bit x 4bitです
(後でテストしましたが、この回路では全てのbitの組み合わせでは計算が合いません)
8bitでは
module vedic_8bit_multiplier (
input [7:0] A, // 8-bit input A
input [7:0] B, // 8-bit input B
output [15:0] P // 16-bit output P (Product)
);
wire [7:0] P0, P1, P2, P3;
wire [11:0] S1, S2;
wire carry1, carry2;
// Instantiate 4-bit Vedic Multipliers
vedic_4bit_multiplier M1 (.A(A[3:0]), .B(B[3:0]), .P(P0)); // A[3:0] * B[3:0]
vedic_4bit_multiplier M2 (.A(A[7:4]), .B(B[3:0]), .P(P1)); // A[7:4] * B[3:0]
vedic_4bit_multiplier M3 (.A(A[3:0]), .B(B[7:4]), .P(P2)); // A[3:0] * B[7:4]
vedic_4bit_multiplier M4 (.A(A[7:4]), .B(B[7:4]), .P(P3)); // A[7:4] * B[7:4]
// Add partial products
assign {carry1, S1} = {4'b0000, P1} + {P2, 4'b0000}; // Middle 12 bits
assign {carry2, S2} = {P3, 8'b00000000} + {4'b0000, carry1, S1[11:4]};
// Final product
assign P[3:0] = P0[3:0]; // Least significant 4 bits
assign P[11:4] = S1[7:0]; // Middle 8 bits
assign P[15:12] = S2[11:8]; // Most significant 4 bits
endmodule
4ビット毎にインド式掛け算をやっていく。
どんどん回路を積み重ねていけばいいわけです。
考察
ええと、見た感じ、ビット幅が増えるとメリット無くなるよね?とChatGPTに聞いたら、
その通りだそうです。ワラスツリーでしたっけ?
所感
20代の時に先輩社員に
「俺が若手の時は乗算機をトランジスタ手書き(レイアウト設計)して20代が終わった・・・」(略)
と聞いたとこがあったのですが、
今は、CADでAxBとかけばAxBの乗算機が生成されるわけです。
(中身はFPGAベンダーしか知り得ない)
では、どうするか?
過去の記事でAIとは膨大な乗算計算を繰り返し行くことが分かりました。そしてAIでは精度はそれほど必要ないはず。GPUは基本単精度。
さらにニューロンからニューロンへの変換カーブの演算に精度を落とせる領域があるはずです。(下のビット出力は乱数でも入れたら?)
また、順伝播と逆伝播の計算で必要な精度も変わってきそうです。
インド式乗算回路は、再構成可能な回路設計となっていますから、これにより動的にビット幅や計算精度を動的に調整できるでしょうね。
参考
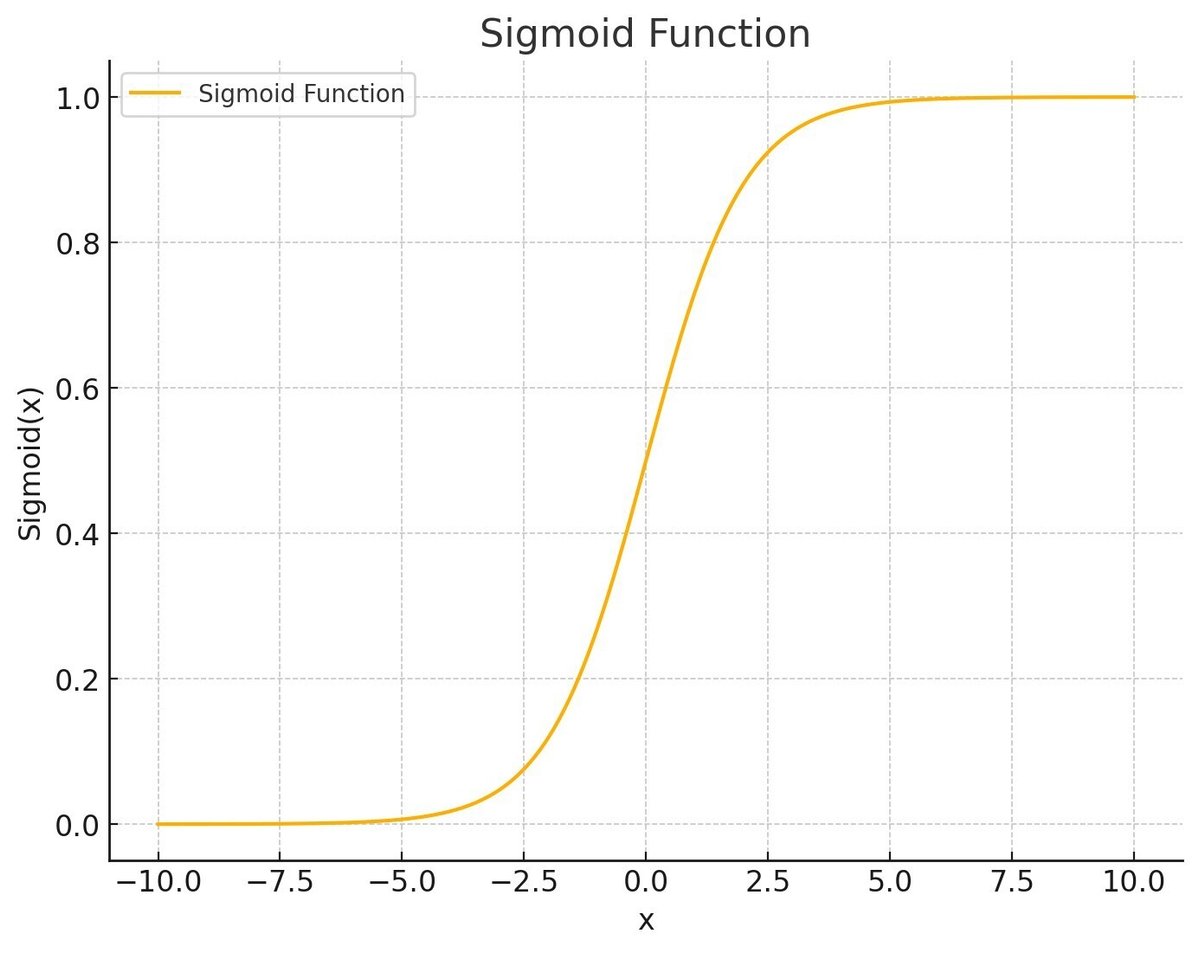
これがニューラルネットワークで使われてたシグモイド関数というもの。上下の部分はバッサリ計算精度は落とせそうですよね。今のディープラーニングはLeRU関数を使うそうですが、それもニューロンの出力と重みのテーブルの特定の領域の中で計算精度は落とせるのでは?
ということで、再度、消費電力や面積回路規模の面でインド式掛け算を応用したAI演算向けの専用乗算回路を設計するのも(とっくに枯れたロジック設計業界で)面白そうですね。
