CATE を推定する Uplift Modeling の概要
アップリフトモデリングについていくつか書籍と論文に目を通して勉強しました。興味のある箇所をピックアップしてメモします。
Uplift Modeling の概要
Uplift Modeling は ATE や ATT よりもっと細かくサブグループ、ないしは個人ごとの因果効果を推定する手法です。これは Conditional Average Treatment Effect, CATE を推定することと言い換えることができます。ある個人 $${i}$$ の treatment を受けた場合の outcome を $${Y_{i}(1)}$$, そうでなかった場合の outcome を $${{Y_{i}(0)}}$$, 因果効果を $${\tau_{i}}$$ と表記すると CATE は次の式で表されます。
$$
CATE: \tau\left(X_i\right)=E\left[Y_i(1) \mid X_i\right]-E\left[Y_i(0) \mid X_i\right]
$$
Uplift Modeling の有用性
ABテストや観察データでの因果推論の手法では、介入が集団単位でどのような効果があるかの因果を推定することができますが、あくまでわかるのは集団レベルの話です。効果があるとされる集団の中でも、効果がなかった個人は存在し得ます。
この差が重要になるのは、例えばキャンペーンを行う場合などです。集団全体に対してキャンペーンを行なってしまうとその効果に応じて次の 4 パターンが存在します。
Sure Things: キャンペーンがなくとも Positive な行動をとる
Persuadable: キャンペーンがあることで、Positive な行動をとる
Lost Causes: キャンペーンがあったとしても positive な行動を取らない
Do Not Disturbs: キャンペーンがあるせいで、positive な行動を取らない
キャンペーンのROIを最大化することを考えると、これら 4 パターンのセグメントのうち「Persuadable」のセグメントに対してのみキャンペーンを行うことが望ましいことがわかります。集団を対象とした効果があると仮にABテストでわかったとしても、その集団の中にはばらつきがありキャンペーン効果のない人物や、逆にキャンペーンがネガティブに作用してしまう人物も存在し得ます。Uplift Modeling でより精緻にターゲティングを行うことが可能となります。
Approach
[1] での分類に則ってたくさんあるアプローチをメモします。なお、Two-Model Approach と Class Transformation Method については python の scikit-uplift パッケージでの実装が便利そうです。
Two-Model Approach
Two-Model Approach は名前の通り 2 つの予測モデルを作るアプローチで、しばしば uplift modeling においてはベースラインモデルとして使用されるそうです。具体的には下記を行います。
treatment group のデータを用いて $${ E[Y_i(1) | X_i] }$$ を、control group のデータを用いて $${E[Y_i(0)|X_i] }$$ をモデリング
2 つのモデルから得られる予測値の差分を uplift とする
この方法の良い点は simple であることで、各々のモデリングには Random Forest や XGBoost などさまざまな機械学習アルゴリズムを用いることができます。([2] ではロジスティック回帰でのハンズオンが乗っています。)
ただし、ベースラインモデルとして使用される、とあるように概して他のアプローチよりも劣る場合が多いそうです。[1] ではその 1 つの理由として、個別にアウトカムを予測しているため弱いアップリフトのシグナルを見落としうると指摘されています。
[2] では、改良として Interaction Model が紹介されています。Interation Model はその名前の通り交互作用項を加えて 1 つのモデルで推定するアプローチです。説明変数を $${X_i}$$, $${W_i}$$ は介入の有無を表す 01 のバイナリ変数とすると
$$
Y_i = \text{intercept} + a X_i + b W_i + c X_i W_i
$$
このように介入と説明変数の交互作用項を持たせたモデルを組みます。この時に係数 $${b}$$ は介入が行われたこと自体の主効果であり、$${c}$$ が介入があったことでの説明変数の増分効果となります。
The Class Transformation Method
Class Transformation Method では outcome を次のように変換します。なお、$${Y_i^{obs} = \{0, 1\}}$$ であることが前提となります。
$$
Z_i=Y_i^{o b s} W_i+\left(1-Y_i^{o b s}\right)\left(1-W_i\right)
$$
この変換で得られる $${Z_i}$$ は、treatment group に属していて実際に介入を受けた場合には $${Z_i = Y_i^{o b s} = 1}$$ となり、control group に足していて実際に介入を受けなかった場合にも $${Z_i = 1 - Y_i^{o b s} = 1}$$となり、反実仮想の状況では 0 となります。
このとき outcome がA/Bテストで得られた前提のもとで、次の式変形を得られます。(詳細は [3] を参照)
$$
\tau\left(X_i\right)=2 P\left(Z_i=1 \mid X_i\right)-1
$$
よって、変換した $${Z}$$ を目的変数としたモデルを構築した上で、予測値について上記のように計算すれば uplift を求められることになります。
一方で、A/Bテストが行えず観察データから求める必要がある際には上記は使用できず、傾向スコア $${\hat{p}\left(X_i\right)}$$ を用いて次のように変換します。
$$
Y_i^*=Y_i(1) \frac{W_i}{\hat{p}\left(X_i\right)}-Y_i(0) \frac{\left(1-W_i\right)}{\left(1-\hat{p}\left(X_i\right)\right)}
$$
介入を受けた場合($${W_i = 1}$$)には、$${Y_i^*=Y_i(1) \frac{1}{\hat{p}\left(X_i\right)}}$$, 受けなかった場合($${W_i = 0}$$)には、$${Y_i^*=Y_i(0) \frac{1}{1- \hat{p}\left(X_i\right)}}$$ と、元のアウトカムを傾向スコアの逆数で補正していることがわかります。もし傾向スコアの元で条件付き独立の仮定が成立していれば、この補正により共変量バランスがとれたことになり、 $${X_i}$$ で条件つけた $${Y_i^*}$$ の期待値は CATE となります。
$$
E\left[Y_i^* \mid X_i\right]=\tau\left(X_i\right)
$$
Modeling Uplift Directry
このアプローチでは、Uplift を直接予測できるように既存の機械学習アルゴリズムに修正をかけます。K近傍法やSVMなどさまざまなモデルを対応させる試みがあるそうですが、[1] では Tree Base のモデルが紹介されていました。
既存の Tree base のモデルはジニ不純度や、エントロピーに基づく情報利得を木の分割基準としていますが、次のように treatment, control ごとの outcome の分布間距離を、分割前と後でどれくらい減少できるかを分割基準とするような修正が行われます。
$$
\Delta_{\text{gain}} = D_{\text{after-split}}(P^T, P^C) - D_{\text{before-split }}(P^T, P^C)
$$
上記で $${P^T}$$ は treatment group における outcome の分布, $${P^C}$$ は control group における outcome の分布を表します。$${D(.)}$$ は距離指標を表しており、具体的には次で定義される、KLダイバージェンス, ユークリッド距離, カイ二乗距離が提案されています。
$$
\begin{align*}
KL(P: Q) &=\sum_{k=\text { Left }, \text { Right }} p_k \log \frac{p_k}{q_k} \\
E(P: Q) &=\sum_{k=\text { Left }, \text { Right }}\left(p_k-q_k\right)^2 \\
\chi^2(P: Q) &=\sum_{k=\text { Left }, \text { Right }} \frac{\left(p_k-q_k\right)^2}{q_k}
\end{align*}
$$
なお通常の決定木と同様、バギングでオーバーフィッティングしやすい問題を解決しようとするアプローチがあり、そちらは Causal Forest や Uplift Forest と呼ばれます。
Evaluation
uplift model はどのように評価すればよいでしょうか?もし反実仮想のデータが手に入れば、uplift の予測値と真値の差分などが使えそうですが、残念ながら真値は観測することができません。そこで uplift model の評価は Uplift Curve や Qini Curve が一般的に用いられそうです。
Uplfit Curve
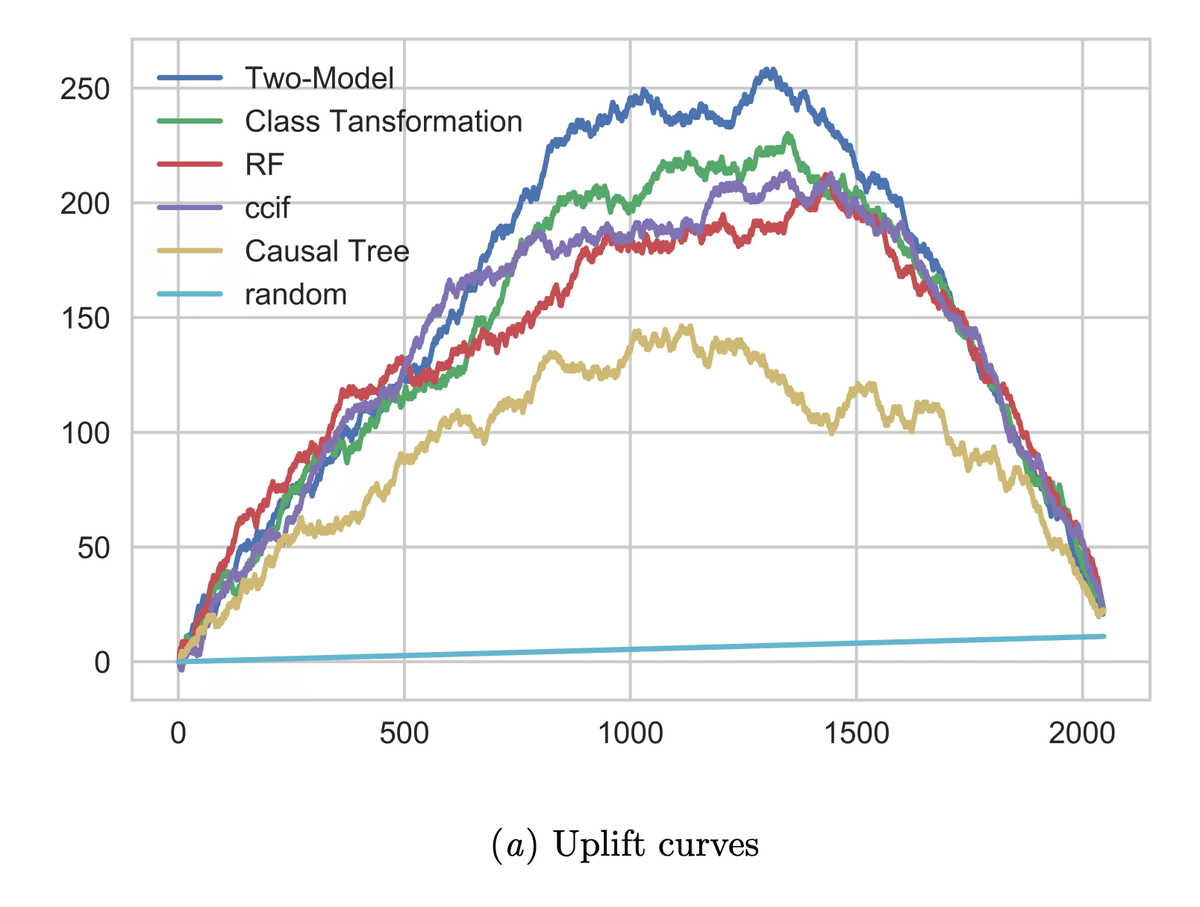
Uplift Curve は次で定義されます。予測アップリフト値を降順に並び替えたときに上から $${t}$$ サンプルを対象としたときに、 $${Y^T_t}$$ は Treatment Group における outcome の合計, $${Y^C_t}$$ は Control Group における outcome の合計, $${N^T_t}$$ は Treatment Group のサンプルサイズ, $${N^C_t}$$ は Control Group におけるサンプルサイズを意味します。
$$
f(t)=\left(\frac{Y_t^T}{N_t^T}-\frac{Y_t^C}{N_t^C}\right)\left(N_t^T+N_t^C\right)
$$
$${\frac{Y_t^T}{N_t^T}}$$ は(予測 uplift が大きい top t サンプルにおける)Treatment Group の outcome の平均値, $${\frac{Y_t^C}{N_t^C}}$$ は Control Group の outcome の平均値を表すことになるので、平均的な介入効果を人数分かけ合わせた合計の効果を表していることがわかります。
介入効果が大きいほど曲線下の面積は大きくなるため、複数の uplift model を比較する際にはそれを比較基準とすることができます。また、Curve の頂点の部分が最も介入効果が大きくなる部分となるため、予測 uplift の top 何人に対してまで介入すべきか、という示唆も得られます。
Qini Curve

Qini Curve は Uplift Curve とよく似たもので、次で定義されます。
$$
g(t)=Y_t^T-\frac{Y_t^C N_t^T}{N_t^C}
$$
こちらは Treatment Group の outcome の合計と、Control Group の outcome の平均($${\frac{Y_t^C}{N_t^C}}$$)を Treatment Group のサンプルサイズ($${N_t^T}$$)分合計したものの差分となっています。
Uplift Curve も Qini Curve も top t 人に対してどれだけの介入効果が得られるかを計算した値ですね。
なお、[4] では Uplift Modeling が Sure Things(キャンペーンがなくとも Positive な行動をとる)のセグメントをキャンペーン対象から除外できることを重要視した上で、Qini Curve ではどれくらい Sure Things を排除できているか把握できない課題を指摘し、Sure Things 曲線(ST曲線)で評価することを提案しています。
おわりに
データを価値に変える事を考えたときに、データを分析して改善の示唆を出す、みたいなことは場合によっては時間をかけても期待するほどの示唆が得られないこともありますが、Uplift Modeling はわかりやすく効果が得られるアプローチなため取り組みやすそうです。仕事でも機会があったらぜひ取り組んでみたい内容でした。
Reference
[1] Pierre Gutierrez, Jean-Yves Gérardy. Causal Inference and Uplift Modeling: A Review of the Literature, 2017
[2] Joanne Rodrigues. Product Analytics: Applied Data Science Techniques for Actionable Consumer Insights, 2020
[3] Maciej Jaskowski and Szymon Jaroszewicz. Uplift modeling for clinical trial data, 2012
[4] 清水 亮洋, 富樫 陸. クーポンマーケティングにおけるUplift Modeling適用の問題点と新しい評価指標, 2020
[5] scikit-uplift documentation
最後まで目を通していただきありがとうございました。もし内容に誤りを見つけていただいた場合はご指摘いただけますと幸いです🙇♂️
ここから先は
¥ 100
この記事が気に入ったらサポートをしてみませんか?
