Defiを理解しようシリーズ　第5回： 小学生でもわかるUniswap v3とCurve

「UniswapとCurve、どちらがDefiの中心なのか」

という論争が最近あるらしいです。

自分の意見としては「どっちも」なのですが、とりあえずuniswapが開発した、下記の有名なAMMの等式はとても美しいと思います。

$$
x * y = k
$$

ただ、このv2の等式は有名な反面、v3の等式が頭に入ってる人は少ないかと思います。

そしてUniswap v3というのは、実はCurveのStable Swapとよく似ているのです。

今回は、（高校程度の数学を理解している）小学生でもわかるようにuniswap v3の等式を導出、Curve Stable Swapとの類似性を解説していこうと思います。

基本的な考え方

CurveのStable Swap

まず第一回を熟読してください。

Uniswap v3の考え

Uniswap v3の基本的な考え方は、集中流動性と呼ばれるものです。

v2の$${x * y = k}$$は、とてもシンプルであり、すべてのpriceの範囲（0, ∞）で動作します。

しかし言い換えればそれはとても資本効率が悪いものになります。

なぜなら、priceが(a,b)の範囲内で動くとすると、ほとんどの範囲の流動性が触られることなく流動性プールの中に眠ってしまうからです。

そこでv3では「ある価格帯以外はカットした」流動性を考えました。white paperではvirtual reservesと呼ばれています。

このvirtual reservesでは(a,b)の価格帯でしか流動性を提供しません。
そうすることによって、流動性を価格帯(a,b)に集中することができます。

しかし集中することができる反面、価格帯(a,b)からはずれると流動性がなくなります。

v3では1つの通貨ペアに対して複数の流動性プールを持たせることでこの問題を解決しました。

v2では1つの通貨ペアに対して1つのプールでしたが、v3では１つの通貨ペアに対して価格帯ごとに複数のプールを持たせることが可能です。

従って、下記の図のように、一つのプールで価格帯をはずれたとしても、別のプールの流動性によって通貨の交換がカバーされます。

この価格帯は流動性提供者が決めることができます。
なので、トークンの価格の変化に従って、流動性提供者はプールを抜き差ししながら価格帯を変えたプールを作成するでしょう。

それによって市場原理に基づいた合理的なプールの生成がなされることが期待されています。

v2とv3ではLPトークンの実装にも違いがあります。

v3のLPトークンは、流動性プールごとに価格帯やfeeなどのプロパティを持つ必要があるため、単一のERC20トークンで表すことができません。
そのため、NFTの規格であるERC-721で表現されます。
これはwhite paperではNon-Fungible Liquidityと呼ばれています。

まずは、Curve Stable Swapと比較するためにこのUniswap v3で使われる集中流動性の式を求めてみます。

v3の式を求めてみる

数学に長けた人ならわかるだろうけど

uniswapのWhite Paperを読むと、以下のように書いてあります。

The amount of liquidity provided can be measured by the value
𝐿, which is equal to √𝑘. The real reserves of a position are described
by the curve:  (2.2)

This curve is a translation of formula 2.1 such that the position is solvent exactly within its range (Fig. 2).

Curve white paper: https://uniswap.org/whitepaper-v3.pdf

式2.2

$$
(x + \frac {L}{\sqrt p_b} )( y + L \sqrt {p_a}) = L ^2
$$

Fig 2

前述したように、Uniswap v2をある価格帯以外をカットしたものがUniswap v3の式です。

しかし、white paperには「～なのでこうなります」と唐突に式がかかれているだけで、導出の過程は書かれていません。

数学に長けた人ならば、数式だけで理解できるかもしれませんが、大抵の方はいきなり数式を出せれても意味が解らないかと思います。

なので、もう少しv3の式の導出の過程を解説してみたいと思います。

もうちょっと式の導出の過程を

下記のように、シンプルにv2の曲線をshiftさせたものがv3であることがわかります。

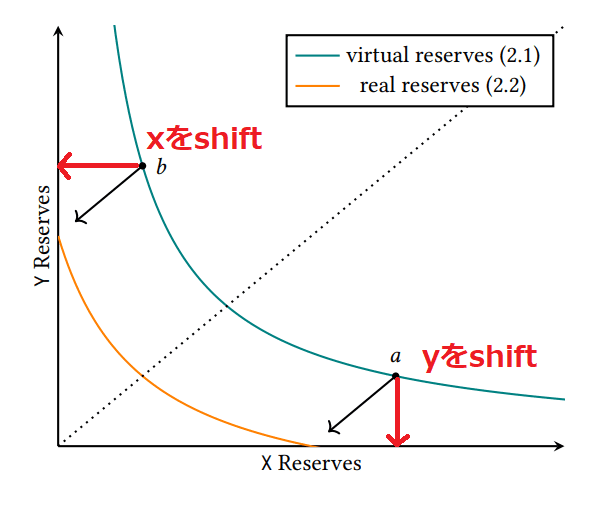
$${y = f(x)}$$を$${(-x_b, -y_a)}$$シフトした場合の$${f_a(x)}$$は

$$
y + y_a = f_a(x + x_b)
$$

となります。

つまりuniswap v3の式を表すと、

$$
(x + x_b)(y+y_a) = k
$$

となります。

なので、uniswap v2をどれだけシフトすればよいかの、$${x_b}$$ $${y_a}$$を求めれば、v3の式が導出できます。

グラフから$${x_b}$$は点bでのx座標であり、$${y_a}$$は点aのy座標であることがわかるかと思います。

ここで、priceは在庫関数の微分値である、ということを思い出しましょう。(第1回を読んでる前提）

つまり、点bのx座標とは、$${dy/dx = p_b}$$となるxであり
点aのy座標とは、$${dy/dx = p_a}$$となるyとなります。

v2の式から$${dy/dx}$$を求めると

$$
\frac {dy} {dx} = - \frac {k} {x^2} 
$$

点bでの$${-dy/dx}$$がprice $${p_b}$$となるので、

$$
- \frac {dy} {dx}  = p_b = \frac {k} {x_b^2} 
$$

これを$${x_b > 0 }$$で解いて、

$$
x_b = \frac {\sqrt k} {\sqrt P_b}
$$

となります。

また、同様に、v2の式から$${dx/dy}$$を求めると

$$
\frac {dx} {dy} = - \frac {k} {y^2} 
$$

当然ですが、xとyを逆転したものになります。

点aでの$${-dx/dy}$$がprice $${\frac {1}{p_a}}$$となるので、

$$
- \frac {dx} {dy}  = \frac {1}{p_b} = \frac {k} {y_a^2} 
$$

これを解いて、

$$
y_a = {\sqrt k}   {\sqrt p_a} 
$$

ここで、$${x_b}$$ $${y_a}$$が求まったので、式に代入し、 $${{\sqrt k}=L}$$と置きます。

$$
(x + \frac {L}{\sqrt p_b} )( y + L \sqrt {p_a}) = L ^2
$$

となり、求めるv3の式が得られました。

Curve Stable Swapとの違いは？

「USDT-USDCの集中流動性プールをUniswap v3で組む」
「USDT-USDCの流動性プールをCurve Stable Swapで組む」
これらの違いははたして何でしょうか？

同じ変化量でpriceレンジを組む

CurveのStable Swapと比較するために、USDT-USDCのような価格が1.0の状態のプールを考えましょう。
中心(price 1.0)から同じ変化量の価格レンジで流動性を組みます。

同じ変化量なのでa地点とb地点のpriceは逆数の関係となります。
つまり、$${p = p_a = 1/p_b}$$です。

従って、v3の式は

$$
(x +L \sqrt {p})( y + L \sqrt {p}) = L ^2
$$

となります。

展開して比較する

これを展開してみましょう。

$$
L\sqrt {p}(x +y) + xy = L^2 (1 - p)
$$

この数式を見て気づいた方は鋭い。

第一回で出てきた、下記のUniswapの式とConstant Swapの式を足し合わせた式にとてもそっくりですね。

$$
\lambda D(x + y) + xy = \lambda D^2 + (\frac {D} {2})^2
$$

第一回よりグラフ

この二つのv3とCurveの式から

$$
\lambda D = L \sqrt{P}
$$

$$
\lambda D^2 + (\frac {D} {2})^2 = L^2 (1 - p)
$$

が成り立つとすると、

$$
L=D (\lambda + \frac {1}{2})
$$

$$
P = (\frac {\lambda} {\lambda+1/2})^2
$$

が導かれます。

これは、CurveのStable Swapは$${L=D (\lambda + \frac {1}{2})}$$、レンジの下限価格$${ (\frac {\lambda} {\lambda+1/2})^2}$$をもつuniswap v3の式と同じであるということを意味しています。

つまり、uniswap v3とCurve Stable Swapはほぼ同義のことをやっているのです。

しかしこのままでは在庫が枯渇してしまう問題が発生します。

Curve Stable Swapでは、ここからさらにプールの量が均衡している時は定数、プールの量が偏るにつれて0となる動的レバレッジを導入することにより問題を解決しました。

一方Uniswap v3では、流動性提供者によって指定された複数のpriceレンジの流動性プールを用意することによって対応しました。

仕組みの違いはあれども、「レバレッジをかけた流動性プール」という意味では同義なのです。

いかがでしたでしょうか！

いきなり数式を出されても？？ですが、順を追って行けば理解できたかな、と思います。

Uniswap v3とCurve Stable swapは、まったく違うことをやっているようで、実は数学的には非常に似たことをやっているという、面白いことがわかったと思います。

次はみんな大好きインパーマネント・ロスの話でもしようかなと思います。（この記事に追加予定だったが、長くなりそうだったのでカットした）