
[妄想] 反物質の対消滅(Annihilation)(3)
量子力学視点で、陽子1個と反陽子1個の2体問題を考えたら、水素原子と同じで、互いに、引き合うとしても、簡単には、対消滅はしないですよね。 対消滅を発生させるためには、積極的に、それらを加速器で衝突させる必要がありそうに思えるのよね。 そもそも対消滅の仕組みが未知ですね。 Delusion) If you think about the two-body problem of one proton and one antiproton from the viewpoint of quantum mechanics, it is the same as a hydrogen atom, and even if they attract each other, they do not easily annihilate. In order to generate annihilation, it seems necessary to aggressively collide them with an accelerator. In the first place, the mechanism of annihilation is unknown.
しかし、陽子1個と反陽子1個で、電子をまとわず。水素の様に存在する原子?は、なんって言うんだろうか?(準粒子と言うらしい)
However, one proton and one antiproton do not wear electrons. Atoms that exist like hydrogen? What do you say? (It seems that it is called a quasiparticle)
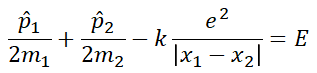
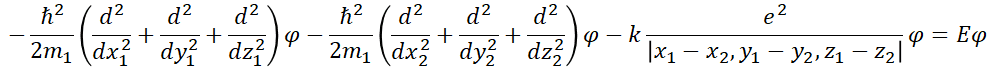
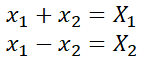
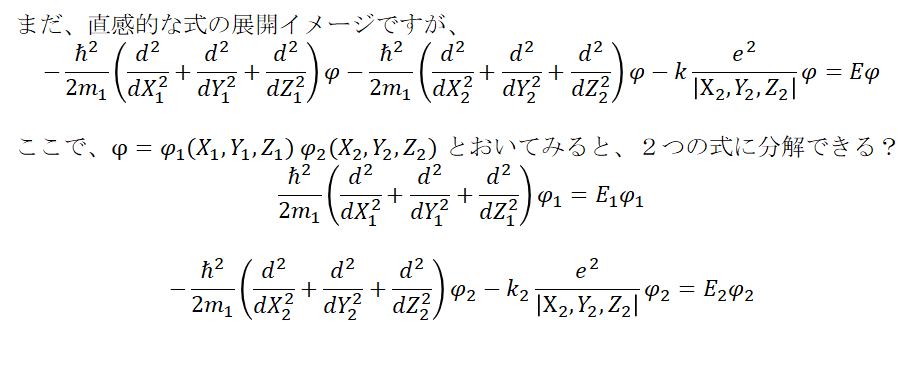
自由運動の式と、水素の電子運動と同じような式とに分解されるようにイメージしています。この式の分解が正しければ、解も解けそうですね。 It may be a little confusing, but I imagine it to be decomposed into a formula of free motion and a formula similar to the electron motion of hydrogen. If the decomposition of this equation is correct, it seems that the solution can be solved.
水素の基底状態の解(球体)と同様になるとすると、波動関数は、横長の楕球体になりそうな予感しますね。 電磁場の影響を受けて電離するような粒子で、電場に対して、双極子の性質がありそうです。また、パウリの排他律、電子スピンもあるので、↑↑、↑↓、↓↓の状態を持つのかな。電磁場と相互作用することを考えると、ダークマターとは異なる性質ですね。ただ、対発生の現象は、この謎な物質に、光子が当たることで、反物質と、物質に、電離しますね。 <P+,P->, <e+, e->のクーロン力場での対は、存在できるのかどうか?
If it is similar to the solution (sphere) of the ground state of hydrogen, the wave function seems to be a horizontally long elliptical sphere.
It is a particle that is ionized under the influence of an electromagnetic field, and seems to have dipole properties with respect to the electric field.
Also, due to Pauli exclusion principle, electrons also have spins, so I wonder if they have the states of ↑↑, ↑↓, ↓↓.
Considering that it interacts with electromagnetic fields, it has different properties from dark matter.
However, the phenomenon of pair generation is that when a photon hits this mysterious substance, it ionizes into the antimatter and the substance. Can a pair of <P +, P->, <e +, e-> in the Coulomb force field exist?
<P+,P->の波動関数の場合も、球体になる予想してます。この際、P+とP-は、核融合しないのかどうかが気になるところです。核融合が起きたとすると、構成要素とのペアーに細分化される可能性が高く、空間から消滅するということは、考えにくいのです。また、量子力学の不確実性の関係から、無になる解は許されないという前提があります。
In the case of the wave function of <P +, P->, we expect it to be a sphere.
At this time, I am wondering if P + and P- will not undergo nuclear fusion.
If fusion occurs, it is likely to be subdivided into pairs with components, and it is unlikely that it will disappear from space.
In addition, there is a premise that a solution that becomes nothing is not allowed due to the uncertainty of quantum mechanics.
話を簡単にするために、不可分なレプトンである電子と陽電子に絞って、考えます。
To keep things simple, let's focus on the indivisible leptons, electrons and positrons.
電子と反電子で考えると、陽子が、だいぶん軽い反電子に入れ替わるので、基底状態の半径は、だいぶん大きくなると予想できます。 コトバンクによると、陽子の質量は1.6726×10-24gで、電子の約1836倍なので、<e+,e->の球体の半径は、水素原子とく比べて、いぶん大きなものになると思います。 水素原子の大きさが、約1nmなので、陽子との質量比の逆数に比例するとすれば、おおよそ2µm(PM0.2粒子)になる。これは、準物質っていう分るかな? 電子は、不可分な素粒子なので、これが、本当に、AS-ISで存在するのかどうか? In terms of electron and anti-electrons, it can be expected that the radius of the ground state will be much larger because the protons will be replaced by much lighter anti-electrons. According to Kotobank, the mass of a proton is 1.6726 × 10-24g, which is about 1836 times that of an electron, so the radius of the <e +, e-> sphere is much larger than that of a hydrogen atom. Since the size of a hydrogen atom is about 1 nm, it is approximately 2 µm (PM0.2 particles) if it is proportional to the reciprocal of the mass ratio with protons. Do you know that this is a quasi-substance? Since electrons are inseparable elementary particles, does this really exist in AS-IS?
真空の誘電率と誘電率って、何が、それを実現してるのか気になり出してきました。
I'm starting to wonder what the permittivity and permittivity of a vacuum make it possible.
電子と陽電子の反応は、不可分なレプトン同士の反応であるはずで、本当に消滅するのであれば、シュレディンガ方程式(ディラック方程式含む)以外の方程式で、波動関数が導き出されないと、おかしいのよね。シュレディンガ方程式を満たすとすると、電子と陽電子が合体した準粒子が出来るはずで、エネルギーもそんなに高くない。 Since Lepton is not divided into finer particles any more, the reaction between electrons and positrons should be a reaction between Leptons, and if it really annihilates, it is an equation other than the Schrodinga equation (including Dirac equation). The wave function should be derived. If the Schrodinger equation is satisfied, a quasiparticle that combines electrons and positrons should be formed, and the energy is not so high.
水素分子と同じように、準粒子2つで分子を構成するかどうかも、気になりますね。要は、2e-と2e+で、1組なのかどうか? As with hydrogen molecules, I'm also wondering if two quasiparticles make up a molecule. In short, is it a pair of 2e- and 2e +?
電子スピンのパウリの排他律を考慮すると、この準粒子の最小エネルギー順位の波動関数は、ψ(↑e+, ↓e+, ↑e-, ↓e-)となるのかな。
Considering Pauli exclusion principle of electron spin, I wonder if the wave function of the minimum energy rank of this quasiparticle is ψ (↑ e +, ↓ e +, ↑ e-, ↓ e-).
TBD
