ALife：チューリング・パターンでクリエイティブ・コーディング

みんな大好き O'reilly さんから、2018/07/28 新刊が出ました。
その名も「作って動かすALife ―実装を通した人工生命モデル理論入門」！

これはクリエイティブ・コーティング界隈の方にとっては待ってました！の内容ではないでしょうか？

早速 Processing でと思いましたが、これコード例が Python なんですよね。
Processing にも Python モードはありますが、Python 2 系だし、numpy 使えないしでどうにも…

そんな中、本書でも紹介されているチューリング・パターンをわかりやすく解説してくれている良いサイトがありましたので、これを Processing の Java で実装してみました。

この記事は全文無料でお読みいただけます。もしお気に召しましたら投げ銭お願いしますね。😉✨

チューリング・パターンとは？

チューリング・パターンとは、ヒョウ柄やゼブラ柄、熱帯魚の模様など自然界の様々な模様を表せると言われるもので、チューリングマシンでお馴染みの天才数学者アラン・チューリングにより発表されたことでその名が付いています。

チューリング・パターンの仕組みはこちらのページの説明がとてもわかりやすかったです。

チューリング波（反応拡散波）を理解したい - Qiita

コードも参考にさせていただきました。

もうひとつ、こちらのコードも参考にさせていただきました。

チューリングパターン　反応拡散系 - ryamadaのコンピュータ・数学メモ

作例

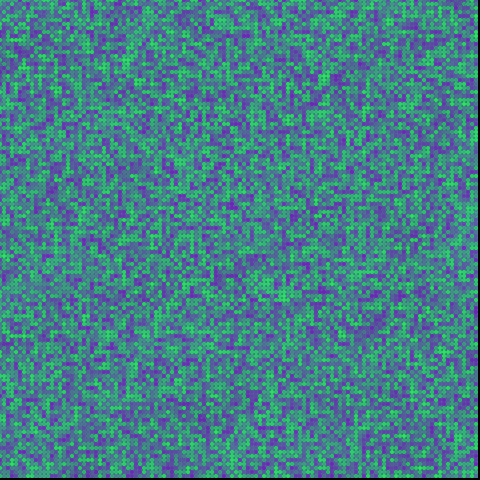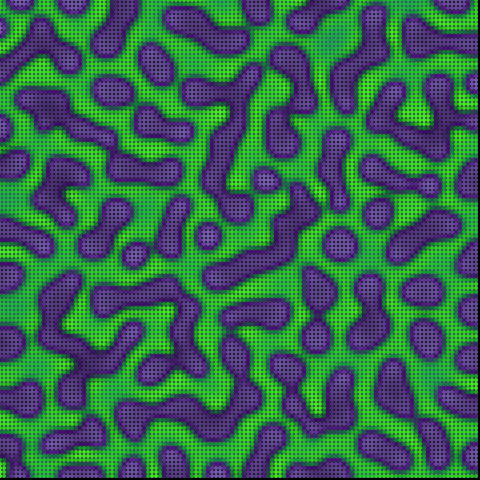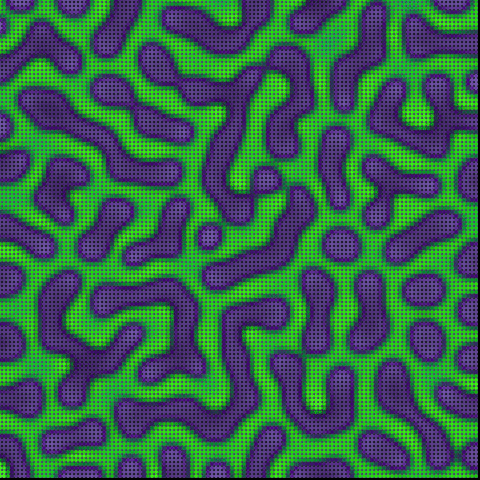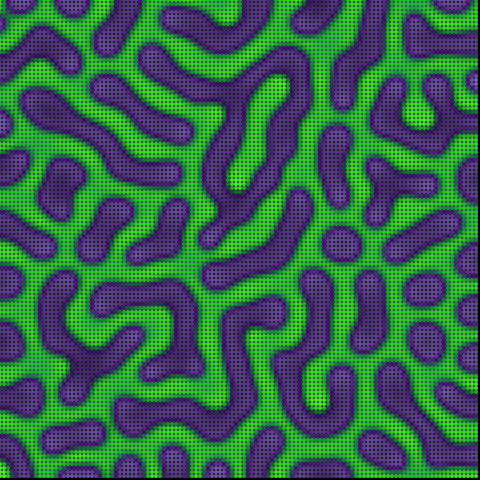
// チューリング・パターン
// @author @deconbatch
// @version 0.2
// Processing 3.2.1
// 2018.07.30

int   lenCellsSide;
int   frameCountMax;
int   calcPerFrame;
float hueBase;
float pSizeX;
float pSizeY;

Cell[][] cells;

/* -------------------- */
void setup() {
  size(600, 600);
  colorMode(HSB, 360.0, 100.0, 100.0, 100.0);
  blendMode(DIFFERENCE);
  smooth();
  noStroke();

  // 動作のためのパラメータ
  lenCellsSide  = 100; // セル群は正方形、一辺の長さ
  frameCountMax = 500; // total frame
  calcPerFrame  = 100; // 1フレーム毎の計算回数
  hueBase       = random(360.0);
  pSizeX        = width / (lenCellsSide * 1.0);
  pSizeY        = height / (lenCellsSide * 1.0);
  cells         = new Cell[lenCellsSide][lenCellsSide];

  // セルの初期化
  for (int y = 0; y < lenCellsSide; y++) {
    for (int x = 0; x < lenCellsSide; x++) {
      cells[y][x] = new Cell(random(1.0), random(1.0));
    }
  }

  // 近隣セルのセット
  for (int y = 0; y < lenCellsSide; y++) {
    for (int x = 0; x < lenCellsSide; x++) {
      cells[y][x].setNeighbor(new Cell[] {
          cells[max(y-1,0)][x],
          cells[min(y+1,lenCellsSide-1)][x],
          cells[y][max(x-1,0)],
          cells[y][min(x+1,lenCellsSide-1)]
        });
    }
  }
}

void draw() {
  background(0.0, 0.0, 0.0, 100.0);

  // チューリング・パターン算出
  for (int i = 0; i < calcPerFrame; i++) {
    for (int y = 0; y < lenCellsSide; y++) {
      for (int x = 0; x < lenCellsSide; x++) {
        cells[y][x].delta();
      }
    }
    for (int y = 0; y < lenCellsSide; y++) {
      for (int x = 0; x < lenCellsSide; x++) {
        cells[y][x].sum();
      }
    }
  }

  // 結果を描画
  for (int y = 0; y < lenCellsSide; y++) {
    for (int x = 0; x < lenCellsSide; x++) {
      fill(
           hueBase,
           40.0,
           cells[y][x].getStandardU(),
           100.0
           );
      rect(x * pSizeX, y * pSizeY, pSizeX, pSizeY);
      fill(
           (hueBase + 120.0) % 360.0,
           40.0,
           cells[y][x].getStandardV(),
           100.0
           );
      rect(x * pSizeX, y * pSizeY, pSizeX, pSizeY);
    }
  }

  textSize(20);
  fill(0, 0, 100, 100);
  text(frameCount, width-80, height-30);

  if (frameCount >= frameCountMax) {
    exit();
  }
  
}

/* 各セル毎に計算値を保持するクラス -------------------- */
public class Cell {

  // パターンを形作るパラメータ
  private float paramA   = 0.00028;
  private float paramB   = 0.005;
  private float paramTau = 0.1;
  private float paramK   = -0.005;
  private float dt       = 0.001; // time step per frame
  private float dx       = 0.02;  // space step

  private float valueU;
  private float valueV;
  private float deltaU;
  private float deltaV;

  private Cell[] neighbor;

  Cell (float initU, float initV) {
    valueU = initU;
    valueV = initV;
    resetDelta();
  }

  private void resetDelta() {
    deltaU = 0.0;
    deltaV = 0.0;
  }

  public void setNeighbor(Cell[] pNeighbor) {
    neighbor = new Cell[pNeighbor.length];
    for (int i = 0; i < pNeighbor.length; ++i) {
      neighbor[i] = pNeighbor[i];
    }
  }

  public float getStandardU() {
    return map(valueU, -1.0, 1.0, 0.0, 100.0);
  }

  public float getStandardV() {
    return map(valueV, -1.0, 1.0, 0.0, 100.0);
  }
  
  public void delta() {
    float sumU = 0.0;
    float sumV = 0.0;
    for (int i = 0; i < neighbor.length; ++i) {
      sumU += neighbor[i].valueU;
      sumV += neighbor[i].valueV;
    }
    deltaU = (sumU - valueU * neighbor.length) / (dx*dx);
    deltaV = (sumV - valueV * neighbor.length) / (dx*dx);
  }

  public void sum() {
    float postU = valueU + dt * (paramA * deltaU + valueU - pow(valueU, 3) - valueV + paramK);
    float postV = valueV + dt * (paramB * deltaV + valueU - valueV) / paramTau;
    valueU = constrain(postU, -1.0, 1.0);
    valueV = constrain(postV, -1.0, 1.0);
    resetDelta();
  }
  
}



/*
Copyright (C) 2018- deconbatch

This program is free software: you can redistribute it and/or modify
it under the terms of the GNU General Public License as published by
the Free Software Foundation; either version 3 of the License, or
(at your option) any later version.

This program is distributed in the hope that it will be useful,
but WITHOUT ANY WARRANTY; without even the implied warranty of
MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE.  See the
GNU General Public License for more details.

You should have received a copy of the GNU General Public License
along with this program.  If not, see <http://www.gnu.org/licenses/>
*/

ライセンスは GPLv3 にさせていただきました。
ご自由にお使いください。

初期配置によってはキモくない

上の例はセルの初期配置をランダムにしたものですが、これを幾何学的な配置にすると全然キモくなくなります。

// セルの初期化
for (int y = 0; y < lenCellsSide; y++) {
  for (int x = 0; x < lenCellsSide; x++) {
    // cells[y][x] = new Cell(random(1.0), random(1.0));
    cells[y][x] = new Cell((x * y) % 2, (x + y) % 2);
  }
}

生物っぽさも無いですね。

このように初期配置を変えても出来上がる模様は変わりますし、初期パラメータを変えて描画してみたり、アニメーションの途中でパラメータの値を変化させたり、描画の仕方を変えてみたり、いろいろと改造のしがいがありそうです。

天才チューリング

今回、数式はわかっていても、それをコードに起こすのに私は四苦八苦しました。
コンピュータも無かった時代、この数式でこんな模様が描けると証明できたなんてすご過ぎます。

チューリングの論文発表は 1952年、チューリングとしては数式を用いて生物の謎を解くことを考えていたそうですが、長らく生物界では研究されてきませんでした。
しかし 1995年になって、ある魚の模様が実際にチューリング・パターンであることが確認されたのだそうです。

やはり、天才チューリング。恐るべし。

最初に紹介した O'reilly さんの「作って動かすALife ―実装を通した人工生命モデル理論入門」にはチューリング・パターンの他にもまだまだ面白いモデルが沢山掲載されています。
ぜひ、お近くの書店でお求めください！（誰目線？）

お近くに大きな書店の無い方は Amazon でも取扱いありますよ。

Amazon で購入 「O'reilly Japan 作って動かすALife ―実装を通した人工生命モデル理論入門」

そして、面白いもの作って私にも見せてください。
あなたの作ったものを、私は見たい！

更新履歴
18/07/28 初版
18/07/30 コードをリファクタリング

ここでこの記事はおしまいです。もしこの記事がお気に召しましたら投げ銭お願いします。😉✨