機械学習：有益な特徴量を選ぶ　正則化

2023年7月13日 06:45

機械学習モデルが、trainデータに対して複雑すぎると、testデータよりもtrainデータで高い性能を出す過適合（over fitting）が起こりやすいと言われています。　これを防ぐには、

より多くのtrainデータを集める
正則化を通じて複雑さにペナルティを課す
パラメータを少なくして学習モデルをシンプルにする
データの次元数（特徴量の種類を減らす）

の方法があります。
　ここでは、二番目の正規化を通じて複雑さにペナルティを課す方法を扱います。
　

L1／L2正則化

各特徴量$${X^i}$$にかける重みを$${w_i}$$とし、特徴量がm種類存在するとすれば、この重みを使い、L2、L1正則化は以下の其々の式を、正則化の強弱を示す係数$${C}$$と共に、損失関数（cost function)に加えるのが正則化の定義です。

$${\textrm{the cost function}_{norm}=C \times \textrm{the original cost funtion} + ( \| W \|_1 \textrm{ or } \frac{1}{2}\| W \|^2_2) }$$

L2正則化：$${\| W \|^2_2=\displaystyle{\sum^{m}_{j=1}w^2_j}}$$
L1正則化：$${\| W \|_1=\displaystyle{\sum^{m}_{j=1}|w_j| } }$$

損失関数を最小にするように学習していくので、L1正則化を強めれば、ほとんどの特徴量への重みはゼロになります。このL1正則化に効果があるのは、学習に無関係な特徴量の個数が多い（高次元）のデータセットに対してで、特に無関係な次元数がtrainデータよりも多い場合となります。
　L1正則化は、sklearn.linear_modelの LogisticRegressionで、サポートされています。

from sklearn.linear_model import LogisticRegression

lr = LogisticRegression(penalty='l1', C=1.0, solver='liblinear', multi_class='ovr')

lr.fit(X_train_std, y_train)
print('Training accuracy:', lr.score(X_train_std, y_train))
print('Test accuracy:', lr.score(X_test_std, y_test))

　$${C}$$は正則化の強さを示し、$${C=1.0}$$がデフォルトの値で、$${1}$$より小さくとれば正則化は強まり、大きくすれば正則化が弱くなります。ただし、solverがlbfgsの場合、L1はサポートされていません。
　係数$${C}$$は、ユーザ自身が設定する値で、デフォルトが一般的に通用する値かどうかはモデルにより、一般には、正則化パラメータを変えて学習を繰り返し、適切な値を探すことになります。

weights, params = [], []
for c in np.arange(-4., 6.):
    lr = LogisticRegression(penalty='l1', C=10.**c, solver='liblinear', 
                            multi_class='ovr', random_state=0)
    lr.fit(X_train_std, y_train)
    weights.append(lr.coef_[1])
    params.append(10**c)

weights = np.array(weights)

forループで、Cを$${10^{-4}}$$から$${10^{-5}}$$まで変えて、L1正則化がこの強さが入った結果のweightを配列に加え入れています。
　この最初のCが$${10^{-4}}$$の時のweightは、

正則化が強く、全てゼロです。
では、最後のCが$${10^{-5}}$$の時のweightは、

ここで何が起こっているかというと、Cが小さく正則化が強すぎると、全ての特徴量は学習モデルによって重要ではないと判断され、逆にCが大きくて正則化が弱いと、今度は全ての特徴量が重要だと判断されて全てモデルの考慮に入っているのです。
　この結果をグラフにするともっとわかりやすく、

import matplotlib.pyplot as plt

fig = plt.figure()
ax = plt.subplot(111)
    
colors = ['blue', 'green', 'red', 'cyan', 
          'magenta', 'yellow', 'black', 
          'pink', 'lightgreen', 'lightblue', 
          'gray', 'indigo', 'orange']
for column, color in zip(range(weights.shape[1]), colors):
    plt.plot(params, weights[:, column],
             label=df_wine.columns[column + 1],
             color=color)
plt.axhline(0, color='black', linestyle='--', linewidth=3)
plt.xlim([10**(-5), 10**5])
plt.ylabel('weight coefficient')
plt.xlabel('C')
plt.xscale('log')
plt.legend(loc='upper left')
ax.legend(loc='upper center', 
          bbox_to_anchor=(1.38, 1.03),
          ncol=1, fancybox=True)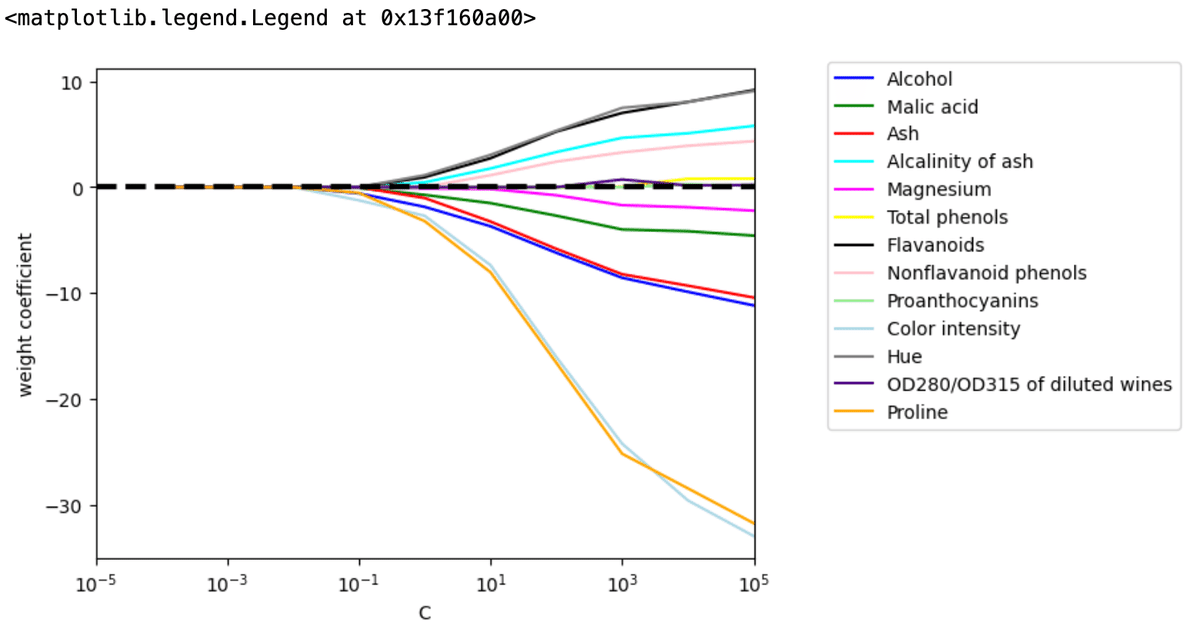

このワインのクラス分け学習には、L1正則化パラメータの適切な範囲は$${10^{-1}\ge C \le 10^{1}}$$で、広くしたといえども、上限下限共に$${O(\pm2)}$$と設定した方が良いことがわかります。

　Logistic Regressionの正則化のデフォルトはL2正則化です。L1に比べ、マイルドに重みを小さくするのがL2正則化だからです。
　L２正則化でsolverをlbfgsにして、上と同じ$${C}$$の範囲で重みの変化を見ると、

weights, params = [], []
for c in np.arange(-4., 6.):
    lr = LogisticRegression(C=10.**c, solver='lbfgs', 
                            multi_class='ovr', random_state=0)
    lr.fit(X_train_std, y_train)
    weights.append(lr.coef_[1])
    params.append(10.**c)

weights = np.array(weights)

　となります。
　なぜL2の方がマイルドにweightを小さくできるかは、数学的直感で言えば、足し上げが二乗で行われているからです。L1、L2の名前は、ノルムの取り方の、マンハッタン距離のL1、ユークリッド距離のL2から来ています。

機械学習：有益な特徴量を選ぶ 正則化

L1／L2正則化

いいなと思ったら応援しよう！

機械学習：有益な特徴量を選ぶ　正則化