ファイナンス機械学習:ファイナンスにおける交差検証法 練習問題 シャッフル 分数差分とトリプルバリア適用後のランダムフォレスト
ファイナンスで扱うデータは時系列であって、シャッフルをすると、そのデータに含まれている過去の情報が薄まる可能性がある。
k-分割交差検証を行う前にデータセットをシャッフルした場合で、テストデータとテストデータのインデックスを調べてみる。
X0=X[:10]
y0=y = Xy['bin'][:10].to_frame
kf = KFold(n_splits=5)
for train_index, test_index in kf.split(X0):
print("Without Shuffle TRAIN:", train_index, "TEST:", test_index)
kf1 = KFold(n_splits=5, shuffle=True, random_state=0)
for train_index, test_index in kf1.split(X0):
print("With Shuffle TRAIN:", train_index, "TEST:", test_index)簡単化のため、テストデータを10セットしている。これを5分割したとすると、シャッフルありと無しのインデックスは以下のようになった。

訓練データでは、時系列の分断箇所が増えており、かつテストデータで、インデックスが不連続になっている。これにより、バリアンスが減り、バイアスが減っているので、一般的に学習器のパフォーマンスは上がる。しかしながら、時系列データ解析を扱う時系列モデルにおいて、結果に意味があるかどうかは疑わしい。
E-mini S&P500の先物ティックデータで、ドルバーを取り、これにトリプルバリアを適用したラベルを使って、ランダムフォレスト分類器の10分割交差検証をシャッフル有無で行う。
from datetime import datetime
import Labels as labels
import Bars as bars
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import confusion_matrix
from sklearn.metrics import roc_curve,auc
from sklearn.metrics import classification_report
SP_data = pd.read_csv('SP.csv')
SP_data = SP_data[SP_data['volume'] > 0]
SP_data['datetime'] = SP_data['date'] + "/" + SP_data['time']
SP_data['datetime'] = SP_data['datetime'].apply(lambda dt: datetime.strptime(dt, '%m/%d/%Y/%H:%M:%S.%f'))
SP_data=SP_data[SP_data['datetime'] >= datetime(2009, 1, 1)]
SP_data.index=SP_data['datetime']
SP_data.drop(['date','time'],axis=1, inplace=True)
SP_data.drop(['datetime'],axis=1, inplace=True)
SP_data.volume=SP_data.groupby(SP_data.index).volume.sum()
SP_data = SP_data[~SP_data.index.duplicated(keep='first')]
dv=200_000
Dbar=bars.getDollarBars(SP_data,dv)ここで、ドルバーの分数差分を固定ウィンドウ法で取り、非定常性を取り除き、定常時系列とした。
dc,outADF=fdiff.plotMinFFD(Dbar["Close"].to_frame(),True,1e-5,dmin=0.01,dmax=0.75,dnum=75)
dh,outADF=fdiff.plotMinFFD(Dbar["High"].to_frame(),True,1e-5,dmin=0.01,dmax=0.75,dnum=75)
dl,outADF=fdiff.plotMinFFD(Dbar["Low"].to_frame(),True,1e-5,dmin=0.01,dmax=0.75,dnum=75)
DDF_Close=fdiff.fracDiff_FFD(Dbar['Close'].to_frame(), d=dc, thres=1e-5).dropna()
print('Close')
fdiff.printADF(DDF_Close)
DDF_High=fdiff.fracDiff_FFD(Dbar['High'].to_frame(), d=dh, thres=1e-5).dropna()
print('High')
fdiff.printADF(DDF_High)
DDF_Low=fdiff.fracDiff_FFD(Dbar['Low'].to_frame(), d=dl, thres=1e-5).dropna()
print('Low')
fdiff.printADF(DDF_Low)
DDF=pd.DataFrame({
'Close':DDF_Close.Close,
'High':DDF_High.High,
'Low':DDF_Low.Low
}).dropna()
DDF
これから、ボリンジャーバンドのゴールドクロスを買い、デッドクロスで売りの空売りなしで、サイドを決め、トリプルバリアを適用し、メタラベルをつけた。
span=20
DDFBB=bars.getBBand(DDF,span,1.0)
DCross, GCross = labels.getDCrossBB(DDFBB), labels.getGCrossBB(DDFBB)
buy = pd.Series(1, index=GCross.index)
sell = pd.Series(-1, index=DCross.index)
side = pd.concat([sell,buy]).sort_index()
minRet = .005
ptsl=[0,2]
span0=20
price=DDF['Close']
daily_vol=labels.getDailyVol(price,span0)
h=daily_vol.mean()
ddf_rtn = price.pct_change().dropna()
events=bars.getTEvents(ddf_rtn.loc[daily_vol.index[0]:], h) #CUSUM
t1 = labels.addVerticalBarrier(price, events, numDays=1)
BBPevents=labels.getEventsML(price,events,ptsl,daily_vol,minRet,t1=t1,side=side)
BBPevents=BBPevents.dropna()
BBlabels=labels.getBinsTUML(BBPevents,price,t1)
BBlabels.bin.value_counts()

ランダムフォレストに与えるデータセットを以下のように作成する。
Xy = pd.DataFrame({'vol': daily_vol,
'side': side,
'corr': labels.getDailyCorr(price,span0),
'BBU':DDFBB['BB_u'],
'BBD':DDFBB['BB_d'],
'TP':DDFBB['TP'],
'bin':BBlabels['bin'] }).dropna()
Xy = Xy[~Xy.index.duplicated(keep='first')]
Xy
トリプルバリアで使ったt1から、独自性を計算する。この値は、ランダムフォレストのmax_samplesに渡される。
import Weights as wg
CoEvents=wg.getNumCoEvents(Xy.index, t1=t1, period=Xy.index)
avgUniq=wg.getSampleTW(t1=t1,numCoEvents=CoEvents,period=Xy.index)
avgU=avgUniq.mean()
avgU
ランダムフォレストを定義する。
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import StratifiedKFold, KFold
X = Xy.drop('bin',axis=1)
y = Xy['bin'].to_frame
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, shuffle=False)
rf = RandomForestClassifier(n_estimators = 1000,
criterion = "entropy",
max_samples=avgU,
bootstrap=True,
n_jobs=1,
random_state=1,
class_weight="balanced_subsample",
oob_score=False) スニペット7.4のcvScoreにROC曲線をプロットするように拡張する。
def plotCVROC(clf,X,y,sample_weight=None,scoring='neg_log_loss',
t1=None,cv=None,cvGen=None,pctEmbargo=None):
if scoring not in ['neg_log_loss','accuracy']:
raise Exception('wrong scoring method.')
from sklearn.metrics import log_loss,accuracy_score
from sklearn.metrics import RocCurveDisplay, auc
idx = pd.IndexSlice
if cvGen is None:
cvGen=PurgedKFold(n_splits=cv,t1=t1,pctEmbargo=pctEmbargo) # purged
score=[]
tprs = []
aucs = []
mean_fpr = np.linspace(0, 1, 100)
fig, ax = plt.subplots(figsize=(12, 8))
mean_fpr = np.linspace(0, 1, 100)
for i, (train, test) in enumerate(cvGen.split(X=X)):
if sample_weight is not None:
fit=clf.fit(X=X.iloc[idx[train],:],y=y.iloc[idx[train].values.ravel()],
sample_weight=sample_weight.iloc[idx[train]].values)
if scoring=='neg_log_loss':
prob=fit.predict_proba(X.iloc[idx[test],:])
score_=-log_loss(y.iloc[idx[test]], prob,
sample_weight=sample_weight.iloc[idx[test]].values,
labels=clf.classes_)
else:
pred=fit.predict(X.iloc[idx[test],:])
score_=accuracy_score(y.iloc[idx[test]],pred,
sample_weight=sample_weight.iloc[idx[test]].values)
viz = RocCurveDisplay.from_estimator(
clf,
X.iloc[idx[test],:],
y.iloc[idx[test]],
sample_weight=sample_weight.iloc[idx[test]].value,
name=f"ROC fold {i}",
alpha=0.3,
lw=1,
ax=ax)
else:
fit=clf.fit(X=X.iloc[idx[train],:],y=y.iloc[idx[train]].values.ravel())
if scoring=='neg_log_loss':
prob=fit.predict_proba(X.iloc[idx[test],:])
score_=-log_loss(y.iloc[idx[test]], prob,
labels=clf.classes_)
else:
pred=fit.predict(X.iloc[idx[test],:])
score_=accuracy_score(y.iloc[idx[test]],pred)
viz = RocCurveDisplay.from_estimator(
clf,
X.iloc[idx[test],:],
y.iloc[idx[test]],
sample_weight=None,
name=f"ROC fold {i}",
alpha=0.3,
lw=1,
ax=ax)
score.append(score_)
interp_tpr = np.interp(mean_fpr, viz.fpr, viz.tpr)
interp_tpr[0] = 0.0
tprs.append(interp_tpr)
aucs.append(viz.roc_auc)
ax.plot([0, 1], [0, 1], linestyle="--", lw=2, color="r", label="Chance", alpha=0.8)
mean_tpr = np.mean(tprs, axis=0)
mean_tpr[-1] = 1.0
mean_auc = auc(mean_fpr, mean_tpr)
std_auc = np.std(aucs)
ax.plot(mean_fpr, mean_tpr, color="b", label=r"Mean ROC (AUC = %0.2f $\pm$ %0.2f)" % (mean_auc, std_auc),
lw=2, alpha=0.8)
std_tpr = np.std(tprs, axis=0)
tprs_upper = np.minimum(mean_tpr + std_tpr, 1)
tprs_lower = np.maximum(mean_tpr - std_tpr, 0)
ax.fill_between(mean_fpr, tprs_lower, tprs_upper, color="grey", alpha=0.2, label=r"$\pm$ 1 std. dev.")
ax.set(xlim=[-0.05, 1.05], ylim=[-0.05, 1.05], title="Receiver operating characteristic")
ax.legend(loc="lower right")
plt.show()
print('RFclf Mean CV score: {0:.6f}\nCV Variance: {1:.6f}'.format(np.array(score).mean(), np.array(score).var()))
return np.array(score)これを使い、シャッフル無しと有りとでk-fold交差検証法を比較する。
cv = KFold(n_splits=10, shuffle=False)
plotCVROC(clf=rf, cvGen=cv, X=X, y=y)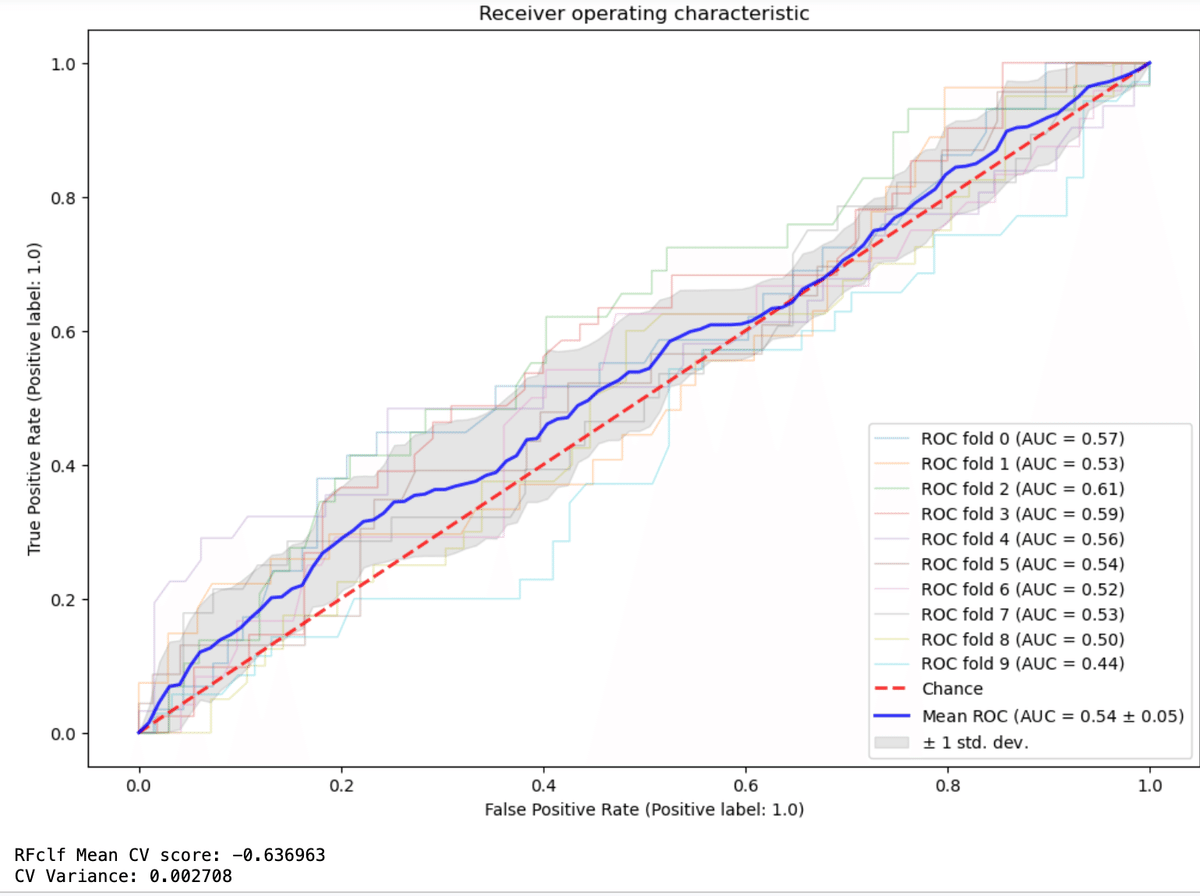
cv1 = KFold(n_splits=10, shuffle=True)
plotCVROC(clf=rf, cvGen=cv1, X=X, y=y)
同じランダムフォレストに、1%のエンバーゴを適用し、パージされた10分割交差検証法のパフォーマンスを測定する。
cvGenEmb=PurgedKFold(n_splits=5, t1=t1[X.index], pctEmbargo=0.01)
plotCVROC(clf=rf, cvGen=cvGenEmb, X=X, y=y)
シャッフル無し、エンバーゴとパージングを入れたランダムフォレストの交差検証のパフォーマンスは、加工なしの交差検証よりもパフォーマンスは低くなる。これは、情報のリーケージがなくなり、機械学習のモデルを正しく評価しているからである。
