ファイナンス機械学習：ベットサイズの決定　練習問題　ロングベット、ショートベットの数からベットサイズを求める

Dean4rmEdinburgh

前記事で作成したEventsを用いて、同時刻でアクティブなロングベット、ショートベットの最大数$${\bar{c_l},\bar{c_s}}$$を求める。

def getCurrentBets(Events):
    Long=pd.Series(dtype='int64',index=Events.index)
    Short=pd.Series(dtype='int64',index=Events.index)
    tPnts = set(Events['t1'].dropna().values)
    tPnts = tPnts.union(Events.index.values)
    tPnts = sorted(list(tPnts));
    out = pd.Series(dtype='float64')
    for loc in tPnts:
        df0 = (Events.index.values <= loc) & ((loc < Events['t1']) | pd.isnull(Events['t1']))
        act = Events[df0].index
        if len(act) > 0:
            Long[loc]=sum(Events.loc[act, 'side']>0)
            Short[loc]=sum(Events.loc[act, 'side']<0)
        else:
            Long[loc]=0
            Short[loc]=0
    return Long, Short 

Events['Long'],Events['Short']=getCurrentBets(Events)
Events.describe()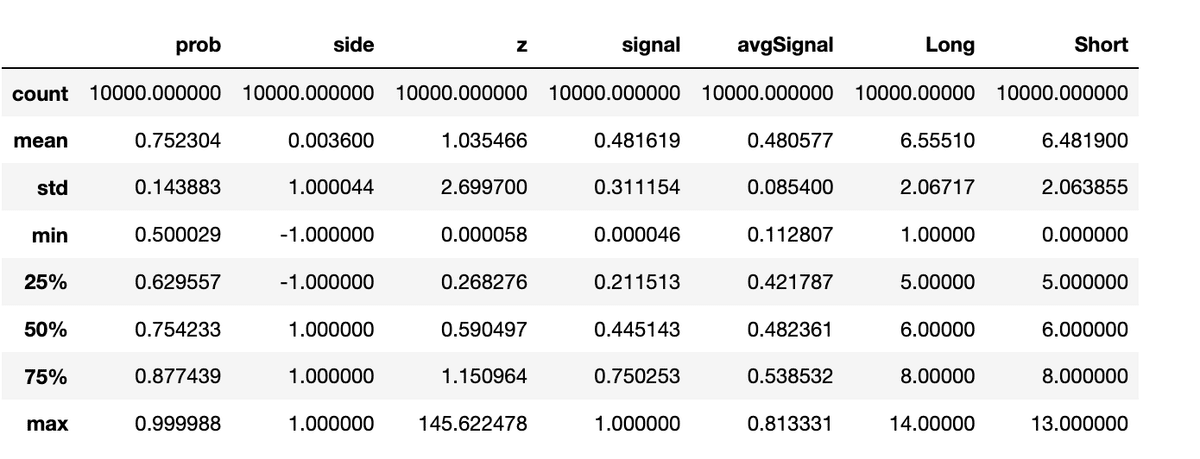
同時発生ロング/ショートベット数

これを用いて、時刻tのベットサイズ、
$${m_t=\displaystyle{\frac{c_{t,l}}{\bar{c_l}}-\frac{c_{t,s}}{\bar{c_s}} }}$$
を計算する。

maxCl=Events['Long'].max()
maxCs=Events['Short'].max()
Events['betSizeClCs']=Events['Long']/maxCl-Events['Short']/maxCs
Events.describe()
同時刻のロングべット、ショートベットからのベットサイズ　betSizeClCs

同じEventsを使い、ロングベットとショートベットの差を計算し、ガウス混合分布を当てはめる。

Events['ct']=Events['Long']-Events['Short']

from sklearn.mixture import GaussianMixture

gmm = GaussianMixture(n_components=2).fit(np.array(Events.ct).reshape(-1, 1))

fig, ax = plt.subplots(figsize=(12, 8))
x = np.linspace(-15, 15, 1000).reshape(-1, 1)
logprob = gmm.score_samples(x)
pdf = np.exp(logprob)

ax.plot(x, norm.pdf(x,loc=gmm.means_[0,-1],scale=gmm.covariances_[0]), label='Gauss 1' )
ax.plot(x, norm.pdf(x,loc=gmm.means_[1,-1],scale=gmm.covariances_[1]), label='Gauss 2' )
ax.plot(x, pdf, color='red', label='Gaussian Mixture')

ax.hist(Events['ct'], density=True, label='Histogram of c series')
ax.legend(loc='best')
plt.show()
ロングベットとショートベットの差とガウス混合分布

　求めたガウス混合分布のCDF、$${F[.]}$$を使い、ベットサイズ、
$${\displaystyle{m_t =\begin{cases}\frac{F[c_t]-F[0]}{1-F[0]}& (c_t \geq 0)\\ \frac{F[c_t]-F[0]}{F[0]}& (c_t \lt 0)\end{cases}}}$$
を計算する。

x0 = np.linspace(-15, 0, 1000).reshape(-1, 1)
logprob0 = gmm.score_samples(x0)
cdf0 = np.exp(logprob0).sum()*15/1000
cdf1 = 1 - cdf0

for idx in Events.index:
    ct=Events.loc[idx,'ct']
    xt=np.linspace(-15,ct,1000).reshape(-1, 1)
    logprobt = gmm.score_samples(xt)
    cdft = np.exp(logprobt).sum()*(15+ct)/1000
    if ct >= 0 : 
        mt=(cdft - cdf0)/cdf1
    else: 
        mt=(cdft - cdf0)/cdf0
    Events.loc[idx,'betSize cdf']=mt
    
Events[['betSizeClCs','betSize cdf']].describe()

いいなと思ったら応援しよう！