ファイナンス機械学習 Financial Data Structures 練習問題 標準バー
E-mini S&P 500 先物tickデータに対し、tick bar, volume bar, dollar barを作成する。
E-mini S&P 500 先物tickデータを以下のサイトからダウンロードし、2009年以降の10年分のデータを読み込む。
import pandas as pd
import numpy as np
from datetime import datetime,timedelta, date
from tqdm.notebook import tqdm
from plotly.subplots import make_subplots
import matplotlib.pyplot as plt
%matplotlib inlineSP_data = pd.read_csv('SP.csv')
SP_data = SP_data[SP_data['volume'] > 0]
SP_data['datetime'] = SP_data['date'] + "/" + SP_data['time']
SP_data['datetime'] = SP_data['datetime'].apply(lambda dt: datetime.strptime(dt, '%m/%d/%Y/%H:%M:%S.%f'))
SP_data=SP_data[SP_data['datetime'] >= datetime(2009, 1, 1)]
SP_data.index=SP_data['datetime']
SP_data.drop(['date','time'],axis=1, inplace=True)
SP_data.drop(['datetime'],axis=1, inplace=True)
SP_data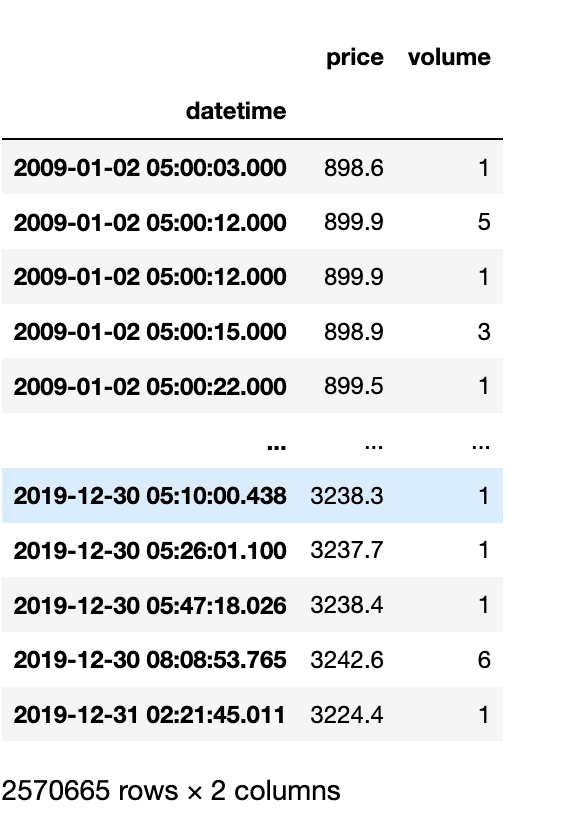
Tick Bar
def bars_df(bars):
return pd.DataFrame(data=bars[:,1:], index=bars[:,0],
columns=['Open','High','Low','Close','Volume'])
def getTickBars(data, freq):
prices=data['price'].to_numpy()
datetimes=data.index.to_numpy()
vols=data['volume'].to_numpy()
bars = np.zeros(shape=(len(range(freq, len(prices), freq)), 6), dtype=object)
ind = 0
for i in range(freq, len(prices), freq):
bars[ind][0] = datetimes[i - 1] # time
bars[ind][1] = prices[i - freq] # open
bars[ind][2] = np.max(prices[i - freq: i]) # high
bars[ind][3] = np.min(prices[i - freq: i]) # low
bars[ind][4] = prices[i - 1] # close
bars[ind][5] = np.sum(vols[i - freq: i]) # volume
ind += 1
return bars_df(bars)Volume Bar
def getVolumeBars(data,bar_vol):
prices=data['price'].to_numpy()
datetimes=data.index.to_numpy()
vols=data['volume'].to_numpy()
bars = np.zeros(shape=(len(prices), 6), dtype=object)
ind = 0
last_tick = 0
cur_volume = 0
for i in range(len(prices)):
cur_volume += vols[i]
if cur_volume >= bar_vol:
bars[ind][0] = datetimes[i - 1] # time
bars[ind][1] = prices[last_tick] # open
bars[ind][2] = np.max(prices[last_tick: i + 1]) # high
bars[ind][3] = np.min(prices[last_tick: i + 1]) # low
bars[ind][4] = prices[i] # close
bars[ind][5] = np.sum(vols[last_tick: i + 1]) # volume
cur_volume = 0
last_tick = i + 1
ind += 1
return bars_df(bars[:ind])Dollar Bar
def getDollarBars(data,bar_dol):
prices=data['price'].to_numpy()
datetimes=data.index.to_numpy()
vols=data['volume'].to_numpy()
bars = np.zeros(shape=(len(prices), 6), dtype=object)
ind = 0
last_tick = 0
cur_sum = 0
for i in range(len(prices)):
cur_sum += vols[i] * prices[i]
if cur_sum >= bar_dol:
bars[ind][0] = datetimes[i - 1] # time
bars[ind][1] = prices[last_tick] # open
bars[ind][2] = np.max(prices[last_tick: i + 1]) # high
bars[ind][3] = np.min(prices[last_tick: i + 1]) # low
bars[ind][4] = prices[i] # close
bars[ind][5] = np.sum(vols[last_tick: i + 1]) # volume
cur_sum = 0
last_tick = i + 1
ind += 1
return bars_df(bars[:ind])Fix Time Bar
def getTBars(data,freq):
volume=data.groupby(pd.Grouper(level=0, freq=freq))['volume'].sum()
high=data.groupby(pd.Grouper(level=0, freq=freq))['price'].max()
low=data.groupby(pd.Grouper(level=0, freq=freq))['price'].min()
open_price=data.groupby(pd.Grouper(level=0, freq=freq))['price'].first()
close_price=data.groupby(pd.Grouper(level=0, freq=freq))['price'].last()
return pd.concat([open_price, high,low, close_price, volume],
keys=['open','high','low','close','volume'],
axis=1)サンプリングの安定性
固定時間バー以外、Tick Bar, Dollar Bar, Volume Barは、閾値を上げるほど、サンプリングはより安定する。
def getNumBarsEWMA(df_bar,freq,span=5):
df = df_bar['Close'].groupby(pd.Grouper(level=0, freq=freq)).count()
return df.ewm(span=span).mean()fig = plt.figure(figsize=(14, 8))
for dv in (500000,1000000,5000000,10000000):
ddf=getDollarBars(SP_data,dv)
ewm=getNumBarsEWMA(ddf,"D",365)
plt.plot(ewm[365:],ls='-', label=f'dv={dv}')
plt.xlabel('Day')
plt.ylabel('EWMA')
plt.title('EWMA(Day number of Dollar Bar)')
plt.legend()
plt.show()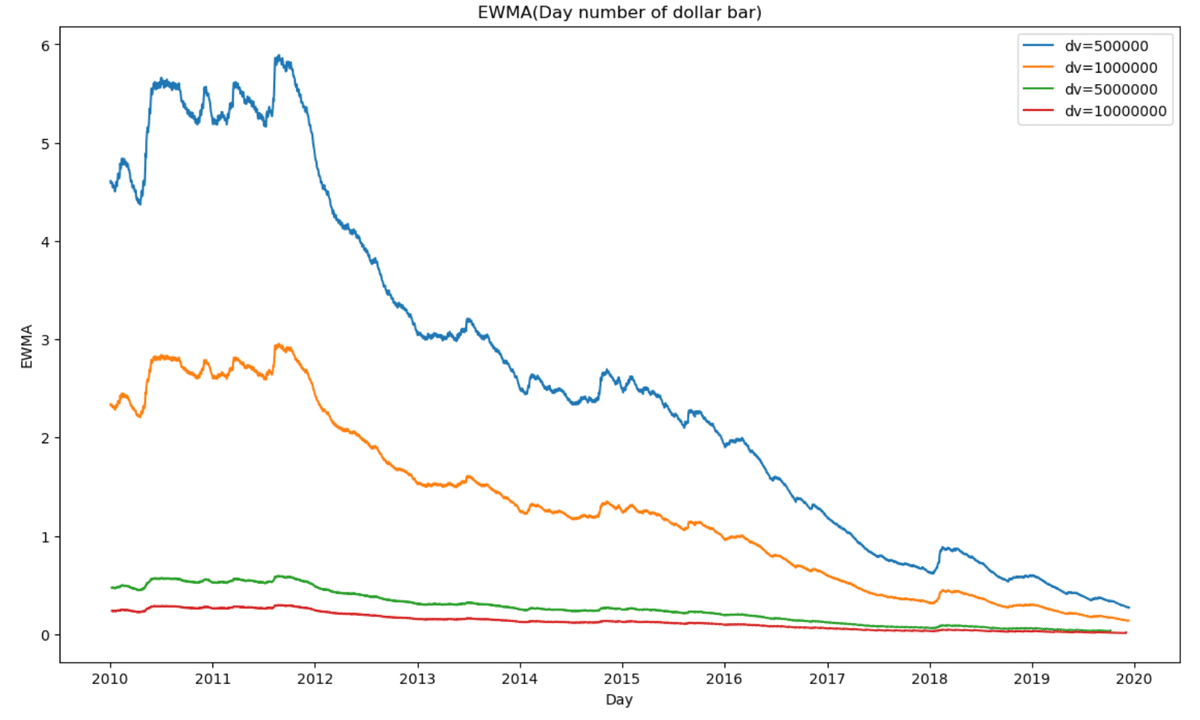
Tick Bar, Dollar Bar, Volume Barの週次のバー数を数え、EWMAをとり、分散と相関を計算する。
n_ticks = SP_data.shape[0]
v_tick=SP_data['volume'].sum()/n_ticks
d_tick=(SP_data['volume']*SP_data['price']).sum()/n_ticks
tv=3000
vv=tv*v_tick
dv=tv*d_tick
print(tv,vv,dv)
tdf=getTickBars(SP_data,tv)
ddf=getDollarBars(SP_data,dv)
vdf=getVolumeBars(SP_data,vv)
fig = plt.figure(figsize=(14, 8))
span=48
for bars, name in [(tdf, 'Tick Bars'), (vdf, 'Volume Bars'), (ddf, 'Dollar Bars')]:
ewm=getNumBarsEWMA(bars,"W",span)
print(f'{name} std: {np.std(ewm[span:])} autocorr: {ewm[span:].autocorr()}')
plt.plot(ewm[span:],ls='-', label=f'{name}')
plt.xlabel('Date')
plt.ylabel('EWMA')
plt.title('EWMA(Week number of bars)')
plt.legend()
plt.show()
ドルバーが最も安定していると言える。
次に、其々のリターン系列をとり、相関を計算する。
tdf_r_corr = tdf['Close'].pct_change().dropna().autocorr()
vdf_r_corr = vdf['Close'].pct_change().dropna().autocorr()
ddf_r_corr = ddf['Close'].pct_change().dropna().autocorr()
print('Tick Bar:',tdf_r_corr)
print('Volume Bar:', vdf_r_corr)
print('Dollar Bar:',ddf_r_corr)
月次のリターンを計算し、その分散と分散の分散を調べる。
tdf_mr = tdf['Close'].pct_change().dropna().resample("M").var().dropna()
vdf_mr = vdf['Close'].pct_change().dropna().resample("M").var().dropna()
ddf_mr = ddf['Close'].pct_change().dropna().resample("M").var().dropna()
print('Tick Bar:',tdf_mr.var())
print('Volume Bar:', vdf_mr.var())
print('Dollar Bar:',ddf_mr.var())
各バーのリターンのジャックベラ検定の検定統計量
from scipy import stats
ddf_jb = stats.jarque_bera(ddf['Close'].pct_change().dropna()).statistic
vdf_jb = stats.jarque_bera(vdf['Close'].pct_change().dropna()).statistic
tdf_jb = stats.jarque_bera(tdf['Close'].pct_change().dropna()).statistic
print('Tick Bar:',tdf_jb)
print('Volume Bar:', vdf_jb)
print('Dollar Bar:',ddf_jb)
検定統計量が最小なのは、ドルバー。
この記事が気に入ったらサポートをしてみませんか?
