機械学習：階層的クラスタリング　凝縮型階層的アルゴリズム

階層的クラスタリングは、分割法とは違い、クラスタの数を指定する必要はなく、樹形図でクラスタの階層を可視化できるという利点がある。
　データポイントの全てを含む一つのクラスタから、全てのクラスタにデータポイントが一つだけ含まれるまで分割を繰り返すトップダウン型と、個々のデータポイントをクラスタとみなして、最近のクラスタを結合させ、クラスタが一つになるまで結合させていくボトムアップ方の二つがある。

ボトムアップ法

　最近接している二つのクラスタを結合するアルゴリズムには、ペアにした二つのクラスタ内の最も類似度の高い（距離測度が小さい）データポイントの距離を比較し、この距離が最小であるクラスタ同士を結合する単連結法と、逆に類似度の低い（距離測度が大きい）データポイントの距離が最小になるクラスタを結合してく完全連結法がある。
　完全連結法の手順は以下の通りとなる。

1. 全てのデータポイントの距離行列（対称行列）を作成する。

2. 最も距離が大きいデータポイント同士のクラスタを最小にするようにクラスタを結合させる。

3. 距離行列を作り直す

4. クラスタが一つになるまで、手順2､3を繰り返す。

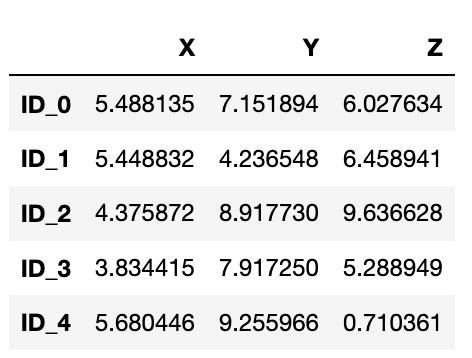
　例として、特徴量を$${X,Y,Z}$$の３個、データポイントを５とした観測値行列を一様乱数を用いて作る。

import pandas as pd
import numpy as np

np.random.seed(0)

F = ['X', 'Y', 'Z']
labels = ['ID_0', 'ID_1', 'ID_2', 'ID_3', 'ID_4']

X = np.random.random_sample([5, 3])*10
df = pd.DataFrame(X, columns=F, index=labels)
df

　このデータフレイムの出力は以下の通りとなる。

df

　このデータポイントの距離行列は、spatial.desitanceのpdistで計算する。

from scipy.spatial.distance import pdist

dist=pdist(df, metric='euclidean')
dist

dist

pdistのmetric引数は、ユークリッド距離だけでなく、ミンコフスキー、マンハッタン距離、シェビチェフ、相関係数などが指定できる。
　出力はarrayであり、これを対称行列として出力させたい時は同じ副モジュールのsquareformを使う。ただし、クラスタリングの距離行列の引数は行列形式でなく、arrayで渡すので、pdistをそのまま渡すのが望ましい。

from scipy.spatial.distance import squareform

dist_mat = pd.DataFrame(squareform(dist),columns=labels,index=labels)
dist_mat

dist_mat

単連結結合アルゴリズムは、scipy.cluster.hierarychyのlincageで実装されている。

from scipy.cluster.hierarchy import linkage
h_cl = linkage(pdist(df, metric='euclidean'), method='complete')

pd.DataFrame(h_cl,
             columns=['cluster p1', 'cluster p2',
                      'distance btw p1&p2', 'no. of dp in clust.'],
             index=[' iteration %d' % (i + 1) 
                    for i in range(row_clusters.shape[0])])

lincageの引数methodは、結合アルゴリズムを指定する。ここでは、completeの完全連結を指定している。対応しているアルゴリズムには、単連結法、平均連結法、ウォード連結法、セントロイド法がある。返り値は、行列で、イテレーション毎の、次のクラスタを構成するクラスタのインデックスとその距離、そのクラスターの中に入っている元々のデータポイントの数が入っている。作成されたクラスタには、データポイント+iterationのインデックスがつけられる。

df h_cl

linkageには、観測行列を渡すこともできるが、その場合は、距離測度を明示する必要がある。

h_cl = linkage(df, method='complete', metric='euclidean')
pd.DataFrame(h_cl,
             columns=['cluster p1', 'cluster p2',
                      'distance btw p1&p2', 'no. of dp in clust.'],
             index=[' iteration %d' % (i + 1) 
                    for i in range(row_clusters.shape[0])])

　結果は当然なことに、pdistを渡した時と同じになる。

　クラスタリングの結果を樹形図で可視化するには、同じモジュールのdendrogramを使う。

from scipy.cluster.hierarchy import dendrogram


row_dendr = dendrogram(h_cl, labels=labels,)
plt.tight_layout()
plt.ylabel('Euclidean distance')
plt.show()

樹形図

対称行列からのlincage

　雑音除去等の何らかの作業で得た対称行列をlinkageの引数としたい場合、上三角行列をとり、非ゼロ成分だけ渡す。

LU=np.triu(dist_mat, k=1)
lu=LU.flatten()
from scipy.cluster.hierarchy import linkage

row_clusters = linkage((lu[lu!=0]), method='complete')
pd.DataFrame(row_clusters,
             columns=['cluster p1', 'clustesr p2',
                      'distance', 'no. of items in clust.'],
             index=['iteration %d' % (i + 1)
                    for i in range(row_clusters.shape[0])])

lu[lu>0]