
BigQuery MLで共変量シフト分析
電通デジタルで機械学習エンジニアをしている今井です。
本記事では、BigQuery MLで共変量シフト分析を行うための方法について紹介します。
拡張配信における共変量の乖離
電通デジタルでは国内外の主要広告プラットフォーマーと協業してさまざまなマーケティング施策に取り組んでおり、その一例が下記のような拡張配信になります。

クライアント企業の保有する購買情報を各プラットフォーマーが保有するユーザーIDと突合することで、そのプラットフォーマーにおける購買期待層への拡張配信を実現するという仕組みです。
通常このような購買情報をプラットフォーマーが直接観測することはできない(例えば店舗来店や継続購買など)ため、事業収益に直結するKPIを基にマーケティング施策を行うのは非常に効果的だと考えます。
上記は理想的な拡張配信になりますが、現実ではID突合に偏りがある場合に適切に購買期待層にアプローチできない可能性があります。
具体的には以下のような状況です。

広告配信ユーザー群と購買観測ユーザー群のそれぞれにおいて男女比率は概ね等しいにも関わらず、ID突合の結果がたまたま男性に偏ってしまったことから、拡張配信に使用する機械学習モデルの学習において男性属性を過大評価してしまい、結果男性にばかり広告が配信されてしまうというものです。
このような機械学習における学習群とテスト群とで共変量(説明変数)に乖離がある状態は共変量シフト(covariate shift)と呼ばれます。
以下ではこの共変量シフトに対応した機械学習のモデル学習手順について紹介します。
Importance Weightによる共変量調整
共変量シフトにおける標準的な学習方法として重要度(Importance Weight)を使用する方法が知られています[1]。
これは観測データを {𝐱𝑖,𝑦𝑖} としたとき、損失関数 ∑𝑖ℓ(𝐱𝑖,𝑦𝑖) の代わりに
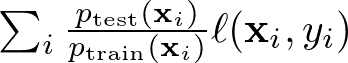
のように重み付けした損失関数を使用するというものです。
ここで 𝑝_test(𝐱𝑖) はテスト群に、𝑝_train(𝐱𝑖) は学習群に割り当てられる確率であり、この重み付けによって共変量の乖離が補正されたモデルを学習できます。
参考までに、この共変量調整は因果推論におけるIPW推定量と同じ考え方です。
IPW推定量については過去記事[2]を一読ください。
ここからはKaggleでも有名なTitanic datasetを使用して共変量シフト分析について紹介します。
手始めに学習/テストで偏りがない場合のモデル精度(log_loss)を確認します。
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import log_loss
df = pd.read_csv('titanic3.csv')
df = df.fillna(df.mean())
# カテゴリ変数は sex のみ使用する
df = pd.concat([df, pd.get_dummies(df[['sex']])], axis=1)
# 男性群において 学習:テスト を 9:1 に分割する
y_ = df.loc[df['sex_male'] == 1]['survived']
df_train_male, df_test_male, _, _ = train_test_split(
df.loc[df['sex_male'] == 1],
y_,
random_state=123,
train_size=0.9,
stratify=y_)
# 女性群において 学習:テスト を 9:1 に分割する
y_ = df.loc[df['sex_female'] == 1]['survived']
df_train_female, df_test_female, _, _ = train_test_split(
df.loc[df['sex_female'] == 1],
y_,
random_state=123,
train_size=0.9,
stratify=y_)
df_train = pd.concat([df_train_male, df_train_female])
df_test = pd.concat([df_test_male, df_test_female])
model = LogisticRegression()
model.fit(
df_train[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values,
df_train['survived'].values)
p_ = [p[1] for p in model.predict_proba(df_test[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values)]
log_loss(df_test['survived'].values, p_)
# 0.43940548903549176このデータには男性/女性はそれぞれ 843/466 名が含まれており、うち生存者は 161/339 名となっています。
そこで、次は女性をテスト群に多く割り当て、学習群の生存確率を低くした場合のモデル精度を確認します。
# 女性群において 学習:テスト を 1:9 に分割する
y_ = df.loc[df['sex_female'] == 1]['survived']
df_train_female, df_test_female, _, _ = train_test_split(
df.loc[df['sex_female'] == 1],
y_,
random_state=123,
train_size=0.1,
stratify=y_)
df_train = pd.concat([df_train_male, df_train_female])
df_test = pd.concat([df_test_male, df_test_female])
model = LogisticRegression()
model.fit(
df_train[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values,
df_train['survived'].values)
p_ = [p[1] for p in model.predict_proba(df_test[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values)]
log_loss(df_test['survived'].values, p_)
# 0.5034738993262718学習群には男性が、テスト群には女性が多くなったことで共変量シフトが起こりモデル精度が悪化しています。
では重要度による重み付けによりこのバイアスを軽減できるかを確認します。
まずは重要度 𝑝_test(𝐱𝑖) / 𝑝_train(𝐱𝑖) を学習します。
df_train['w'] = 0
df_test['w'] = 1
df_iw = pd.concat([df_train, df_test])
model_iw = LogisticRegression()
model_iw.fit(
df_iw[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values,
df_iw['w'].values)
importance_weight = [p[1] / p[0] for p in model_iw.predict_proba(df_train[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values)]次に重要度を反映してモデル学習を行います。
sklearnのLogisticRegressionではfit関数のsample_weightを使用します。
model_iwlr = LogisticRegression()
model_iwlr.fit(
df_train[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values,
df_train['survived'].values,
sample_weight=importance_weight)
p_ = [p[1] for p in model_iwlr.predict_proba(df_test[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values)]
log_loss(df_test['survived'].values, p_)
# 0.4745770716140401重要度でバイアスを補正したことでモデル精度が改善していることがわかります。
ここで重要度による重み付けを実務で使用しているMLツールに適用したいと考えます。
しかしながら、これらのツールでは損失関数を直接指定することができず、sample_weightのような引数も使用できないことがわかりました。
このような状況では重要度による重み付けの代わりに重点サンプリング(Importance Sampling)を使用します。
すなわち損失関数には ∑𝑖ℓ(𝐱𝑖,𝑦𝑖) を使用し、重要度 𝑝_test(𝐱𝑖) / 𝑝_train(𝐱𝑖) によりサンプリングしたデータセットでモデル学習を行うという方法です。
import random
import numpy as np
n_bagging = 5
random.seed(123)
is_p_ = np.empty((n_bagging, len(df_test)))
for i in range(n_bagging):
train_sampling = random.choices(
population=range(len(df_train)),
weights=importance_weight,
k=len(df_train))
model_islr = LogisticRegression()
model_islr.fit(
df_train.iloc[train_sampling][['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values,
df_train.iloc[train_sampling]['survived'].values)
is_p_[i] = [p[1] for p in model_islr.predict_proba(df_test[['pclass','age','sibsp','parch','fare','sex_female','sex_male']].values)]
p_ = is_p_.mean(axis=0)
log_loss(df_test['survived'].values, p_)
# 0.47727354454864607重点サンプリングを使用しても同程度にバイアス補正できていることがわかります。
なお、サンプリングによる不確実性を軽減するために複数のデータセットによるモデル学習を行っていますが、これはBaggingと呼ばれる機械学習手法となります。
BigQuery MLで共変量シフト分析
最後にBigQuery MLによる共変量シフト分析について紹介します。
なお、学習/テスト/重点サンプリングのデータセットについては上記のPandas DataFrameを直接BigQueryにインポートして使用しています。
モデル学習についてはすべて以下のコードを使用します。
#standardSQL
CREATE OR REPLACE MODEL
`dataset_id.model_name`
OPTIONS(
MODEL_TYPE="logistic_reg",
input_label_cols=["survived"],
max_iterations=50,
early_stop=false,
l1_reg=0.01
) AS
SELECT
survived,
pclass,
age,
sibsp,
parch,
fare,
sex
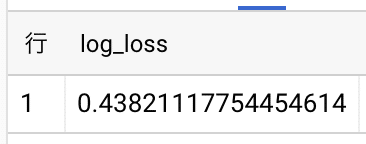
FROM `project_id.dataset_id.train_table`はじめに男女比のバイアスがないデータセットで学習したモデルを評価します。
#standardSQL
SELECT
log_loss
FROM
ML.EVALUATE(MODEL `dataset_id.model_name`, (
SELECT
*
FROM
`project_id.dataset_id.test_table`
)
)
次に男女比のバイアスがあるデータセットで学習したモデルを評価します。
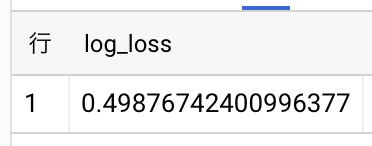
では重要度による重点サンプリングで作成した複数のデータセットでモデル学習します。
なお、複数モデルに対して ML.EVALUATE は使えないため、代わりに以下のコードでモデル評価を行います。
#standardSQL
WITH predict_0 AS (
SELECT
survived,
CONCAT(name, '-', ticket) AS unique_id,
predicted_survived_probs[OFFSET(0)].prob AS p_survived_0
FROM
ML.PREDICT(MODEL `dataset_id.model_0`, (
SELECT
*
FROM
`project_id.dataset_id.test_table`
)
)
),
predict_1 AS (
SELECT
CONCAT(name, '-', ticket) AS unique_id,
predicted_survived_probs[OFFSET(0)].prob AS p_survived_1
FROM
ML.PREDICT(MODEL `dataset_id.model_1`, (
SELECT
*
FROM
`project_id.dataset_id.test_table`
)
)
),
...
),
bagging AS (
SELECT
(p_survived_0 + p_survived_1 + p_survived_2 + p_survived_3 + p_survived_4) / 5 AS p_survived
FROM predict_0
LEFT JOIN predict_1 USING (unique_id)
LEFT JOIN predict_2 USING (unique_id)
LEFT JOIN predict_3 USING (unique_id)
LEFT JOIN predict_4 USING (unique_id)
)
SELECT
AVG(- survived * LOG(p_survived) - (1 - survived) * LOG(1 - p_survived)) AS log_loss
FROM bagging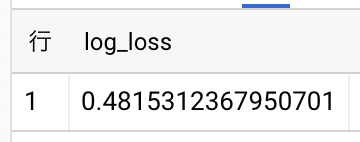
概ねsklearnと同じ結果になっていることがわかります。
多くのAutoMLツールではBigQuery MLと同様に損失関数を指定できないため、重点サンプリングによる共変量調整を行うことになります。
一方で、例えばGCP AutoML Tablesでは「Weight column」を指定できるため、重要度による重み付けにより共変量シフトに対応することができます。
AutoMLはデータセットを用意して最適化指標などのパラメータを指定するだけで、高精度なモデリングに必要となる特徴量エンジニアリングやパラメータチューニングなどを自動で実行して機械学習モデルを構築してくれますが、先述のように適切なデータ分析設計になっていなければ意味のない分析となってしまいます。
ただ単に高精度なモデルを最低限の開発工数で作成するというだけではなく、データ分析設計に応じて適切にMLツールを使いこなせることが今後の機械学習エンジニア/データサイエンティストにとっての試金石になるかと思われます。
参考文系
[1] Shimodaira, Improving Predictive Inference under Covariate Shift by Weighting the Log-Likelihood Function, 2000
[2] BigQueryで傾向スコア分析
