時系列性を考慮した因果探索手法VAR-LiNGAMの紹介
電通デジタルでデータサイエンティストをしている中嶋です。
この記事では、これまで紹介したLiNGAMの派生形であるVAR-LiNGAM（Vector AutoRegression-LiNGAM）について紹介したいと思います。これは通常のLiNGAMにベクトル自己回帰モデル(Vector AutoRegression Model: VAR Model)の考え方を取り入れ、時系列性の因果も考慮した因果探索を行うものです。
今回の記事では分量の関係からGoogle Colabでの実装は割愛し、元論文[1]を参考にしながら主に理論的な部分の紹介を行います。
定式化
VAR-LiNGAMの定式化を説明する前に論文の形式に倣ってまずはLiNGAMとVARそれぞれの定式化をおさらいします。個別の説明に入る前に全体像を以下に示します。
LiNGAM
LiNGAMとはLinear Non-Gaussian Acyclic Modelの略で因果探索のセミパラメトリックなアプローチの手法の一つです。LiNGAMの一般的な定式化は以下になります。
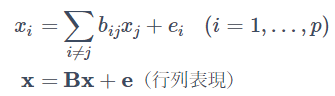xi,ei (i=1,...,p) はそれぞれ観測変数、外生変数を表し bij (i,j=1,...,p) は因果係数を表します。2つ目の式は1つ目の行列表現となっており、
で、 B は (i,j) 要素が bij の p×p 行列を表します。構造方程式モデル（Structural Equation Model：SEM）と似ていますが、外生変数に非ガウス分布を仮定しているのが特徴です。
VARモデル
ベクトル自己回帰モデル（Vector AutoRegression Model: VAR Model）の略で、時系列分析で使われるモデルの一つです。現時点のベクトル化された時系列 x(t)=(x1(t),...,xp(t))T を過去 k 時点の時系列 x(t−τ)=(x1(t−τ),...,xp(t−τ))T (τ=1,...,k) の線形和として表したモデルです。定式化は下記のようになります。
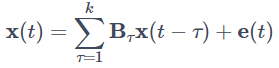ここで Bτ は過去時点 t−τ から現在の値への直接的な影響を表す係数となっています。通常の自己回帰モデル（Auto Regression Model: AR Model）では変数が一つなので過去の自分自身のデータのみを説明変数にして線形モデリングしますが、VARでは自分自身だけでなくインデックスの異なる時系列xj(t−τ),τ=1,2,...も含めてxi(t)の予測を行います。
上記を踏まえてVAR-LiNGAMのモデル式を説明します。
VAR-LiNGAM
上記の2つのモデルを組み合わせて下記のイメージ（ここでは例として x1(t−1)→x3(t),x2(t−1)→x2(t),x1(t)→x2(t) という因果を想定しています。）のように過去からの因果効果も含めて因果モデルを構築することを考えます。
一般的な定式化としては下記のようになります。
上記のVARモデルとかなり似た形をしていますが、時間差を表すτが0から始まっている点に注意してください。B0は、LiNGAMのBのように現時点の他変数からの因果を表す係数で、 Bτ (τ=1,...,k) は過去時点の x(t−τ) からの直接的な影響を表す係数です。これにより現在のベクトル変数の値 x(t) を現時点の他の変数だけでなく過去時点のベクトル変数も用いて推定することができ、時系列性を踏まえた因果グラフを作ることが可能となります。
VAR-LiNGAMにおける仮定を下記に列挙します。
1. ei(t)は変数間で独立で、時間的にも独立である。
2. ei(t)が従う分布は非ガウス分布である。
3. B_0 が表す因果グラフは非巡回グラフとなる。
このモデルの識別性（このモデルを用いることで観測データから因果グラフを一意に特定できるか）には2. の非ガウス性が効いてきます。VAR-LiNGAMと似たモデルとして、構造VARモデル(Structural VAR model)というものがありますが、撹乱項 e(t) の非ガウス性の仮定が決定的に異なります。
・構造VARモデル(Structural VAR model)
同時点の変数が互いに及ぼす影響を明示的に取り入れたVARモデル。一般式は下記の通り。
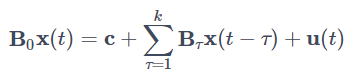ここで B0 は対角成分が全て1の n×n 行列で、u(t) はホワイトノイズとする。
また3. の非巡回性の仮定は必ずしも要るものではないことが元論文[1]で述べられています。
モデルの推定方法
ここでは上記で定式化したVAR-LiNGAMの推定方法について説明します。
元論文[1]では3種類の方法が紹介されています。この記事では、最初にVARモデルとしての推定を行ったのちに通常のLiNGAMモデルの推定を行う2段階法について紹介します。
それ以外の方法については概要だけの紹介にとどめます。詳細については元論文[1]及び参考文献[2]をご参照ください。
最小二乗推定を用いた2段階法
- 着想
まず最初にどのようにして2段階法ができるかを元のモデル式を変形して説明します。
最初に右辺の和の部分を τ=0 と τ>0とに分けます。
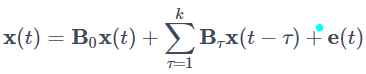右辺第一項を左辺に持ってきて、両辺を I−B0 で割ります。I−B0 が逆行列を持つことは前述の定式化で述べた仮定3. によって保証されます。
ここで
と置くと、上式は
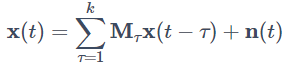となり、これはVARモデルの式と同じに形になります。よって通常のVARモデルの推定と同様にしてこの式の Mτ ,n(t) を推定することができます。一方(4)式を変形すると
となり、これはn(t) に対するLiNGAMそのものになっているので B0 の推定ができます。
よって、Mτ, B0を(4)式に代入することで Bτ を求めることが可能となります。
- 実際の推定手順
上記の着想を基に(1)式における Bτ の推定手順を整理します。
1. VARモデルの推定
まず、時系列ベクトル x(t) に対する通常のVARモデルを下式のように構築し、最小二乗推定量 M^τ を計算します。
2. VARモデルの残差の推定
M^τ を上記の(5)式に代入することで撹乱項の推定値 n^(t) を計算します。数式として書くと下記のようになります。
3. 残差に対するLiNGAMモデル推定
n^(t) に対する下式のLiNGAM推定を行います。これにより因果係数行列の推定値 B^0 が求まります。
4. VAR-LiNGAMの推定
1.で求めた M^τ と 3.で求めた B^0 から、(3) 式を参考にした下記の式によりB^τ を求めます。
- 推定量の一致性
※このパートに関しては本手法の実データ適用においてはあまり関係ない部分なので、読み飛ばしても問題ありません。サンプル数を大きくすると正しい値に収束することが理論的に保証されているという点だけ抑えていただければ結構です。
この二段階法における推定量 B^τ には一致性があることが元論文[1]の中で示されています。ここで一致性とは標本数が大きくなった時に推定量が母数に限りなく近づくことを言います。以下一致性がどのようにして得られるかを簡単に説明します。
まず(5)式のVARモデルの最小二乗推定に関するよく知られた結果として、撹乱項 n(t) が（固定された t に対して）独立でないあるいは無相関でない場合や、不均一分散で非ガウス分布であったとしても、推定量 M^τは一致性を持つということが知られています。これにより(2)式と(5)式で x(t−τ) の係数及び残差をそれぞれ比較することで、漸近的に
という関係式が得られます。一方 B0 に関しては、上記の(9)式を(7)式のように式変形することで n^(t) に対するLiNGAM推定量として得られ、この推定量にも一致性があることが示されています。
よって、上記(8)式と推定量 M^τ,B^0の一致性からB^τ (τ=1,...,k) の一致性が得られることを踏まえると、全てのB^τで一致性があることが示されました。
MBDに基づく方法
マルチチャネルブラインドデコンボリューション（Multichannel Blind Deconvolution: MBD）とは、以前紹介したLiNGAMモデルの推定法の一つである独立成分分析（Independent Component Analysis: ICA）の畳み込み版ともいえる手法です。私自身もこの用語は元論文[1]で初めて知ったのでこれ以上の詳細な説明はできないのですが、調べたところ信号処理分野でのブラインド音源分離（Blind Source Separation: BSS ）に関する手法のようです。このMBDを使うと、詳細は割愛しますが、VAR-LiNGAMの定式化のところで出てきた撹乱項e(t) を
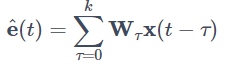として表すWτを推定することができ、これにより、Bτが復元できます。
スパース正則化MBD
上記で紹介したMBDにおいて最適化する指標（対数尤度logL(Wτ)）に、適応的L1罰則項を追加することで高次元のデータに対しても対応できるようにしたものです。特に、過去の観測値から現在の観測値への総合効果の推定のためにグループLassoを併用する方法もあり、適応的L1罰則項と合わせて下記のような尤度を最適化します。
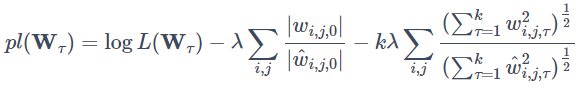上記の右辺第二項が適応的L1罰則項で、右辺第三項がグループLassoによる罰則項です。対数尤度最大化なので罰則項にはそれぞれマイナスが付いています。
以上VAR-LiNGAMの推定法として2段階法、MBD、スパース正則化MBDについて紹介しました。元論文[1]のシミュレーションではスパース正則化MBDが最も係数の推定を正しく行うことができることが示されています。
係数の有意性検定
VAR-LiNGAM含めLiNGAMの手法において推定された因果係数が0と有意に異なるかどうかは重要な論点です。しかしながら現状は因果係数の漸近分散について明らかになっていることはあまりありません。そこで通常はブートストラップサンプリングを用いて係数の経験分布を求めることで有意性を確認します。（例えば、BMLiNGAMの記事の実装パートの最後に提示した事後分布があります。）
ここでは、分散を表すシンプルな統計量を提案しそれを用いて仮説検定を行う方法を紹介します。
分散統計量
τ=0 の場合（同時因果効果）と τ>0 の場合（過去からの因果効果）に分けて説明します。
・同時因果効果の係数の分散統計量
xi(t) からxj(t)への同時因果効果を表す係数の分散統計量を次の式で定義します。
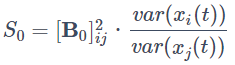
・過去からの因果効果の係数の分散統計量
過去からの因果効果を検証する際は、通常ある一つの τ>0 のみでの効果には関心はなく τ>0 全体での因果効果を見ることが多いです。よって xi(t−τ),τ>0 から xj(t) への総合的な因果効果の分散統計量を次の式で定義します。
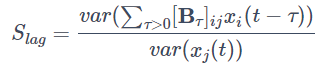
検定方法
因果係数が0という帰無仮説の下での各統計量の経験的分布を求めるために、サロゲート法によるブートストラップを用います。具体的に言うとブートストラップのときに元の系列 xi(t) の時間的順序をランダムに並び替えたものをサンプリングします。ここでは因果効果が無いという帰無仮説から各 xi(t) は残差項だけが残り、各時刻でi.i.d.なデータとみなせることを暗に用いています。これによって得られたサロゲートデータから統計量 S（=S0 または Slag）の推定値である S∗^ を計算します。（* はブートストラップからの統計量であることを表します。）
そしてブートストラップから得られるS∗^の分布の上位 α 分位点 c∗top α を求め、元データから算出した S^ がこれを超えれば帰無仮説を棄却します。
VAR-LiNGAMの因果効果のGranger因果的解釈
VAR-LiNGAMにおける過去からの因果と、時系列分析の文脈で登場するVARモデルにおけるGranger因果は若干の相違があります。このパートではこれら2つの時系列因果の差異及び共通点を説明し、より一般的なGranger因果を定義することを試みます。
同時因果効果が過去からの因果効果へ与える影響
まず最初に、同時因果効果を考慮しないVARモデルによって因果係数の推定が変化してしまうケースを紹介します。
- 同時因果効果が過去からの因果効果として現れてしまうケース
2つの時系列 x1(t),x2(t)があり、x2→x1の同時因果効果と自身の時系列のラグ1の過去からの因果のみがあるものと想定します。具体的には同時因果効果の係数行列 B0 とラグ1の過去からの因果効果を表す係数行列 B1 が下記のようになっているケースを考えます。
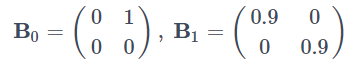この時、同時点の因果効果を考慮せずにAR(1)モデルを推定すると(9)式から
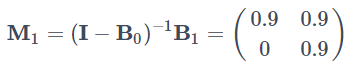となり、同時因果効果が過去からの因果効果して現れてしまいます。
- 本来存在しない因果効果が出現してしまうケース
今度は３つの時系列 x1(t),x2(t),x3(t)があり、 B0 と B1 が下記のようになっているケースを考えます。
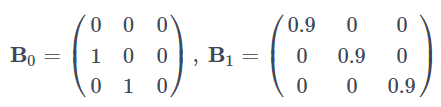このモデルから得られるデータに対して先ほどと同様にAR(1)モデルを当てはめると、
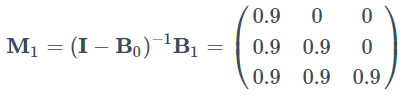となり、データを生成するモデルでは存在しなかった過去からの因果効果 x1→x3 が出てきます。
このように、VAR-LiNGAMで想定しているような同時因果が存在する場合に通常のVARモデルを用いてしまうと、同時因果が過去からの因果として出てきてしまうことがあります。こうなると因果の向きも逆になってしまうことがあるのではないかと思われるかもしれませんが、そうではないことが次の定理によって保証されています。
・定理（VARモデルとVAR-LiNGAMで因果順序を保持するための条件）
(1)式の Bτ, τ≥0 に関して同時点と全ての時間ラグで矛盾しない因果順序がある場合、VARとVAR-LiNGAMで因果順序が逆転することはない。（ただし因果の係数は上記で見たように変わる可能性がある。）
上記の仮定の意味するところとしては、例えばx1(t)→x3(t)という同時因果があった場合、過去からの因果としてx3(t−τ)→x1(t)は存在しないこと、また x1(t−τ)→x2(t), x2(t−τ)→x3(t) はあり得ることを述べています。結論部分は同時点の因果効果を無視しても因果順序自体は変わらないことを意味しています。証明ですが、同じ因果の順序があるということを Bτ, τ≥0が全て下三角行列になることと言い換えることで、下三角行列の性質により証明できます。
Granger因果の一般化
上記の考察から因果の順序自体は変わらないことが分かったので、これを踏まえて古典的なGranger因果の考え方を VAR-LINGAMでの因果にも適用できるように拡張してみます。まずGranger因果について簡単に説明します。
・Granger因果
時系列分析における因果の考え方は少し特殊で、因果性を予測誤差を減らせるかどうかで定義しておりこれをGranger因果と呼びます。具体的に言うと2つの時系列 x1,x2 があった時に、 x1 の予測に x2を説明変数として入れることで予測誤差が減るならば、x2→x1 のGranger因果があると言います。
VAR-LiNGAMの状況では xi(t−τ), τ≥1 から xj(t) までの係数のうち少なくとも 1 つが（有意に）非ゼロである場合、xi は xj をGrangerの意味で引き起こす原因となります。これは、変数 xi が説明変数の集合に含まれている場合 xj の平均二乗予測誤差を減少させるからです。これを踏まえてより一般的なGranger因果を下記のように定義します。
・一般化Granger因果
τ≥0 について xi(t−τ) から xj(t) への効果を与える係数Bτ(j,i) の少なくとも1つが、（有意に）非ゼロである場合に、一般化Grangerの意味で xi→xj という因果があると定義する。
同時因果効果に対応する τ=0 の場合が含まれているので、τ の条件は通常のGranger因果性とは異なります。また、同時因果効果の推定によって過去からの因果効果の推定値が変化するため、この定義における過去からの因果は通常のGranger因果とは異なります。
実応用事例
折角なので実際にどのようにVAR-LiNGAMが使われるかを事例を通して紹介したいと思います。このパートで紹介する事例はできるだけマーケティングの実務に近いものにしたかったため、元論文[1]ではなく事例論文[5]を参考にしました。詳細が気になる人はそちらも参考にしてください。
ミクロ経済学での企業成長分析
この事例ではアメリカの企業の売上推移がどのような要因で成長しているかをVARモデルとVAR-LiNGAMで分析して、特に過去からの因果について比較検証したものです。
- 使用したデータ
この分析では米国の証券取引所に上場している米国企業を対象としたCompustatデータベース（参考文献[6]）を使いました。1973年から2004年までの製造業（SICクラス2000-3999）企業を対象に、従業員（Empl）、総売上高（Sales）、研究開発費（RnD）、営業利益（OpInc）の変数の年次推移を取得しています。
前処理として、各企業が年次報告書などで重要でないと明言している変数については、手動で0にするようにしています。（研究開発費と営業利益に該当するものがあったと思われます。）また時系列はそのままを用いずに t 年の会社 i における成長率を表す対数時系列
を使っています。後の結果では元の時系列の変数と区別するために（.gr）という接尾辞が付いています。対数時系列を作る関係で、各年の営業利益、研究開発費、および従業員は正の値を取るもののみに絞りました。これによって特に営業利益のデータは15%程度減っています。
- 結果
下記の表に(a)VARモデルによる過去からの因果係数、(b)VAR-LiNGAMによる過去からの因果係数の推定結果をまとめます。観測値の総数は28,538件あり、太字の係数は有意水準0.01でのt検定により有意に0でないものです。また、表は列から行に読むように配置されており、例えば、VARによる売上高成長（Sales.gr）→雇用成長（Empl.gr）の1時点前からの因果係数は0.1017となります。
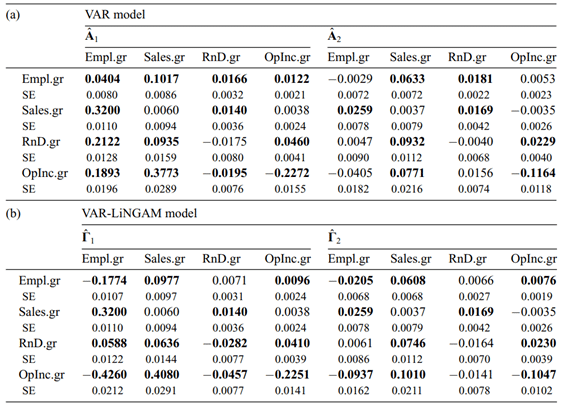VAR-LINGAMの同時因果係数の推定結果は下記になります。表の見方は上表と同じです。
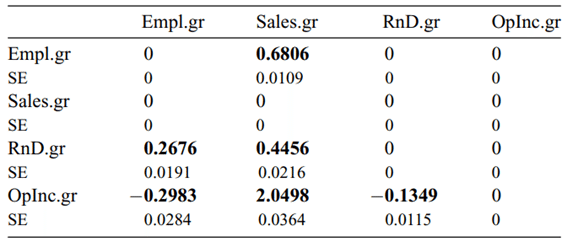最初の表の(b)と二つ目の表からVAR-LINGAMの因果グラフが下記のように得られます。実線の矢印は正の効果、破線の矢印は負の効果を示しており、太い線は強い効果、細い線は弱い効果に対応しています。
- 考察
最初の表を見ると、(a)VARモデルでは雇用成長（Empl.gr）が1時点後の利益成長（OpInc.gr）に正の効果（0.1893）があることを示していますが、対応する(b)VAR-LiNGAMでは強く負の効果（-0.4260）が出ています。これについては下記のような説明ができます。
VAR-LiNGAMでは（雇用は人件費コストとなることから）利益に対する雇用による直接的な負の効果（Empl.gr(t+1)→OpInc.gr(t+2)）と、t+1時点の雇用成長（Empl.gr）がt+2時点の売上高の増加（Sales.gr）を通じてt+2時の利益増加（OpInc.gr）につながるという間接的な正の効果（Empl.gr(t+1)→Sales.gr(t+2)→OpInc.gr(t+2)）とが分かれており前者の部分だけが負の効果として出ています。一方VARモデルではそれらが分離されておらず総合効果としてしか現れていないため、結果としてこのような差が出ているものと思われます。
このように通常のVARモデルでは分離できなかった同時効果の影響がVAR-LINGAMを使うことで切り分けることができます。実務においてはここで紹介した例以外にもマス広告による売り上げへの影響を調べるためにVARモデルを使ってGranger因果等を調べたりすることもあると思います（参考文献[7]）が、今回紹介したVAR-LINGAMを使うことでより正確な因果グラフを推定することができそうです。
最後に
この記事では以前紹介した因果探索手法LiNGAMをVARモデルと組み合わせることで、時系列の因果を考慮した因果探索ができることを示しました。
モデルの推定方法にはいくつか種類があり、素朴な方法として2段階法を紹介しました。この方法による推定量は一致性を持っています。
推定された因果係数の有意性検定のために簡単な分散統計量を提案し、ブートストラップ法を用いて検定する方法を紹介しました。
最後にVAR-LiNGAMの意味での過去からの因果と時系列分析で登場するGranger因果の違いを説明しGranger因果を一般化した定義を提案しました。
元論文[1]では他にも撹乱項が非ガウスであることの妥当性や、最適化する目的関数（対数尤度）の導出と情報理論との関連についても触れられていますが、込み入った話になるため割愛しました。
今回紹介しきれなかった実装については参考文献にRとPythonのライブラリを載せておりますので、もし興味があれば使ってみてください。
参考文献
・VAR-LiNGAM論文
本記事で紹介したVAR-LiNGAMの元論文です。
Estimation of a Structural Vector Autoregression Model Using Non-Gaussianity
[1]https://www.jmlr.org/papers/volume11/hyvarinen10a/hyvarinen10a.pdf
・畳み込み混合のブラインド音源分離
本記事と直接は関係ないですが、推定方法のところで触れたMBD（マルチチャネルブラインドデコンボリューション）が登場する記事です。
[2]https://www.tara.tsukuba.ac.jp/~maki/reprint/Makino/sm04iscie401-408.pdf
・R実装
[3]https://sites.google.com/site/dorisentner/publications/VARLiNGAM
・Python実装
リンク先にある別の手法ではVAR-LiNGAMに移動平均項を追加したVARMA-LiNGAMというものもあります。
[4]https://lingam.readthedocs.io/en/latest/tutorial/var.html
・VAR-LINGAMによる分析事例
記事内で紹介した事例について書かれている論文です。
Causal Inference by Independent Component Analysis: Theory and Applications
[5]https://www.iris.sssup.it/retrieve/handle/11382/355635/1330/j.1468-0084.2012.00710.x.pdf
・事例で使われたデータ
上記の論文で紹介されているCompustatデータセットは下記のWharton Research Data Servicesでアカウントを作成すると取得できるようです。
[6]https://wrds-www.wharton.upenn.edu/
・VARモデルによる因果推論
通常使う因果とは言葉の意味が異なりますが、時系列データでの因果を推定する事例として紹介します。
[7]https://www.ieice.org/publications/conference-FIT-DVDs/FIT2019/data/pdf/O-020.pdf