
#4 データを見やすくすると伝わりやすくなる
ここまで、ロト7のデータベースを使って本数字の当せん番号を軸に大まかな特徴をつかむために、合計、平均、中央値を出したり、仮説検証を行ったりしましたが、自分だけが見るには構いませんが、例えば人に見せる場合に数字が苦手な相手には伝わりにくいのではないかと思います。
そんな人に数字のたくさん入った表を一生懸命に説明しても思いは十分に伝わりません。分かりやすく説明するために、ビジュアル化するのが一つの方法です。
難しく考える前に、まずはExcelで作った表にグラフを添えるところからはじめるといいかと思います。
自分が見たいもの、見せたいことが正しく伝わるもの。ができると私は自身の中に次はこれが知りたい、あれ知りたいという欲求が生まれてきます。
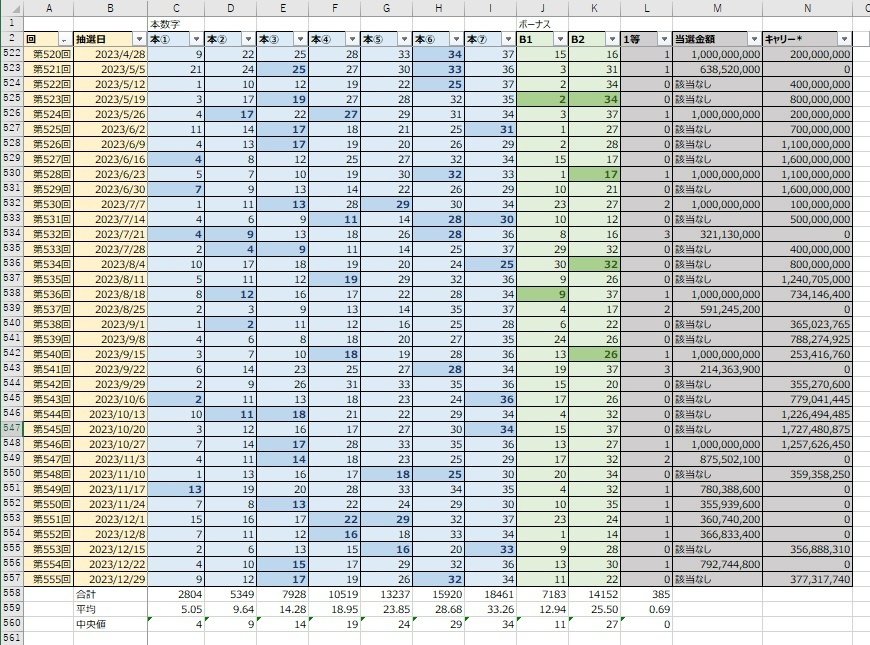
これは、以前の記事で使用した画像ですが、ロト7の結果を第1回から順に並べているにすぎません。これはこれで各回の結果を詳細に知ることができる。と言う目的を達成しています。
次の欲求が本数字ごとの合計、平均、中央値でしたが、それぞれどの数字が多く出ているのか気になりませんか?
平均は合計を個数で割った慣らした数字、中央値は最大と最小から順番が真ん中にくる数字です。極端な話をしますと、最大最小に偏ったもの、真ん中に偏ったもの、まんべんなく均等なもの。それぞれ中身は異なりますが、平均や中央値は同じになる可能性があることを理解しないといけません。
まずは、本数字①~⑦(今回はボーナス①②も)の当せん番号を1~37の番号ごとに集計してみます。
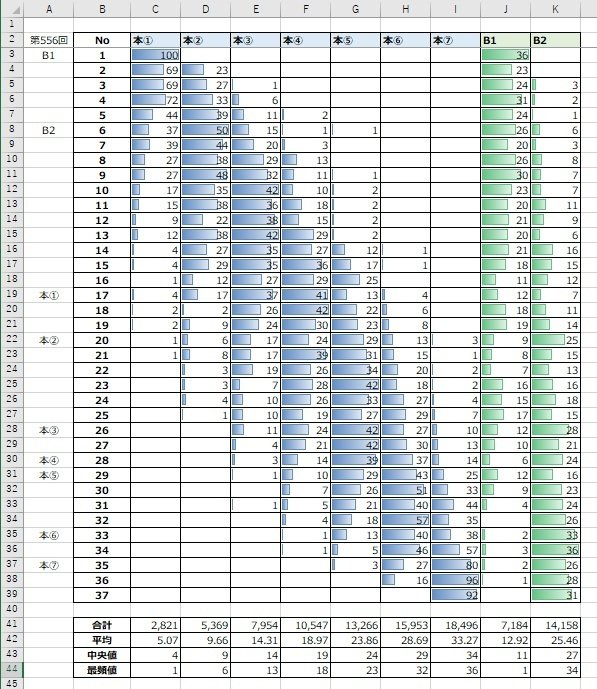
分かりやすくするために、条件付き書式という便利な機能がExcelにはありますので、セルの中に入った数字を棒グラフにしてみました。
そうすると、一目瞭然です。本数字①は全556回のうち1が100回も出ています。本数字②以降は前の本数字に影響されるので、大きく偏って出現している数字はなさそうです。だから当てるのが難しいんですね。
こちらの表を作成するには、前回のCOUNT関数の説明時に記載した『少し難易度が高めのCOUNT関数に条件を付けたもの』を使っていますが、構造を理解すれば難しくありません。
つまり、C3のセルには個数を数えるCOUNT関数に対し、『本数字①の中で当せん番号1だけ数える』と言う条件をつけた関数が入っていて、C4には『本数字①の中で当せん番号1だけ数える』と言う関数が入っています。
これが、C3からK39まですべてに入っています。
使用したExcel関数は COUNTIFS関数です。
=COUNTIFS(①,②) ①が範囲、②が条件でこの2つをカンマ , で区切って1セットです。=COUNTIFS(①,②,③,④,⑤,⑥,⑦,⑧)と条件が増えても問題ありません。その場合は③④がセット、⑤⑥がセット、⑦⑧がセットになります。
IFはExcelで条件指定をする意味合いですので、COUNTIFで条件付きで数える関数になります。COUNTIFSはIFに複数形のSがついたもので、複数条件にも対応可能な関数です。
COUNTIF関数は条件が1つしか使えないので、こちらは覚える必要がありません。COUNTIFS関数で条件が1つだけの場合にも対応できます。
ロト7のデータにあてはめてみるとこのようになります。
=COUNTIFS(表1C:C,表$B:$B)
表1が結果を羅列した表が入っているシートで、
表2が本数字と当せん番号で数字を集計する表が入っているシートです。
表1C:C 結果を羅列した表のC列 ・・①
表2$B:$B 本数字と当せん番号で数字を集計する表のB列 ・・②
今回は条件が1つなので、シンプルな関数になりますが、非常にな関数なので、これは『あんなことができたはず』でなく、絶対に覚えた方がいいです。必ずあなたの武器になります。
今回はヒストグラムに近いものを関数を使って作成しました。
ヒストグラムとは数値を区間ごとに度数分布をグラフで表現したものです。
この一連の作業を『データの可視化(データビジュアライゼーション)』と言い、データの可視化するためには非常に有効な手段になります。
最後に、それぞれ当せん番号ごとに集計し出現回数を集計しましたが、Excelには便利な関数があり、最頻値を目視でなく、関数で求めることができます。最頻値とは、最も頻繁に出現する値です。
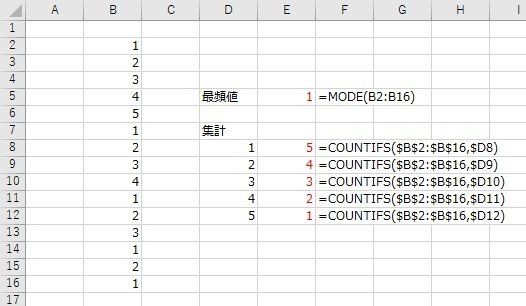
B列に入った1~5までの15個の数字の最頻値は・・・
=MODE(B2:B16) で出してくれます。
COUNTIFS関数で1から5までそれぞれ集計した結果も載せましたが
1が5個で一番多くなっているのが確認できますでしょうか。
今回は以上です。
関数の中に$ドルマークが入っていますが、これはExcelに慣れていく上で非常に便利な記号です。またの機会で説明しますね。
今回はグラフまで辿り着けませんでした。次回、同じデータを使ってグラフ作成をします。
※表2の表に入っている合計の値は回数と出た目の値を掛けたものになっていますので、SUM(C3:C39)の結果とは異なります。
