
ゼロからはじめる変分オートエンコーダ:理論からTensorFlow実装、可視化、応用まで完全理解
はじめに(この記事の全体像)
※現在、記事作成中のため、ファクトチェックができていない部分がありますので、ご了承ください。
本記事では、初学者の方が理解に苦しみがちな「変分オートエンコーダ(Variational Autoencoder、以下VAE)」について、理論的背景からTensorFlowによるプログラム実装、図を用いた可視化まで一貫して解説します。教科書やウェブサイトでは難解な数式や用語が頻出する一方で、具体的な実装例やわかりやすい説明が不足していることも多く、初学者にとって理解のハードルが高くなりがちです。
本記事では、数学的な式や用語を、初心者にもわかるような段階的・直感的な説明を交えながら整理します。その上で、実際にTensorFlow(Keras)でVAEを実装するコード例を提示し、matplotlibによる図示で理論と実践を結びつけます。このプロセスを通じて、ただ理論を知るだけではなく、実際に手を動かして検証しながら「VAEが何をやっているか」を腑に落とすことができるようになります。
この記事を読むことで得られる価値は以下の通りです。
わかりやすい段階的説明:基礎的なオートエンコーダ(AE)の仕組みから始め、VAEがどのように確率的な潜在変数モデルとして拡張されるのか、数式を用いつつ噛み砕いて説明します。
理論と実践のリンク:理論解説と同じパートでTensorFlowコードを示し、さらに学習結果を可視化することで、読者は理論が単なる抽象概念でないことを実感できます。
応用可能な理解:VAEを用いて潜在空間から新たな画像を生成したり、データ拡張、異常検知、さらにはサービス開発につなげるヒントを得ることができます。
この記事を通じて、VAEの本質的な理解を深め、サービス開発まで見据えた応用力を身につけていただければ幸いです。
目次
変分オートエンコーダ(VAE)とは何か?
オートエンコーダの基本的な仕組み
VAEが解決する課題と特徴
従来のAEとの違いとVAEの全体的な流れ
VAEの理論的背景
潜在変数モデルとは?(潜在的な要因を捉える考え方)
エビデンス下界(ELBO)とKLダイバージェンス
再パラメータ化トリック(Reparameterization Trick)の直感的理解
VAEの数式解説
損失関数(ELBO)の導出過程と意味
確率的エンコーダ・デコーダとガウス分布の役割
従来のAEとの数学的な違い
VAE実装への準備
必要なライブラリ(TensorFlow、matplotlib、numpy)
データセット準備(MNIST)
モデル設計の概要(エンコーダ、デコーダのアーキテクチャ)
VAEのTensorFlow実装(ステップバイステップ)
エンコーダ・デコーダクラスの定義
再パラメータ化による潜在変数サンプリング
ELBO損失関数の実装
トレーニングループの記述
学習結果の可視化と検証
再構成画像の表示(元画像との比較)
潜在空間の可視化(2次元化した場合の例)
潜在変数からの新規サンプル生成の例
応用例とサービス化へのヒント
データ拡張、異常検知、潜在空間による検索・生成サービスアイデア
発展モデル(CVAE、Beta-VAEなど)の紹介
まとめと今後の学習指針
1. 変分オートエンコーダ(VAE)とは何か?
オートエンコーダ(AE)の基本的な仕組み
オートエンコーダ(Autoencoder)は、入力データ(例えば28×28ピクセルの手書き数字画像)を一度、低次元の「潜在空間」へ圧縮(エンコード)し、その潜在変数から元のデータを再構成(デコード)するモデルです。これにより、データの重要な特徴を抽出したり、ノイズ除去を行ったりできます。
たとえばMNIST画像(手書き数字)を考えると、オートエンコーダは28×28=784次元のピクセル値を、わずか20次元程度まで圧縮します。再構成がうまくいくなら、この20次元が「数字を表現する本質的な情報」を持っていると考えられます。しかし、通常のAEでは、この潜在空間上の点を自由に移動しても「意味のあるデータ」が常に得られるとは限りません。
VAEが解決する課題と特徴
変分オートエンコーダ(VAE)は、潜在空間を確率的な分布としてモデル化します。つまり、単なる「点」ではなく、「分布」から潜在変数をサンプリングする仕組みを導入しています。この分布をうまく学習することで、潜在空間が「常に意味のあるデータ生成」を保証するようになります。結果として、VAEは「新しいデータを生成する能力」を獲得します。
ここで「意味のあるデータ」とは、訓練データに類似した性質を持つ新規サンプルが潜在空間から自然に得られることを指します。たとえばVAEをMNISTで学習すると、潜在空間上でランダムに点をサンプリングしてデコーダに通すと、新しい手書き数字が「自然に」生成できるようになります。
従来のAEとの違いとVAEの全体的な流れ
従来のAE:
入力 → 潜在空間(1つの潜在ベクトル) → 復元
損失は主に再構成誤差(元の画像と出力画像の差)VAE:
入力 → 潜在分布(平均と分散)→ この分布からサンプリングした潜在変数で復元
損失は「再構成誤差+潜在分布と事前分布の差(KLダイバージェンス)」
これにより潜在空間が統計的に整った構造を持つ
VAEでは、エンコーダが潜在空間の「平均」や「分散」といったパラメータを出力し、その分布からサンプリングしてデコーダに入力します。そのため潜在空間上で自由に点を移動しても、常に「それっぽい」データが得られやすくなるのです。
2. VAEの理論的背景
潜在変数モデルとは?
潜在変数モデルとは、観測されるデータ(画像など)の背後に、観測できない潜在的な因子(潜在変数)が存在し、それを用いてデータが生成されていると考えるモデルです。たとえば「ある数字を書く」という行為の背後には「書き手の意図」「数字の形状の特徴」といった潜在的な要因があります。VAEでは、この潜在変数を確率分布として扱い、データ生成過程を「潜在変数をまずサンプリングし、その潜在変数に基づいてデータを生成する」というストーリーで描きます。
エビデンス下界(ELBO)とKLダイバージェンス
VAEの学習は、観測データの分布をうまく説明する潜在分布を求めることに相当します。しかし直接それを扱うのは難しいため、**ELBO(Evidence Lower BOund)**という指標を最大化(あるいは負号を付けて最小化)します。
ELBOは、観測データ xx に対して以下のように定義されます。
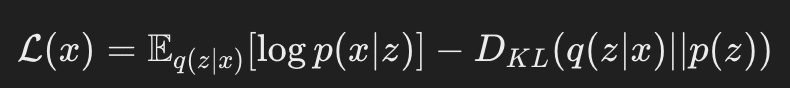
ここで、
q(z∣x)q(z|x) はエンコーダが学習する近似分布(潜在変数 zz が入力 xx によってどのような確率分布を持つかを表す)
p(z)p(z) は潜在変数の事前分布(通常は標準正規分布を仮定)
p(x∣z)p(x|z) はデコーダが表す生成分布(潜在変数 zz から元のデータ xx を生成する確率)
「D.KL」はKLダイバージェンスと呼ばれる二つの確率分布間の距離を測る指標で、0以上の値を取ります。
ELBOを最大化すると、「元のデータを再構成する精度を上げつつ、潜在分布が標準正規分布に近づく」ような学習が行われます。これにより、潜在空間が滑らかで連続的な構造を持ち、生成が容易になります。
初心者向けの直感的な理解としては、「VAEは『元画像をうまく復元する力』と『潜在空間を標準正規分布に似せる力』をバランス良く高める」ことで、うまく学習していると言えます。
再パラメータ化トリック(Reparameterization Trick)
確率的なサンプリングは通常微分ができないため、ニューラルネットワークの学習(勾配計算)が困難です。VAEはこれを「再パラメータ化トリック」で解決します。

というサンプリングを、

と書き換えることで、εは固定した正規分布からのサンプル、μとσはネットワーク出力パラメータとして扱われ、微分可能なパスが確保されます。
これにより、バックプロパゲーションが可能になり、ニューラルネットワークのパラメータ更新が円滑に行われます。
3. VAEの数式解説
損失関数(ELBO)の詳しい説明
VAEの最終的な学習目標は、ELBOを最大化することです。
損失関数としては、ELBOにマイナスをつけたものを最小化します。

前半は再構成誤差に相当します。
これは、潜在変数 zz を用いて元の画像 xx を再構成する難しさを表します。再構成がうまくいかないほどこの項は大きくなります。後半は潜在分布が事前分布(たいていは標準正規分布)からどれだけズレているかを表します。ズレが大きいほどこの値が増え、潜在空間が複雑化してしまいます。
この項を小さくすると、潜在空間はより「シンプルで正規分布に近い」形になります。
こうして、バランス良く元データを再構成し、かつ潜在空間を整えることがVAEの学習原理です。
なぜガウス分布(正規分布)を使うのか?
ガウス分布は非常に扱いやすく、再パラメータ化トリックを適用しやすい分布だからです。また、ガウス分布は連続的で、潜在空間全体を滑らかに覆うことができるため、生成モデルとして扱いやすい特性があります。
4. VAE実装への準備
ここから実際にTensorFlow(Keras)でVAEを実装します。理論を追いかけながらプログラムコードを見ると、「なぜここで平均と分散を出しているのか?」といった疑問が解消されやすくなります。
必要なライブラリ
TensorFlow (Keras)
Matplotlib (可視化)
Numpy (数値計算)
!pip install tensorflow matplotlib
データセット準備(MNIST)
MNISTは0〜9までの手書き数字画像(28×28ピクセル)を集めた有名なデータセットです。VAEの学習例としてしばしば用いられます。
モデル設計の概要
エンコーダ:
入力画像(28×28)をベクトル化(784次元)し、全結合層や畳み込み層で潜在次元(たとえば20次元)の「平均」と「分散(あるいはlog var)」を出力します。デコーダ:
潜在変数 z を入力し、元の28×28画像を再構成するネットワークです。
5. VAEのTensorFlow実装(ステップバイステップ)
以下は標準的なVAEの実装例です。初学者向けに、なるべくシンプルな全結合層のみで構築します。
import tensorflow as tf
from tensorflow.keras import layers, Model
import numpy as np
import matplotlib.pyplot as plt
# MNISTデータ準備
(x_train, _), (x_test, _) = tf.keras.datasets.mnist.load_data()
x_train = x_train.astype('float32') / 255.0
x_test = x_test.astype('float32') / 255.0
# 28x28を784次元ベクトル化
x_train = x_train.reshape(-1, 784)
x_test = x_test.reshape(-1, 784)
latent_dim = 20
hidden_dim = 400
# エンコーダモデル定義
class Encoder(Model):
def __init__(self, latent_dim=20, hidden_dim=400):
super(Encoder, self).__init__()
self.fc1 = layers.Dense(hidden_dim, activation='relu')
self.fc_mu = layers.Dense(latent_dim) # 平均
self.fc_logvar = layers.Dense(latent_dim) # log(var)
def call(self, x):
h = self.fc1(x)
mu = self.fc_mu(h)
logvar = self.fc_logvar(h)
return mu, logvar
# デコーダモデル定義
class Decoder(Model):
def __init__(self, latent_dim=20, hidden_dim=400):
super(Decoder, self).__init__()
self.fc1 = layers.Dense(hidden_dim, activation='relu')
self.fc2 = layers.Dense(784, activation='sigmoid')
def call(self, z):
h = self.fc1(z)
x_recon = self.fc2(h) # 再構成された画像
return x_recon
encoder = Encoder(latent_dim, hidden_dim)
decoder = Decoder(latent_dim, hidden_dim)
# 再パラメータ化トリック
def reparameterize(mu, logvar):
epsilon = tf.random.normal(shape=tf.shape(mu))
z = mu + tf.exp(0.5 * logvar) * epsilon
return z
# ELBO損失関数の定義
def vae_loss(x, x_recon, mu, logvar):
# 再構成誤差: BCE
# 入力xと出力x_reconは[batch, 784]で表される0~1値の画像ピクセル
bce = tf.reduce_sum(tf.keras.losses.binary_crossentropy(x, x_recon), axis=1)
# KLダイバージェンス
kl = 0.5 * tf.reduce_sum(tf.exp(logvar) + tf.square(mu) - 1.0 - logvar, axis=1)
return tf.reduce_mean(bce + kl)
optimizer = tf.keras.optimizers.Adam(learning_rate=1e-3)
epochs = 10
batch_size = 128
train_dataset = tf.data.Dataset.from_tensor_slices(x_train).shuffle(10000).batch(batch_size)
for epoch in range(1, epochs+1):
total_loss = 0
count = 0
for batch_x in train_dataset:
with tf.GradientTape() as tape:
mu, logvar = encoder(batch_x)
z = reparameterize(mu, logvar)
x_recon = decoder(z)
loss = vae_loss(batch_x, x_recon, mu, logvar)
grads = tape.gradient(loss, encoder.trainable_variables + decoder.trainable_variables)
optimizer.apply_gradients(zip(grads, encoder.trainable_variables + decoder.trainable_variables))
total_loss += loss.numpy()
count += 1
avg_loss = total_loss / count
print(f'Epoch {epoch}, Loss: {avg_loss:.4f}')
上記のコードでは、エンコーダとデコーダを定義し、ELBOに対応する損失関数を実装しています。学習が進むと、VAEは再構成がうまくなり、潜在分布が標準正規分布に近づいていきます。
6. 学習結果の可視化と検証
再構成画像の表示
学習後、元画像と再構成画像を比較してみましょう。
# 再構成の例
x_sample = x_test[:10]
mu, logvar = encoder(x_sample)
z = reparameterize(mu, logvar)
x_recon = decoder(z)
fig, axes = plt.subplots(2, 10, figsize=(20,4))
for i in range(10):
axes[0,i].imshow(x_sample[i].reshape(28,28), cmap='gray')
axes[0,i].axis('off')
axes[1,i].imshow(x_recon[i].numpy().reshape(28,28), cmap='gray')
axes[1,i].axis('off')
plt.show()
図1:再構成画像例
上段が元のMNIST画像、下段がVAEによる再構成画像です。初期段階や学習が浅い場合は再構成がぼやけるかもしれませんが、訓練を重ねればよりクリアな数字が再現されるようになります。これにより、潜在空間が入力データの特徴を的確に捉えていることがわかります。
潜在空間の2次元可視化(例)
latent_dimを2にすれば、潜在空間を直接2次元にプロットできます。ここでは例として、latent_dim=2で学習し直した場合を想定しましょう(上記コードではlatent_dim=20ですが、理解のための参考例です)。
# latent_dim=2の場合の参考例(学習済みと仮定)
# mu, logvar = encoder_2d(x_test) # encoder_2dはlatent_dim=2で構築した仮のモデル
# z = mu
# y_test = ... # ラベルを取得できる場合
# plt.figure(figsize=(8,6))
# plt.scatter(z[:,0].numpy(), z[:,1].numpy(), c=y_test, cmap='tab10')
# plt.colorbar()
# plt.xlabel('z1')
# plt.ylabel('z2')
# plt.title('Latent Space Visualization')
# plt.show()
このような図では、似たような数字同士が近い場所に集まる傾向があり、潜在空間がデータの特徴量を効果的に圧縮・組織化している様子が視覚的に確認できます。
潜在変数からの新規サンプル生成
潜在空間が正規分布に従うようになったため、ランダムに潜在変数をサンプリングして新たな画像を生成できます。
z_samples = tf.random.normal(shape=(64, latent_dim)) # 標準正規分布から潜在変数をサンプル
generated = decoder(z_samples)
fig, axes = plt.subplots(8,8, figsize=(8,8))
for i in range(8):
for j in range(8):
axes[i,j].imshow(generated[i*8+j].numpy().reshape(28,28), cmap='gray')
axes[i,j].axis('off')
plt.show()
図2:ランダム生成サンプル例
ここでは、まだ見たことがない新たな手書き数字が潜在空間から生成されます。数字らしくないものが混じる場合もありますが、学習が十分であれば多くは「それらしい」数字が生成されます。これがVAEの「生成モデル」としての強みです。
7. 応用例とサービス化へのヒント
VAEは単純な再構成や生成以上の応用が可能です。
データ拡張:
潜在空間から多様なサンプルを生成し、学習データを増やすことで、他のモデル(例えば分類器)の精度向上に活かせます。異常検知:
正常データのみでVAEを学習した後、異常なデータを入力すると再構成誤差が大きくなります。これを基準に異常検知システムを構築できます。潜在空間による検索・生成サービス:
潜在空間は「データの本質的な特徴」を低次元で捉えているため、似たデータの検索や、潜在変数操作による特徴操作(例えば「数字の太さ」を連続的に変える)といった応用が可能です。関連モデルへの拡張:
CVAE(Conditional VAE):クラスラベルなどの条件を与えることで、特定クラスのデータを生成可能。
Beta-VAE:潜在空間の独立性を強化し、より解釈可能な特徴表現を得る手法。
こうした発展モデルや応用アイデアにより、VAEは新しいサービス開発の強力な基盤となり得ます。理解を深めた上で、自分独自の発想で潜在空間を利用することで、オリジナルな生成サービスや分析ツールを生み出せる可能性があります。
8. まとめと今後の学習指針
本記事では、変分オートエンコーダ(VAE)の理論的基礎からTensorFlow実装、可視化までを丁寧に解説しました。ポイントは以下の通りです。
理論面:
潜在変数モデルとしてのVAEは、エビデンス下界(ELBO)を最大化しながら、「再構成の上手さ」と「潜在分布の規則性」を両立させます。再パラメータ化トリックにより、勾配計算が可能になり学習が実現されます。実装面:
TensorFlowを用いてエンコーダ、デコーダを定義し、ELBOに対応する損失関数を実装しました。MNISTを例に、学習経過を観察し、再構成画像やサンプル生成が正しく行われることを確認しました。応用面:
データ生成、データ拡張、異常検知など、多岐にわたる応用が可能であり、サービス開発のアイデアも得られます。また、CVAEやBeta-VAEなど、VAEを発展させた手法にも踏み出せます。
この記事を一通りマスターすると、VAEをゼロから理解し、実際に動かしてみることで確固たる基礎を築くことができます。これは他の高度な生成モデル(GANや拡散モデル)を学習する上での土台にもなります。ぜひ、学んだ知識を応用して、独自のサービスや分析手法を開発してみてください。
(以上)
