鳳南におけるプレイヤー実力分布の推定 (Re: ルールによる実力の出やすさの違い)

概要

各順位の獲得回数データをもとに「母集団の実力の分布」を推定する。

背景

[chanpukin2021]: ルールによる実力の出やすさの違い の一部を追試する。

[chanpukin2021] には鳳南における平均獲得ptの分布 (各順位の獲得回数をもとに七段配分で算出したもの、500戦以上) が掲載され「実際の (実力) 分布より少し広がっています」とある。その補正として「実力分布の事前分布を仮定し、事後分布を足し上げる」という方法がとられているが「事前分布の妥当性が難しく、そもそも母集団の分布を求めるのに事前分布ってなんだ? って感じになりました」と課題が残っていた。

問題は 推定するべき事前分布そのものを仮定してしまった ことである。事前分布による仮定は普通、推定するべき分布のパラメータに対しておこなう。つまり実力分布を推定するにあたっては平均と標準偏差を任意とした正規分布を仮定するのではなく、たとえば平均 0, 標準偏差 σ の正規分布を仮定し、標準偏差 σ が何らかの事前分布にしたがう (もしくは σ については何もわからない) とする。

なお [chanpukin2021] の結論の妥当性は本実験によって肯定/否定されものではない。実力分布推定の部分は良くない仮定によっているが「事前分布の分散を少し色々いじってみても後々重要となる標準偏差の比はあまり変わりませんでした」とのことである。

以下では上述のように「実力分布は 平均 0, 標準偏差 σ の正規分布であると仮定し、標準偏差 σ を推定する」ことをおこなう。

結果

読者の大半は結果にしか (もしかしたら、結果にすら) 興味がないだろうから結果をあらわすチャートをいくつか掲載するにとどめる。購入者にはコードなども共有する用意がある。

基礎的な分布

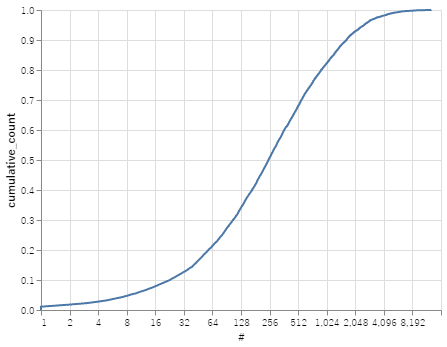
まず打数の累積分布を観察した。

次に打数を制限せずに平均獲得ptとの関係をプロットした。左が平方根スケール、右が対数スケール。平均獲得pt は (正負あるため) 線型にしたのであまり見やすくなかった。

モデルの仮定に基づく確率の計算

獲得pt が正規分布で近似できると仮定したモデル (normal) と順位獲得確率が線型 (各順位の獲得率が等差数列で表される) と仮定したモデル (linear) とを構築した。実力分布の標準偏差として 1 および 2 を仮定したとき、各プレイヤーのプレイ結果が現れる確率のようなものを計算した。

それぞれのモデルを固定すると、標準偏差を変えても「確率のようなもの」に強い相関がみられた。左下に向かって広がっていくのは「多くの対局をこなすと、平均から離れた実力をもつプレイヤーの結果が偶然だけでは説明できなくなる」現象といえるはずだ。

一方、標準偏差をそれぞれ固定すると linear と normal との相関は逆のように見えた。これには (理由は省略) 試合数が関係していると考えられた。

試合数の少ない (less: 32..64) または多い (1024..2048) プレイヤーの結果のみをプロットしてみるとこれが確かめられた。

結論

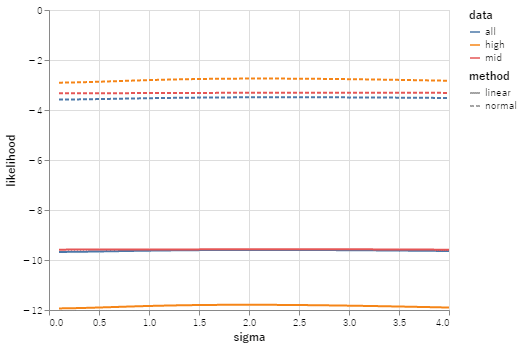
試合数の制限 (mid: 中位半分、all: 正のものすべて、high: 上位半分) とモデルの組み合わせ6種類について、標準偏差を変えてデータ全体が得られる「確率のようなもの」をプロットしてみたところ、細かくてよくわからないが実験した範囲で最大をとっているようだった。

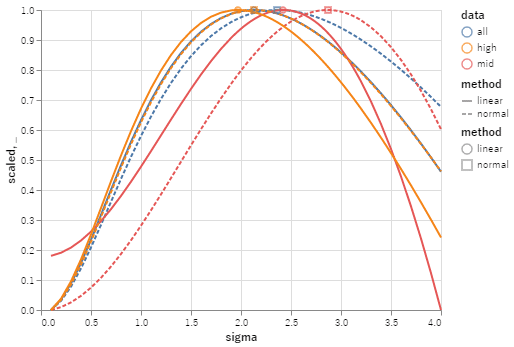
スケールを変えて見やすくし、最大をとった点を打った。

実力分布の標準偏差として尤度を最大にする値は 1.97–2.87, 6つの結果のうち最小と最大を除くと 2.13–2.42 であった。試合数は多いほど推定値は小さく (high < all < mid), 同じデータでは順位獲得確率分布が線型であるモデルより獲得報酬が正規分布である近似モデルのほうが推定値が大きく (linear < normal) なった。

順位評価による表示および過去文献との比較 (訂正あり) (追記あり)

次の2パラグラフに誤りを含んでいたので訂正してある:『科学する麻雀』の実力分布標準偏差はランキング超上級卓ではなく東風荘全体を対象としたものらしい。であれば 4.9倍の開きは選抜の結果であるとして納得のいくものである。これは私の誤読によるもので、個人的な理由で十分な確認ができなかったまま「適切でなかった可能性がある」と書いたことについて、とつげき東北さまに説明しお詫びした。

ここまでの実験は鳳南七段の順位獲得回数データおよび報酬をベースに行った。この結果を雑に換算すると順位にして 0.0305 程度となった。一方『科学する麻雀』[とつげき東北2004] には「(訂正済: 東風荘) における実力分布標準偏差は平均順位にして 0.15 程度」とある。単純には約4.9倍の開きがある。この要因として次のような点が考えられる:

1. (削除)
2. (訂正済: 東風荘全体) に比べて鳳南には厳しい選抜がはたらいている

既知の誤りを含む部分おわり

さらに追記はじまり

[とつげき東北2004] には「ランキング超上級卓」の実力分布についての情報も掲載されていた。

また、「東風荘」には「超上級卓」という名称の、一定以上の成績の人しか打てない卓がある。これは「通常卓」において、およそ2.2位より高い成績をある程度の期間 (数百試合) キープしている人だけが参加できる卓であり、かなり選抜された空間である。この「超上級卓」内部での実力の分布を調べたところ、標準偏差は東風戦で 0.0520位, 東南戦で0.0569位であった。

天鳳における選抜は段位とレーティングとの2つの要素からなるが、それぞれで比較してみる。まず段位 (七段) については、六段配分で期待ポイントが正になる順位分布と思うと上卓で 23:20:17:14 より優れているということになる (天鳳のプレイヤーは基本的に上卓には到達することができると考え、東風荘の通常卓と対応するとした) ので、平均順位にして2.3程度 (2.2̇97̇)。次にレーティング (2000) について、天鳳ではR800が平均順位1に相当するから、上卓の平均Rを1600程度 (1級から三段までの平均Rと在位数から計算) として 2.5-(2000-1600)/800 = 2.0程度。鳳凰卓でプレイするにはこれらを両方みたす必要があるから、東風荘における超上級ランキング卓への選抜より厳しいと考えられる。これは [とつげき東北2004] の結果 (超上級卓での実力分布標準偏差は、この実験で求めた値より大きい) と整合する。

さらに追記おわり

今後の課題

いくつか本実験で考慮できなかった課題がある。

1. 実力分布の仮定が狭い: 平均が 0 とは限らない正規分布または他の分布についても実験すること
2. 生存バイアスを考慮していない: [chanpukin2021] も触れているように「弱いと打ち続けることができない」ことを打数が実力または結果に依存するモデルを構築すること
3. 対戦相手を考慮していない: たまたま対戦相手が強い/弱いことによる成績への影響を考慮すること
3a. 簡単には、対戦相手の実力のモデルは単純な正規分布とし、結果の分布がそれに線型に依存するモデルでよいと思われる
3b. より厳密には、対戦相手の実力分布・対戦相手の実力と結果分布との関係 をモデル化する
4. 実力の変化を考慮していない: これはもうなんとかするつもりはない

今後の課題 (追加)

とつげき東北氏とやや話が噛み合っていなかったが、このツイート後半について DM で具体的に教えていただいた。

母集団内部の分布の推定ですか？私は
・東風荘で公開されている十分に大きな量のデータで正規分布近似できることを確認しています
・超ラン（懐かしいｗ）と上ランの接続付近では、当然断絶が生じる（ちょうど試験のギリギリ合格と不合格みたいに）
これに理屈や式をそれなりに当てて納得できます。

— とつげき東北🌘 (@totutohoku) February 10, 2021

課題2には「弱いと打ち続けることができない」と書いたが、鳳南はプレイ前に特上卓という異なる場での結果に基づいた選抜が行われた空間である。したがって選抜前の実力分布や選抜の構造も仮定または推定対象に含めることで分析を改善する余地がある。